
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операції над прямокутними матрицями.Содержание книги
Поиск на нашем сайте
Розглянемо прямокутні матриці. З’ясуємо за яких умов операції над прямокутними матрицями можна здійснювати за тими ж правилами, що й над квадратними. Почнемо з прикладів:
Проаналізувавши наведені приклади, приходимо до такого правила множення прямокутних матриць. Правило: Дві прямокутні матриці можна перемножити, якщо кількість елементів в рядку першої матриці збігається з кількістю елементів в стовпці другої матриці, тобто кількість столбців першої матриці дорівнює кількості рядків другої матриці, причому добуток має стільки рядків, скільки їх в першій матриці, і стільки стовпців, скільки їх в другій матриці.
Властивості прямокутних матриць. 1. Множення прямокутних матриць не комутативне. 2. Множення трьох матриць (якщо їх можна перемножити), підпорядковується асоцітивному закону, тобто (АВ)С = А(ВС). Доведення таке саме, як для квадратних матриць.
Розглянемо тепер і множення прямокутних матриць на число. Аналізуючи операцію додавання квадратних матриць, приходимо до висновку, що додавати можна матриці однакових розмірів. А множити на число можна будь-яку матрицю. Так само, як для квадратних матриць можна довести, що множина всіх прямокутних матриць одного розміру (s´n) є векторним простором відносно операцій додавання і множення матриці на число. Причому, арифметичним простором вимірності (s´n). Так само, як для квадратних матриць, можна вказати базіс простору. Ці матриці мають нульові єлементи, крім одного. Цей єлемент є 1. Таких матриць (s´n). Псевдообернені матриці. Почнемо з інформації про ранг добутку матриць, яка виявиться корисною при з’ясуванні умов існування псевдообернених матриць. Відмітемо без доведення теорему. Теорема. Ранг добутку матриць А і В не перевищує ранг матриці А і ранг матриці В. Для подальшого важливим є наслідок з наведеної теореми. Наслідок. Ранг добутку двох матриць А і В, з яких одна, наприклад В, невироджена, дорівнює рангу матриці А. Доведення. Нехай С = А × В, det B ¹ 0. (1) Треба довести, що r C = r A. З теореми випливає, що r C £ r A, (2) з того, що det B¹0, випливає, що існує матриця rA£ rC (3) З (2) та (3) випливає, що r А = r С.
Нехай задано прямокутну матрицю А=(
Означення. Матриця, що умовно позначається
Аналогічно вводиться поняття псевдооберненої правої матриці, якщо вона задовольняє умові: А× Для того, щоб з¢ясувати умови існування псевдообернених матриць, треба розподілити всі прямокутні матриці на два класи: горизонтальні та вертикальні. Означення. Матриця називається горизонтальною, якщо кількість рядків в ній менша за кількість стовпців. Матриця називається вертикальною, якщо кількість стовпців в ній менша за кількість рядків. Теорема 1. Жодна горизонтальна матриця немає псевдооберненої лівої. Доведення. Нехай матриця А – горизонтальна матриця, тобто s<n. Тоді за означенням виконується рівність n =r E £ r A £ s, n £ s, що суперечить умові. Так само може бути доведено теорему 1¢. Теорема 1¢. Жодна вертикальна матриця не має оберненої правої. Для того, щоб з¢ясувати, за яких умов горизонтальна матриця має праву, а вертикальна – псевдообернену ліву, треба ввести поняття рядковоневиродженної і стовпцевоневиродженної матриць.
Означення. Матриця називається рядкововиродженною, якщо її стовпці утворюють лінійнонезалежну систему. Матриця називається стовпцовоневиродженною, якщо її стовпці утворюют лінійнонезалежну систему. З цього означення випливає, що горизонтальна матриця не може бути стовпцевоневиродженною, а вертикальна – рядковоневиродженною. Теорема 2. Для того, щоб матриця мала псевдообернену праву, необхідно і достатньо, щоб вона була рядкововиродженною. Доведення. Небхідність. Нехай матриця А має псевдообернену праву. Треба довести, що матриця А – рядковоневиродженна, тобто r A = s. З того, що існує Достатність. Нехай матриця А – рядкововиродженна (r A = s). Треба довести, що існує Як відомо для можливості множення матриця Е має бути (s×s), а тоді Х має бути (n×s).
Отже матриця Х задовольняє умову:
Безпосереднім множенням знайдемо елементи першого рядка добутку матриць
Треба довести, що система (5) сумісна. Для цього треба довести, що виконуються умови теореми Кронекера-Капеллі:
За умовою теореми rA = s. Ранг r Таким чином, виконується теорема Кронекера-Капеллі. Система (2) сумісна. Розв¢язавши її, знайдемо перший стовпчик шуканої матриці Х. Більш того, зауважемо, що система (2) має безліч розв¢язків. Оскільки r A = s < n, то виконуються умови критерія невизначеності. Так само отримаємо систему рівнянь, що містить другий стовпчик матриці Х:
Так само доведемо, що система сумісна. Поступаючи аналогічним чином, отримаємо систему для останнього стовпця матриці Х. Отже доведено, що існує псевдообернена права матриця Х для матриці А. Більш того, вона не єдина, їх безліч. Комплесні числа.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.006 с.) |

 - таке множення не можливо.
- таке множення не можливо. ,
,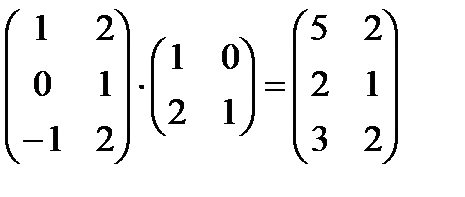 ,
,  .
. . П омножимо обидві частини рівності на
. П омножимо обидві частини рівності на  ), розміру s´n,
), розміру s´n,
 , називається псевдооберненою лівою, якщо вона задовольняє умові:
, називається псевдооберненою лівою, якщо вона задовольняє умові: ×А=Е.
×А=Е. =Е.
=Е. × А = Е. В матриці Е повинно бути стільки стовпців, скільки в матриці А, тобто квадратна матриця Е має розмір n´n. Ранг матриці Е дорівнює n, тому що в ній є мінор n-го порядку, що не дорівнює нулю. З іншого боку, застосуємо теорему про ранг добутку двох матриць.
× А = Е. В матриці Е повинно бути стільки стовпців, скільки в матриці А, тобто квадратна матриця Е має розмір n´n. Ранг матриці Е дорівнює n, тому що в ній є мінор n-го порядку, що не дорівнює нулю. З іншого боку, застосуємо теорему про ранг добутку двох матриць. , випливає А ×
, випливає А ×  = Е (s´s). З цього випливає, що rE=s. З теореми про ранг добутку матриць s = r E £ r A £ s. Тобто r A = s.
= Е (s´s). З цього випливає, що rE=s. З теореми про ранг добутку матриць s = r E £ r A £ s. Тобто r A = s. . Для цього з’ясуємо, чи існує така матриця Х, що А × Х = Е.
. Для цього з’ясуємо, чи існує така матриця Х, що А × Х = Е.
 . (4)
. (4)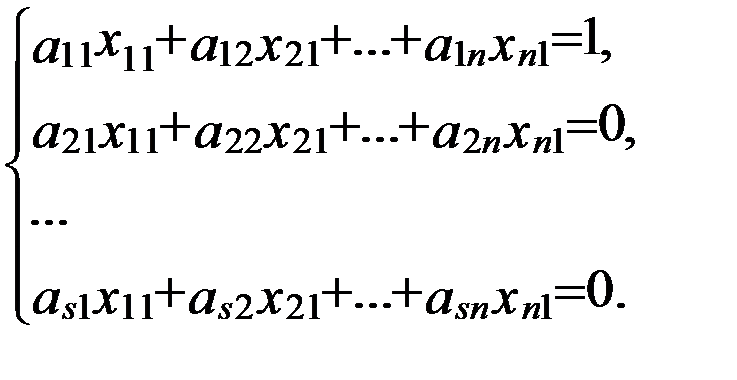 (5)
(5)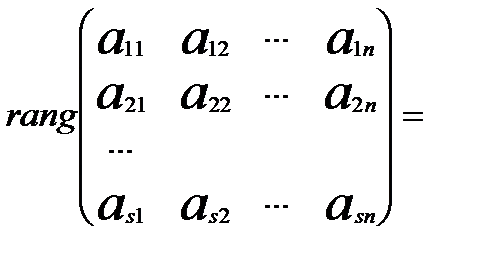
 .
. також дорівнює s, тому що вона містить мінор s- го порядку, що не дорівнює нулю. Це мінор матриці А, а мінорів більш вищого порядку для
також дорівнює s, тому що вона містить мінор s- го порядку, що не дорівнює нулю. Це мінор матриці А, а мінорів більш вищого порядку для 



