
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Системы линейных уравнений (основные алгоритмы)Содержание книги Поиск на нашем сайте
1. Сколько решений имеет система уравнений А) Система имеет единственное решение. Б) Система имеет три решения. В) Система имеет бесконечное множество решений. Г) Система несовместна.
2. Сколько решений имеет система уравнений А) Система имеет единственное решение. Б) Система имеет три решения. В) Система имеет бесконечное множество решений. Г) Система несовместна.
3. Матрица системы линейных уравнений имеет вид А) Система приведена к ступенчатому виду. Б) Система совместна и определена. В) Система несовместна. Г) Четвертое уравнение системы противоречиво.
4. Матрица системы линейных уравнений имеет вид А) Система не приведена к ступенчатому виду. Б) Система совместна и определена. В) Система несовместна. Г) Четвертое уравнение системы противоречиво.
5. Матрица системы линейных уравнений имеет вид А) Система имеет единственное решение (1, 1, 1, 1). Б) Система имеет три главных и одно свободное неизвестное. В) Система неопределенна, ее решение зависит от двух свободных неизвестных. Г) Система приведена к треугольному виду и поэтому имеет единственное решение.
6. Матрица системы линейных уравнений имеет вид А) Система имеет три главных и одно свободное неизвестное. Б) Система неопределенна, ее решение зависит от двух свободных неизвестных. В) Система имеет единственное решение (1, 1, 1, 1). Г) Система приведена к треугольному виду и поэтому имеет единственное решение.
7. Матрица системы линейных уравнений имеет вид А) При любом значении а система совместна. Б) При любом а ≠ 0 система совместна. В) При любом значении а система несовместна. Г) При любом а ≠ 1 система совместна и неопределена.
8. Расширенная матрица системы линейных уравнений имеет вид А) При любом значении а система совместна. Б) При любом а ≠ 0 система совместна. В) При любом а ≠ 4 система совместна и неопределенная. Г) При любом значении а система несовместна.
9. Укажите неверное утверждение относительно системы однородных уравнений, матрица которой имеет вид А) Система совместна, неопределенная, имеет множество решений:
Б) Все решения системы пропорциональны. В) Существует хотя бы два непропорциональных решения системы. Г) Система совместна, неопределенная, имеет множество решений:
10. Укажите неверное утверждение относительно системы линейных уравнений, матрица которой имеет вид А) Система совместна и имеет конечное множество решений. Б) Система совместна и имеет бесконечное множество решений. В) Система несовместна. Г) Система имеет единственное решение.
11. Для системы линейных уравнений, заданной матрицей А) (2, 4, 1); Б) (1, 2, 4); В) (4, 2, 1); Г) (4, 1, 2).
12. Две системы линейных уравнений заданы матрицами
А) Системы равносильны. Б) Системы несовместны. В) Системы не равносильны. Г) Ранг основной матрицы первой системы меньше ранга основной матрицы второй системы.
13. Тройка чисел (2, 0, –1) является решением системы: А) Б) В) Г)
14. Тройка чисел (1, –1, 2) является решением системы: А) Б) В) Г)
15. Укажите верное утверждение относительно системы линейных уравнений, матрица которой имеет вид А) Система совместна и имеет единственное решение (0, Б) Система совместна и имеет бесконечное множество решений. В) Система несовместна. Г) Система имеет единственное решение (0, 0).
16. Система линейных уравнений задана матрицей А) Набор (–1, 2, 1) является решением системы. Б) Система имеет два решения (–1, 2, 1) и (3, 0, 6). В) Система несовместна. Г) Набор (1, 1, 2) является решением системы.
17. Укажите систему линейных уравнений, не равносильную системе А) Б) В) Г)
Тема 5. Матрицы и определители (Основные понятия) 1. Рангом матрицы называется: А) число строк матрицы; Б) число столбцов матрицы; В) число ненулевых элементов матрицы; Г) максимальное число линейно независимых строк матрицы.
2. Укажите матрицу, которая является единичной: А) Б) В) Г)
3. Квадратная матрица называется вырожденной, если: А) число строк матрицы равно числу столбцов; Б) число столбцов матрицы меньше числа строк; В) ранг матрицы меньше ее порядка; Г) ранг системы столбцов матрицы равен рангу системы строк.
4. Квадратная матрица A называется обратимой, если существует такая матрица B, что: А) Б) В) Г)
5. Квадратная матрица называется невырожденной, если: А) число строк матрицы равно числу столбцов; Б) число столбцов матрицы меньше числа строк; В) ранг системы столбцов матрицы не равен рангу системы строк; Г) ранг матрицы равен ее порядку.
6. Укажите симметрическую матрицу: А) Б) В) Г)
7. Квадратная матрица называется диагональной, если: А) равны элементы матрицы, симметричные относительно главной диагонали; Б) все элементы матрицы, кроме элементов главной диагонали, равны нулю; В) все элементы матрицы, находящиеся под главной диагональю, равны нулю; Г) все элементы матрицы, находящиеся на главной диагонали, равны нулю.
8. Определителем квадратной матрицы называется: А) алгебраическая сумма n! слагаемых, каждое из которых есть произведение n сомножителей, взятых из каждой строки и каждого столбца со знаком «+», или со знаком «–»; Б) алгебраическая сумма n! слагаемых, каждое из которых есть произведение n сомножителей, взятых точно по одному из каждой строки и каждого столбца, со знаком «+», если подстановка от номеров строк к номерам столбцов выбранных элементов четная, и со знаком «–», если эта подстановка нечетная; В) произведение n сомножителей, взятых точно по одному из каждой строки и каждого столбца со знаком «+», если подстановка от номеров строк к номерам столбцов выбранных элементов четная, и со знаком «–», если эта подстановка нечетная; Г) алгебраическая сумма n! слагаемых, взятых точно по одному из каждой строки и каждого столбца со знаком «+», если подстановка от номеров строк к номерам столбцов выбранных элементов четная, и со знаком «–», если эта подстановка нечетная.
9. Минором элемента aij квадратной матрицы А называется определитель матрицы, полученной из исходной: А) перестановкой i -й строки и j -го столбца; Б) вычеркиванием i -й строки и j -го столбца; В) вычеркиванием j -й строки и i -го столбца; Г) умножением на элемент aij всех элементов i -й строки.
10. Алгебраическим дополнением элемента aij квадратной матрицы А называется: А) минор Mij элемента aij с противоположным знаком; Б) минор Mij элемента aij, умноженный на элемент aij; В) минор Mji элемента aji, умноженный на элемент aij; Г) минор Mij элемента aij, умноженный на (–1) i+j. 11. Матрицу А можно умножить на матрицу В, если: А) число строк матрицы А равно числу строк матрицы В; Б) число столбцов матрицы А равно числу столбцов матрицы В; В) число столбцов матрицы А равно числу строк матрицы В; Г) число строк матрицы А равно числу столбцов матрицы В.
12. Матрица А имеет обратную матрицу, если матрица А: А) вырожденная; Б) невырожденная; В) имеет определитель, равный 0; Г) имеет две пропорциональные строки.
13. Укажите верное высказывание: А) если АВ=ВА, то А и В – квадратные матрицы одинаковых размеров; Б) если АВ и ВА существуют, то А и В – квадратные матрицы; В) если АВ и ВА существуют, то АВ = ВА; Г) если А – квадратная матрица и АВ существует, то и В – квадратная матрица.
14. Укажите неверное высказывание о матричном равенстве АВ=С: А) система столбцов матрицы С линейно выражается через систему столбцов матрицы А; Б) система строк матрицы С линейно выражается через систему строк матрицы В; В) ранг матрицы С не меньше рангов матриц А и В; Г) если С – нулевая матрица и А – невырожденная квадратная матрица, то В – нулевая матрица.
15. Даны матричные уравнения AX=B (1) и YA=B (2). Укажите неверное высказывание: А) если А и В имеют разное число строк, то уравнение (1) неразрешимо; Б) если ранг А меньше ранга В, то оба уравнения неразрешимы; В) если матрица А невырожденная, то уравнения (1) и (2) имеют более, чем по одному решению; Г) если уравнения (1) и (2) разрешимы одновременно, то их решения X и Y – квадратные матрицы.
16. Укажите верное утверждение: А) умножение квадратных матриц одного порядка коммутативно; Б) умножение матриц ассоциативно; В) сложение квадратных матриц одного порядка не ассоциативно; Г) сложение квадратных матриц одного порядка не коммутативно.
17. Укажите верное утверждение: А) при умножении матрицы на число ее ранг изменится на это число; Б) ранг системы строк матрицы не всегда равен рангу системы столбцов этой же матрицы; В) элементарные преобразования системы столбцов изменяют строчный ранг матрицы; Г) если к одной из строк матрицы прибавить другую, умноженную на любое число, то ранг матрицы не изменится.
18. Определители квадратной матрицы А и транспонированной матрицы АT: А) равны; Б) имеют противоположный знак; В) в произведении дают 1; Г) в произведении дают –1.
19. Определитель вырожденной матрицы равен: А) 1; Б) –1; В) 0; Г) любому действительному числу.
20. Определитель матрицы не изменится, если: А) к одной строке определителя прибавить его другую строку; Б) две строки определителя поменять местами; В) один из столбцов определителя умножить на 2; Г) два столбца определителя поменять местами.
21. Определитель диагональной матрицы равен: А) 0; Б) произведению элементов ее главной диагонали; В) сумме квадратов элементов этой матрицы; Г) сумме элементов ее главной диагонали.
22. Определитель треугольной матрицы равен: А) 0; Б) 1; В) произведению элементов ее главной диагонали; Г) сумме элементов ее главной диагонали.
23. При перестановке двух столбцов (строк) матрицы ее определитель: А) не изменяется; Б) меняет знак; В) становится равным нулю; Г) увеличивается на 1.
24. Если все элементы какой либо строки (столбца) матрицы умножить на число a ¹ 0, то определитель этой матрицы: А) не изменится; Б) увеличится на а; В) изменится в а раз; Г) станет равным нулю.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.148 (0.007 с.) |

 ?
? ?
? . Укажите верное утверждение.
. Укажите верное утверждение. . Укажите верное утверждение.
. Укажите верное утверждение. . Укажите верное утверждение.
. Укажите верное утверждение. . Укажите верное утверждение.
. Укажите верное утверждение. . Укажите верное утверждение.
. Укажите верное утверждение. . Укажите верное утверждение.
. Укажите верное утверждение.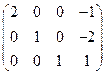 .
. .
. .
. .
. , решением является набор чисел:
, решением является набор чисел: и
и . Укажите верное высказывание.
. Укажите верное высказывание. ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. .
. ).
). . Укажите верное высказывание.
. Укажите верное высказывание. :
: ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. ;
;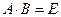 и
и  ;
;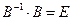 ;
;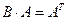 .
.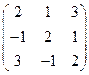 ;
; ;
; ;
; .
.


