
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Матрицы и определители (основные алгоритмы)Содержание книги Поиск на нашем сайте
1. Найдите ранг матрицы А) 3; Б) 4; В) 1; Г) 2. 2. Найдите произведение матрицы А) Б) В) Г)
3. Найдите произведение матрицы А) Б) В) Г) 4. Найдите сумму матриц А) Б) В) Г)
5. Для матрицы А) Б) В) Г)
6. Вычислите А) Б) В) Г) нельзя выполнить действия.
7. Решите матричное уравнение А) Б) В) Г) нет решений.
8. Решите матричное уравнение А) Нет решений; Б) В) Г)
9. Найдите сумму матриц А) Б) В) Г)
10. Для матрицы А) Б) В) Г)
11. Найдите произведение матрицы А) Б) В) Г)
12. Для матрицы А) Б) В) Г)
13. Найдите матрицу, обратную для матрицы А) Б) В) Г)
14. Найдите сумму матриц А) Б) В) Г)
15. Для матрицы А) Б) В) Г)
16. Найдите произведение матрицы А) Б) В) Г) нельзя выполнить действие.
17. Найдите произведение матрицы А) Б) В) Г)
18. Найдите разность матриц А) Б) В) Г)
19. Найдите ранг матрицы А) 1; Б) 2; В) 3; Г) 4.
20. Найдите ранг матрицы А) 1; Б) 2; В) 3; Г) 4.
21. Вычислите определитель А) 0; Б) –5; В) 5; Г) 71. 22. Вычислите определитель А) 0; Б) 48; В) 6; Г) –24.
23. Вычислите определитель А) –12; Б) 12; В) 20; Г) –20.
24. Найдите минор элемента a 41определителя А) 0; Б) 4; В) –7; Г) 7.
25. Найдите алгебраическое дополнение элемента a 41определителя
А) 0; Б) 4; В) –7; Г) 7.
26. Вычислите определитель А) 0; Б) 3; В) –21; Г) 21.
27. Вычислите определитель А) 4; Б) 0; В) –4; Г) другой ответ.
28. Вычислите определитель А) 0; Б) –21; В) 21; Г) 14.
29. Вычислите определитель А) 0; Б) 1; В) 12; Г) –12.
30. Вычислите определитель А) 0; Б) 1; В) –1; Г) другой ответ.
31. Вычислите определитель А) 0; Б) 1; В) 5; Г) 3.
32. Найдите минор элемента a 32 определителя А) 0; Б) –7; В) 7; Г) 5.
33. Найдите алгебраическое дополнение элемента a 32 определителя
А) –7; Б) 7; В) 0; Г) 5.
34. Найдите минор элемента a 23определителя А) 0; Б) –8; В) 8; Г) 4.
35. Найдите алгебраическое дополнение элемента a 23определителя
А) 0; Б) –8; В) 4; Г) 8.
36. Найдите минор элемента a 44определителя А) 12; Б) 0; В) –4; Г) 4.
37. Найдите алгебраическое дополнение элемента a 44определителя
А) 12; Б) 0; В) –12; Г) 4.
38. Найдите минор элемента a 23определителя А) 0; Б) –3; В) 3; Г) 6.
39. Найдите алгебраическое дополнение элемента a 23определителя
А) 0; Б) 6; В) –3; Г) 3. 40. Вычислите определитель А) 0; Б) 1; В) 8; Г) –3.
Тема 7. векторные ПРОСТРАНСТВА (Основные понятия)
1. Какие из следующих множеств чисел с обычными операциями сложения и умножения являются линейными пространствами над полем Q? А) N, Z, Q; Б) Z, R, C; В) Z, Q, R; Г) Q, R, C.
2. Следующее множество матриц с обычными операциями сложения матриц и умножения матриц на элементы поля R не является линейным пространством: А) множество всех прямоугольных матриц размерами m ´ n с действительными элементами; Б) множество всех матриц второго порядка с действительными элементами; В) множество всех матриц; Г) множество всех матриц второго порядка с комплексными элементами.
3. Множество векторов со сложением векторов и умножением вектора на действительное число, определяемых правилами векторной алгебры, не является действительным линейным пространством: А) множество всех векторов, параллельных данной прямой, проходящей через начало координат; Б) множество всех ненулевых векторов, не параллельных данной прямой; В) множество всех векторов, параллельных заданной плоскости, проходящей через начало координат; Г) множество всех векторов пространства.
4. Пусть V — пространство направленных отрезков плоскости, отложенных от начала координат (система координат декартова). Следующее множество векторов образует подпространство: А) множество всех векторов первого и второго координатных углов; Б) множество всех векторов первого и третьего координатных углов; В) множество всех векторов, лежащих на оси Ох; Г) множество всех векторов, лежащих на оси Ох или Оу.
5. Пусть V — пространство направленных отрезков плоскости, отложенных от начала координат (система координат декартова). Следующее множество векторов образует подпространство: А) линейная оболочка ненулевого вектора; Б) множество всех векторов второго и четвертого координатных углов;
В) линейное многообразие, порожденное ненулевым вектором; Г) множество всех векторов первого и четвертого координатных углов.
6. Пусть L — линейная оболочка двух непропорциональных векторов арифметического трехмерного пространства. Подпространство L изоморфно: А) R 1; Б) R 2; В) R 3 Ç R 1; Г) R 3.
7. Следующее множество с обычным сложением и умножением на число является действительным линейным пространством: А) множество всех многочленов степени n с действительными коэффициентами; Б) множество всех разрывных действительных функций на отрезке [ a; b ] с действительными коэффициентами; В) множество всех многочленов с действительными коэффициентами, степень которых не превосходит n; Г) множество всех многочленов с действительными коэффициентами, степень которых не меньше n.
8. Следующее множество векторов на декартовой плоскости, отложенных от начала координат, с обычным сложением и умножением на число является действительным линейным пространством: А) множество, состоящее из одного ненулевого вектора; Б) множество всех векторов, концы которых лежат на прямой, не проходящей через начало координат; В) множество всех векторов, лежащих на прямой, проходящей через начало координат; Г) множество всех векторов, концы которых лежат в первой или в третьей четверти.
9. Подпространством арифметического векторного пространства R А) –1; Б) 1; В) 0; Г) 2. 10. Пусть V — множество всех направленных отрезков, отложенных от начала координат. Укажите истинные утверждения. А) Линейная оболочка всякого ненулевого вектора первого координатного угла есть все векторы этого угла, включая векторы на осях. Б) Линейная оболочка двух различных ненулевых векторов из первого координатного угла есть множество всех векторов первого и третьего координатных углов. В) Линейная оболочка всякого ненулевого вектора из первого координатного угла есть все векторы верхней полуплоскости. Г) Линейная оболочка ненулевого вектора есть множество всех векторов прямой, проходящей через начало координат и имеющей направляющим вектором данный вектор.
11. Система векторов векторного пространства является его базисом, если: А) ее линейная оболочка совпадает со всем пространством. Б) данная система линейно независимая и ее линейная оболочка совпадает со всем пространством; В) данная система линейно независима; Г) всякий вектор пространства хотя бы одним образом выражается через эту систему.
12. Для любых подпространств L А) dim (L Б) dim (L В) dim (L Г) dim (L
13. В пятимерном векторном пространстве два подпространства размерностей 2 и 3 имеют пересечение размерности m. Верно, что: А) в любом случае m ≠ 0; Б) в любом случае m = 1; В) в любом случае m = 2; Г) (m = 0)
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.194 (0.008 с.) |

 .
. на матрицу
на матрицу  .
.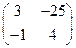 ;
;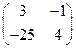 ;
; ;
;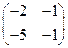 .
.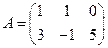 на матрицу
на матрицу  .
.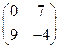 ;
; ;
; ;
; .
. и
и  .
.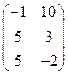 ;
; ;
;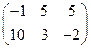 ;
; .
. найдите обратную матрицу
найдите обратную матрицу ;
;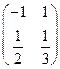 ;
;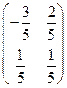 ;
; .
. , где
, где  .
.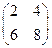 ;
; ;
;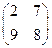 ;
;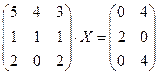 .
.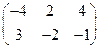 ;
; ;
;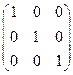 ;
;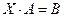 , где
, где  ,
,  .
.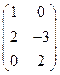 ;
; ;
; .
.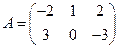 и
и  .
. ;
;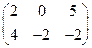 ;
;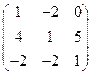 ;
;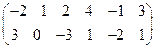 .
. найдите матрицу АТ.
найдите матрицу АТ.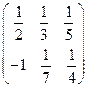 ;
; ;
; ;
;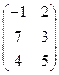 .
. на число –3.
на число –3.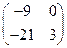 ;
; ;
; ;
;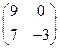 .
.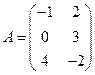 найдите матрицу АТ.
найдите матрицу АТ. ;
; ;
;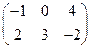 ;
; .
. .
. ;
; ;
; ;
; .
. и
и 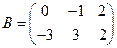 .
. ;
; ;
;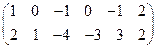 ;
; .
. найдите матрицу АТ.
найдите матрицу АТ.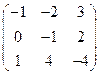 ;
; ;
;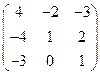 ;
; .
. на матрицу
на матрицу  .
.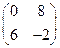 ;
;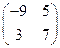 ;
;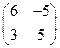 ;
; на число –2.
на число –2. ;
;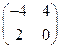 ;
;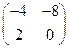 ;
; .
. и
и  .
. ;
;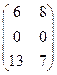 ;
; ;
; .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.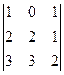 .
. .
. .
.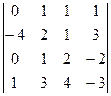 .
. .
. .
. .
. является множество всех векторов, сумма координат которых равна:
является множество всех векторов, сумма координат которых равна: и L
и L  векторного пространства V истинно равенство:
векторного пространства V истинно равенство: (m = 1)
(m = 1) 


