
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Метод координат на плоскостиСодержание книги Поиск на нашем сайте
(основные алгоритмы) 1. Косинус угла между векторами A)
2. Даны координаты вершин треугольника: А (-4;2), В (8;-6), С (2,6). Координаты точки пересечения медиан равны: A) (0;2); Б) (3;6); В) (1; 7); Г) (2;
3. Векторы A) 2; Б) -2; В)
4. Векторы A) -2; Б) 2; В)
5. Даны координаты точек А (3;5) и В (0;1). Расстояние между ними равно: А)2; Б)3; В)4; Г)5.
6. Длина вектора A)
7. Даны координаты вершин треугольника: А (2;-1), В (4;5); С (-3;2), Длина отрезка, соединяющего точку пересечения медиан треугольника АВС с началом координат, равна: A) 2; Б)
8. Даны координаты трех вершин параллелограмма ABCD: А (0; 2), В (3; 6); С (1; 7). Координаты четвертой вершины D равны: A) (2; -3); Б) (-2; 3); В) (3; 2); Г) (-3; -2).
9. Точка С делит отрезок АВ в отношении A) -3; Б) -2; В) 0; Г) -11.
10. Точка С делит отрезок АВ в отношении A) -3; Б) -2; В) 0; Г)
11. Векторы A)
12. Треугольник АВС построен на векторах A) 4; Б)
13. Даны точек А (4;7) и В (2;3). Если С – середина отрезка АВ, то произведение координат точки С равно: A) 15; Б) 10; В) 18; Г) -2.
14. Даны координаты точек А (0;0) и С (7;-5). Единичный вектор, сонаправленый с вектором А)
15. Даны координаты вершин треугольника: А (4;2), В (1;1), С (0;4). Угол при вершине В равен: A) 45°; Б) 90°; В) 135°; Г) 150°.
16. Векторы А) одинаково направлены; Б) противоположно направлены; В) перпендикулярны; Г) равны.
17. Угол между векторами А) острый; Б) прямой; В) не определен; Г) тупой.
18. Угол между векторами А) острый; Б) прямой; В) не определен; Г)тупой.
19. Угол между векторами А) прямой; Б) острый; В)тупой; Г) не определен.
20. Точка С делит отрезок АВ пополам и А (2;3), В (-1;-2), Сумма координат точки С равна: A) -3; Б) -2; В) 0; Г) 1.
21. Параллелограмм АВСD построен на векторах A) 14; Б) 19; В) 42; Г) 45.
22. Даны координаты вершин треугольника: А (2;-1), В (4;5), С (-3;2). Сумма координат точки пересечения медиан треугольника АВС равна: A) 2; Б)
23. Даны координаты точек А (3;5) и В (-3;3). Сумма координат середины отрезка равна: А)3; Б)4; В)5; Г)6.
24. Векторы A) α = -3; Б) α = 5; В) α =
25. Даны точки А (4;7) и С (2;3). Если С – середина отрезка АВ, то произведение координат точки В равно: A) 0; Б) 15; В) 18; Г) -2.
ТЕМА 2. ПРЯМАЯ НА ПЛОСКОСТИ (основные понятия и факты)
1. Прямая задана уравнением является вектор: А) (А; В) Б) (- А; В); В) (-В; А); Г) (А; - В).
2. Прямая задана уравнением является вектор: А) (А; В) Б) (- А; В); В) (-В; А); Г) (А; - В).
3. Если прямая имеет уравнение А) параллельна оси О х; Б) параллельна оси О y; В) проходит через начало координат; Г) параллельна биссектрисе первого и третьего координатных углов.
4. Если прямая имеет уравнение А) параллельна оси О х; Б) параллельна оси О y; В) проходит через начало координат; Г) параллельна биссектрисе первого и третьего координатных углов.
5. Если прямая имеет уравнение А) параллельна оси О х; Б) параллельна оси О y; В) проходит через начало координат; Г) параллельна биссектрисе первого и третьего координатных углов.
6. Прямые А) В)
7. Прямые А) В)
8. Прямые А) В)
9. Прямые А) В)
10. Прямые А) В)
11. Прямые А) В)
ТЕМА 2. ПРЯМАЯ НА ПЛОСКОСТИ (основные алгоритмы)
1. Прямая задана уравнением является вектор: А)
2. Общее уравнение прямой, проходящей через точку имеющей направляющий вектор
А) В)
3. Прямая задана уравнением является вектор: А)
4. Прямая
А) 300; Б) 450; В) 600; Г) 1350.
5. Уравнение прямой, отсекающей на осях координат отрезки
А) В) 6. Расстояние от точки
А) 20; Б) 0; В) 5; Г) 7. Диагонали ромба, равные 6 и 8 единицам, приняты за оси системы координат. Прямая, на которой лежит сторона ромба, расположенная в четвёртой четверти, задаётся уравнением:
А) В) 8. Прямая, проходящая через точку (1; 1) и параллельная прямой
А) В)
9. Каноническое уравнение биссектрисы второго и четвёртого координат- ных углов имеет вид:
А) В)
10. Общее уравнение прямой, проходящей через точку имеющей нормальный вектор
А) В) 11. Площадь треугольника, заключённого между координатными осями и прямой
А) 20; Б)
12. Параметрические уравнения прямой, проходящей через точки
А) В) 13. Прямая, проходящая через точку пересечения прямых
уравнение:
А) В)
14. Прямые
А) пересекаются; Б) параллельны, но различны; В) совпадают; Г) правильный ответ не указан.
15. Уравнение прямой, проходящей через точку с осью
А) В)
16. Четырёхугольник, стороны которого лежат на прямых
А) параллелограммом, но не прямоугольником; Б) трапецией; 4 В) прямоугольником, но не квадратом; Г) квадратом.
17. Точка из начала координат на прямую
А) В) 18. Величина угла между прямыми А)
19. Общее уравнение прямой
А) В)
20. Прямая
А) 21. Расстояние между параллельными прямыми равно:
А) 22. Величина угла между прямыми
А) 450; Б) В) 600; Г)
23. Угловой коэффициент прямой
А) 24. Расстояние между двумя параллельными прямыми
А) 10; Б) 25; В) 2; Г) 5. 25. Прямая задана параметрическими уравнениями: Нормальным к ней является вектор:
А)
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.43.109 (0.009 с.) |

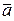 (1;5) и
(1;5) и 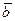 (5;3) равен:
(5;3) равен: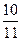 ; Б)
; Б) 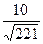 ; В)
; В) 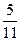 ; Г)
; Г)  .
.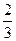 ).
). ; Г)
; Г) 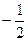 .
. равна 26, вектор
равна 26, вектор 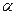 равно:
равно: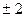 ; Б) 2; В)-2; Г)3.
; Б) 2; В)-2; Г)3. ; В)
; В)  ; Г)3.
; Г)3.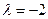 и А (2;3), В (-1;-2), Сумма координат точки С равна:
и А (2;3), В (-1;-2), Сумма координат точки С равна: и А (2;3), В (-1;-2), Сумма координат точки С равна:
и А (2;3), В (-1;-2), Сумма координат точки С равна: .
.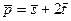 и
и 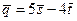 взаимно перпендикулярны. Угол между единичными векторами
взаимно перпендикулярны. Угол между единичными векторами 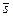 и
и 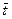 равен:
равен: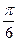 ; Б)
; Б) 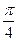 ; В)
; В)  ; Г)
; Г) 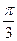 .
.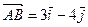 и
и  . Сторона АС равна:
. Сторона АС равна: ; В)
; В) 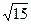 ; Г) 4,5.
; Г) 4,5. , имеет координаты:
, имеет координаты: ; Б)
; Б) 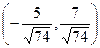 ; В)
; В) 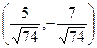 ; Г)
; Г)  .
. (2; 1) и
(2; 1) и 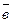 (-4; -2)
(-4; -2) (3; 4) и
(3; 4) и 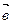 (3; -5)
(3; -5) (3; 4) и
(3; 4) и 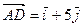 . Площадь параллелограмма равна:
. Площадь параллелограмма равна: и
и  перпендикулярны при следующем значении α:
перпендикулярны при следующем значении α: ; Г) α = -
; Г) α = -  . Направляющим для неё
. Направляющим для неё , то она
, то она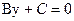 , то она
, то она , то она
, то она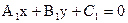 и
и 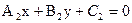 перпендикулярны, если:
перпендикулярны, если: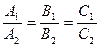 ; Б)
; Б) 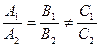 ;
;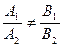 ; Г)
; Г) 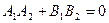 .
.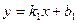 и
и 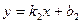 перпендикулярны, если:
перпендикулярны, если: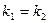 и
и 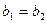 ; Б)
; Б) 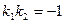 ;
;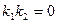 ; Г)
; Г) 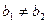 .
.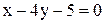 . Направляющим для неё
. Направляющим для неё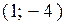 ; Б)
; Б) 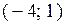 ; В)
; В) 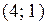 ; Г)
; Г) 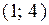 .
.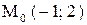 и
и =
= 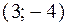 , принимает вид:
, принимает вид: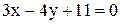 ; Б)
; Б)  ;
;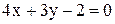 ; Г)
; Г)  .
. образует с осью
образует с осью 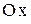 угол, равный:
угол, равный: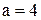 и
и , имеет вид:
, имеет вид: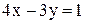 ; Б)
; Б) 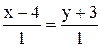 ;
; ; Г)
; Г) 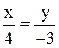 .
. до прямой
до прямой  равно:
равно: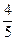 .
. ; Б)
; Б) 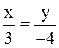 ;
;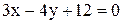 ; Г)
; Г)  .
. , имеет уравнение:
, имеет уравнение: ; Б)
; Б) 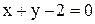 ;
;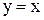 ; Г)
; Г) 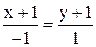 .
.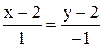 ; Б)
; Б)  ;
;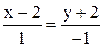 ; Г)
; Г) 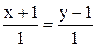 .
. =
= 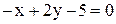 ; Б)
; Б)  .
.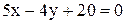 , равна:
, равна: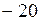 ; В) 10; Г)
; В) 10; Г)  .
. и
и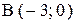 , имеют вид:
, имеют вид: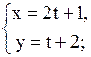 Б)
Б) 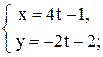
 Г)
Г) 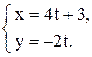
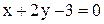 и
и и перпендикулярная прямой
и перпендикулярная прямой  и
и 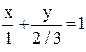 :
: и образующей
и образующей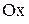 угол
угол 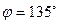 , имеет вид:
, имеет вид: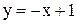 ; Б)
; Б) 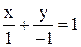 ;
;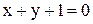 ; Г)
; Г) 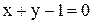 .
. ,
,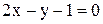 ,
, 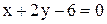 и
и  , является:
, является: . Прямая
. Прямая  ; Б)
; Б) 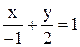 ;
;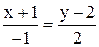 ; Г)
; Г) 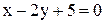 .
. и
и 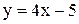 равна:
равна: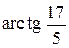 ; Б) 450; В)
; Б) 450; В) 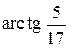 ; Г) 600.
; Г) 600. имеет вид: 3
имеет вид: 3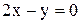 ; Б)
; Б) 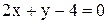 ;
;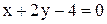 ; Г)
; Г) 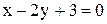 .
.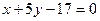 пересекает ось абсцисс в точке:
пересекает ось абсцисс в точке: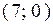 ; Б)
; Б)  ; В)
; В) 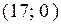 ; Г)
; Г) 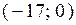 .
.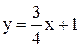 и
и 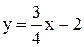
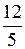 ; Б) 1; В) 3; Г)
; Б) 1; В) 3; Г) 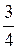 .
. и
и  равна:
равна: ;
;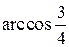 .
. равен:
равен: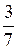 ; Б)
; Б) 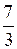 ; В)
; В)  ; Г)
; Г)  .
.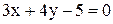 и
и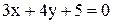 равно:
равно:
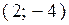 ; Б)
; Б)  ; В)
; В) 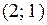 ; Г)
; Г) 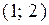 .
.


