
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системи лінійних рівнянь. Умови сумісності систем лінійних рівнянь.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Кронекера-Капеллі. Основні визначення Системою m лінійних рівнянь з n змінними x1, x2, …, xn називається система, яка має наступний вигляд: де аij – коефіцієнти при змінних; bi -вільні члени, Упорядкована сукупність чисел Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною. Система двох лінійних рівнянь з двома змінними має вигляд:
а систему трьох лінійних рівнянь з трьома змінними записують у вигляді: Система рівнянь називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля. Множина чисел аіа2,...,а п називається впорядкованою, якщо вказані порядок слідування цих чисел, яке з них є першим, яке другим, яке третім... Упорядкований набір п чисел називається розв'язком системи, якщо при підстановці цих чисел замість невідомих х1 х2, х п рівняння системи перетворюються у тотожні. Таку систему чисел називають також n-вимірним вектором, або точкою n-вимірного простору. Система рівнянь називається сумісною, якщо вона має хоч один розвязок, і несумісною, якщо вона не має жодного розв'язку. Сумісна система називається визначеною, якщо вона має один розв'язок. Сумісна система називається невизначеною, якщо вона має більше ніж один розв”язок. Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну множину розв'язків. Еквівалентні системи дістають внаслідок елементарних перетворень даної системи. Елементарні перетворення системи лінійних рівнянь відповідають елементарним перетворенням матриці, за умови, якщо вони виконуються над рядкам матриці.
Критерій сумісності системи лінійних рівнянь Нехай задано систему m лінійних рівнянь з п невідомими: апхх+апх2 +...+аихп =&,; a2lXl+a22x2 +...+аихп =Ь21;
Вичерпнішу відповідь про розв'язання дає теорема Кронекера Капелі. Теорема. Для того щоб система лінійних рівнянь була сумісною необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної матриці.
Якщо ранг основної матриці дорівнює рангу розширеної матриці і дорівнює числу невідомих, то система має єдиний розв 'язок. Якщо ранг основної матриці дорівнює рангу розширеної матриці то система має безліч розв 'язків. Приклад Дослідити на сумісність систему рівнянь
Оскільки ранг основної матриці г(А)=2, а ранг розширеної матриці г(А')=3, то задана система несумісна. Формули Крамера. Це правило можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають. Для простоти викладу розглянемо систему трьох лінійних рівнянь з трьома невідомими (
Позначимо визначники:
Визначник Якщо
і такий спосіб визначення невідомих називають правилом Крамера. Якщо Якщо
Приклад. Розв’язати систему лінійних рівнянь методом Крамера:
Розв’язання. Складемо і обчислимо визначники:
Підставимо одержані результати у формули (6). Маємо
Відповідь:
Метод Гауса. Для розв’язування систем лінійних рівнянь застосовують метод, який називають методом Гаусса або методом виключення змінних. Суть методу Гаусса розв’язування систем лінійних рівнянь розглянемо за допомогою матриць. Його ідея полягає у зведенні розширеної матриці системи за допомогою елементарних перетворень матриці до трикутної матриці.
Трикутною називають матрицю, у якої під головною діагоналлю всі елементи рівні нулю.
Елементарними перетвореннями матриці є такі перетворення: 1) перестановка двох рядків матриці; 2) множення всіх елементів рядка на одне і те ж число, відмінне від нуля; 3) додавання елементів якого-небудь рядка матриці, помножених на одне і те ж число, до відповідних елементів іншого рядка; 4) відкидання рядків матриці, елементами яких є нулі.
Проводячи елементарні перетворення над матрицею системи, отримують нову систему рівнянь, яка еквівалентна заданій, але з новими коефіцієнтами та вільними членами. Одержують трикутну систему рівнянь, із якої визначають невідомі.
Приклад. Методом Гаусса розв’язати систему лінійних рівнянь
Розв’язання. Складемо розширену матрицю системи і будемо робити над нею необхідні елементарні перетворення, щоб одержати трикутну матрицю. На початку переставимо перше і третє рівняння місцями, а потім помножимо елементи першого рядка відповідно на мінус три, мінус два та мінус два і одержані результати додамо відповідно до елементів другого, третього та четвертого рядків. Аналогічно вчинимо з елементами другого, а потім третього рядків. Одержимо матрицю
~ Система лінійних рівнянь матиме вигляд
З третього рівняння Відповідь:
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.247.108 (0.009 с.) |



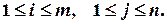
 , називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.
, називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей. (2.1)
(2.1)
 Складемо основну матрицю А і розширену матрицю А' даної системи:
Складемо основну матрицю А і розширену матрицю А' даної системи:
 ):
):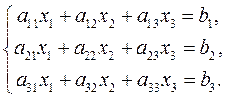 (5)
(5)

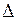 називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках
називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках 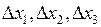 коефіцієнти при відповідних невідомих замінені вільними членами.
коефіцієнти при відповідних невідомих замінені вільними членами. , то система (5) має єдиний розв’язок. Невідомі визначають за формулами
, то система (5) має єдиний розв’язок. Невідомі визначають за формулами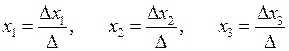 (6)
(6)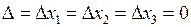 , то система (5) має безліч розв’язків, а правило Крамера застосувати не можна.
, то система (5) має безліч розв’язків, а правило Крамера застосувати не можна. , а хоча б один із визначників
, а хоча б один із визначників 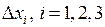 , відмінний від нуля, то система (5) несумісна.
, відмінний від нуля, то система (5) несумісна.




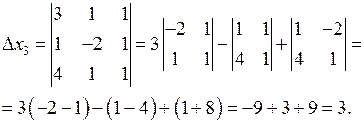

 .
.
 ~
~ 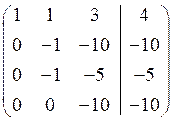 ~
~ 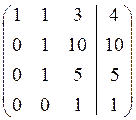 ~
~ ~
~  ~
~  ~
~  .
.
 . З другого рівняння одержали
. З другого рівняння одержали  , а з першого одержуємо
, а з першого одержуємо 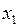 .
. .
.


