
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод виділення лінійних множниківСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод використовується, коли елементи визначника можна вважати многочленами від одної або кількох змінних. В цьому випадку і самий визначник є многочленом від цих змінних.
В основі метода знаходяться наступні відомі властивості многочленів 1) многочлен від деякої змінної степеня k має не більше ніж k коренів. 2) якщо f (x) – многочлен степеня k і x =a- корінь цього многочлена, то з многочлена виноситься множник (x- 3) якщо x =a1 і x =a2 – корені многочлена f (x) степеня k, a1 ¹ a2 і, згідно з попередньою властивістю, f (x) = (x -a1) g (x), де g (x) – многочлен степеня k -1, то x =a2, є коренем многочлена g (x), а тому многочлен f (x) можна подати у вигляді f (x) = (x -a1) (x -a2) h (x), де h (x) – многочлен степеня k -2. 4) з попередньої властивості випливає, що якщо f (x) – многочлен степеня k, a1, a2,..., a k – його різні корені, то f (x) = a (x -a1) (x -a2)… (x -a k), де a – старший коефіцієнт многочлена f (x).
Властивості визначників 1. Якщо всі елементи деякого рядка визначника дорівнюють нулю (нульовий рядок), то визначник дорівнює нулю. 2. Якщо у визначнику переставляються місцями два рядки, то змінюється лише знак визначника. Припустимо, що у визначнику D міняються місцями і -й і j -й рядки (і ¹ j), тоді D = 3. Якщо два рядки визначника співпадають, то визначник дорівнює нулю. 4. Якщо деякий рядок визначника помножується на число l, то визначник помножується на l. Припустимо, що у визначнику D = помножується на l і -й рядок, тоді
З цієї властивості випливає, що якщо всі елементи деякого рядка визначника помножені на деяке число l, то це число можна винести за знак визначника як множник.
Два рядки визначника називаються пропорційними, якщо один з них можна одержати помноженням другого на деяке число. 5. Якщо два рядки визначника пропорційні, то визначник дорівнює нулю. Нехай (bi 1, bi 2,…, bin) і (сi 1, сi 2,…, сin) – два рядки. Під сумою цих рядків розуміється рядок вигляду (bi 1+ сi 1, bi 2 + сi 2,…, bin + сin). 6. Якщо у визначнику D і-рядок є сумою двох рядків, то визначник D можна розкласти в суму двох визначників D1 і D2 за і-м рядком таким чином, що і-рядком визначника D1 є перший доданок, а і-м рядком визначника D2 – другий доданок і-го рядка визначника D. Решта рядків визначників D1 і D2 співпадають з відповідними рядками визначника D. Припустимо, що у визначнику D і -й рядок є сумою двох рядків, тоді D = Аналогічно, якщо і -й рядок визначника D є сумою k рядків, то визначник D можна розкласти в суму k визначників за і -м рядком. 7. Якщо до рядка визначника додати інший рядок, помножений на число, то визначник не змінюється. Нехай 8. Якщо у визначнику деякий рядок є лінійною комбінацією інших рядків, то визначник дорівнює нулю. 9. Якщо до рядка визначника додати лінійну комбінацію інших рядків, то визначник не змінюється. Обернена матриця. Ранг матриці Обернена матриця — для кожної невиродженої квадратної матриці
де Якщо для матриці Знаходження оберненої матриці
Властивості
Ранг мáтриці (математичний) — щонайвищий з порядків відмінних від нуля мінору цієї матриці. Ранг матриці рівний найбільшому числу лінійно-незалежних рядків (або стовпців) матриці. Причому ранг по стовпцям збігається з рангом по рядкам. Ранг матриці не міняється при елементарних перетвореннях матриці (перестановці рядків або стовпців, множенні рядка або стовпця на відмінне від нуля число і при складанні рядків або стовпців). Система лінійних рівнянь має розв'язок тоді і тільки тоді, коли ранг матриці, складеної з коефіцієнтів при невідомих, не змінюється при додаванні до неї стовпця вільних членів. Цей розв'язок єдиний, якщо цей ранг матриці дорівнює кількості невідомих. Ранг 5.Система лінійних алгебраїчних рівнянь.Їх сумісність. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:
Це система m лінійних рівнянь з n невідомими, де
Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії. Розв’язком системи лінійних алгебраїчних рівнянь є будь-яка сукупність дійсних чисел x 1, x 2,..., xn, яка при підстановці кожне рівняння системи перетворює його в тотожність. Якщо система має хоча б один розв’язок, то вона називається сумісною, і несумісною, якщо не має жодного. Відповідь на питання сумісності системи дає теорема Кронекера-Капеллі. Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має безліч розв’язків. В останньому випадку кожен її розв’язок називають частковим розв’язком системи. Сукупність усіх часткових розв’язків називають загальним розв’язком системи.
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ), тобто многочлен подається у вигляді f (x) = (x -a) g (x), де g (x) – многочлен степеня k -1.
), тобто многочлен подається у вигляді f (x) = (x -a) g (x), де g (x) – многочлен степеня k -1. = -
= -  .
.
 = l
= l  =
= 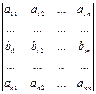 +
+  .
. ,
, 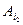 ,...,
,..., 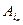 ‑ деякі рядки визначника D, а l 1, l 2,..., ln – деякі числа. Тоді рядок l 1
‑ деякі рядки визначника D, а l 1, l 2,..., ln – деякі числа. Тоді рядок l 1  , розмірності
, розмірності  , завжди існує обернена матриця, позначається
, завжди існує обернена матриця, позначається  така що:
така що:
 одинична
одинична  , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою.
, то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою. , тобто
, тобто 
 - союзна матриця.
- союзна матриця.
 — обернення транспонованої матриці
— обернення транспонованої матриці — обернення спряженої матриці
— обернення спряженої матриці для довільного коефіцієнта
для довільного коефіцієнта 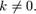

 — визначник оберненої матриці.
— визначник оберненої матриці. матриці розмірності
матриці розмірності  називають повним, якщо
називають повним, якщо  .
.
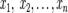 є невідомими,
є невідомими, є коефіцієнтами системи,
є коефіцієнтами системи, - вільними членами[1].
- вільними членами[1].


