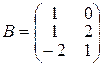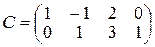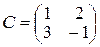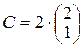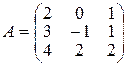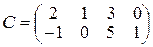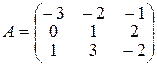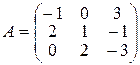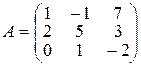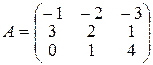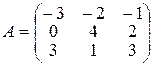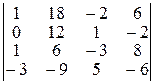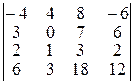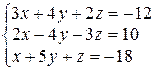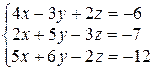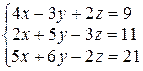Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системи лінійних алгебраїчних рівняньСодержание книги Поиск на нашем сайте
За допомогою систем лінійних алгебраїчних рівнянь моделюється переважна більшість практичних задач з економіки.
де Розв’язком системи лінійних алгебраїчних рівнянь називають таку сукупність чисел, яка перетворює всі рівняння (1.14) на числові тотожності. Якщо права частина (1.14) дорівнює нулю Система рівнянь (1.14) називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо не має жодного розв’язку. Складемо визначник третього порядку з коефіцієнтів систем – головний визначник системи:
Можливі наступні випадки розв’язку системи лінійних алгебраїчних рівнянь: 1) 2) Розв’язування системи лінійних алгебраїчних рівнянь за формулами Крамера: необхідно скласти три визначники третього порядку з головного визначника (1.15) шляхом перестановки замість 1, 2, 3–го стовпця стовпець вільних членів – це додаткові визначники
За формулами Крамера розв’язок системи рівнянь (1.14) має такий вигляд:
Метод Гаусса розв’язування системи лінійних алгебраїчних рівнянь: метод послідовних вилучень невідомих, запропонований Гауссом можна розглянути на прикладі системи (1.14), поділивши перше рівняння на
де
де Поділивши перше рівняння на
Віднявши перше рівняння від другого, дістанемо
звідки
Тепер можна знайти Матричний метод розв’язування системи лінійних алгебраїчних рівнянь: якщо систему (1.14) записати в матричній формі
де
Помножимо (1.23) на обернену матрицю
Розглянемо однорідну систему рівнянь:
Складемо головний визначник системи. При розв’язанні системи (1.26) можуть бути випадки:
1) 2)
Нехай із трьох визначників другого порядку цієї системи хоча б один не дорівнює нулеві, наприклад, визначник із коефіцієнтів при невідомих
Тоді система (1.27) є невизначеною і має безліч розв’язків, які знаходять за формулами:
де Може бути випадок, коли усі три визначники системи (1.27) дорівнюють нулю. Тоді одне з рівнянь системи є наслідком іншого і може бути відкинуто. Залишається одне рівняння системи (1.27), наприклад, перше. Якщо, наприклад,
де Індивідуальне завдання за темою „Лінійна алгебра” Завдання І. Задані матриці 1. Знайти величину визначника матриці а) використавши правило трикутника (правило Саррюса); б) розклавши визначник за елементами того рядка, який містить нуль; в) одержавши два нулі в будь-якому рядку і розклавши визначник по елементах цього рядка. 2. Знайти матрицю 3. Знайти два можливі добутки, утворені з матриць 4. Знайти матрицю
Завдання ІІ. Знайти величину визначника четвертого порядку, скориставшись його властивостями та одержавши три нулі в будь-якому рядку.
Завдання ІІІ. Розв’язати систему лінійних алгебраїчних рівнянь трьома способами: а) за формулами Крамера; б) методом Гаусса; в) методом оберненої матриці.
Розділ 2. Векторна алгебра
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.163.43 (0.009 с.) |

 ,
,
 – коефіцієнти рівняння;
– коефіцієнти рівняння;  – невідомі рівняння;
– невідомі рівняння;  – вільні члени рівняння.
– вільні члени рівняння.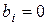 , то систему рівнянь називають однорідною, або неоднорідною, якщо
, то систему рівнянь називають однорідною, або неоднорідною, якщо  .
. .
.
 , тоді система (1.14) має єдиний розв’язок, який можна знайти або за формулами Крамера, або методом Гаусса, або матричним способом;
, тоді система (1.14) має єдиний розв’язок, який можна знайти або за формулами Крамера, або методом Гаусса, або матричним способом; , тоді система (1.14) або несумісна, або має безліч розв’язків.
, тоді система (1.14) або несумісна, або має безліч розв’язків. .
.
 .
.
 , друге – на
, друге – на  , третє – на
, третє – на  , матимемо:
, матимемо: ,
,
 . Віднявши від другого і третього рівняння перше, дістанемо
. Віднявши від другого і третього рівняння перше, дістанемо ,
,
 .
. , а друге – на
, а друге – на  , отримаємо
, отримаємо .
.
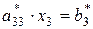 ,
,
 .
.
 та
та  .
. .
.
 – матриця коефіцієнтів системи;
– матриця коефіцієнтів системи; – матриця невідомих;
– матриця невідомих; – матриця вільних членів.
– матриця вільних членів. .
.
 . Оскільки
. Оскільки  , то дістанемо матричний спосіб розв’язування систем:
, то дістанемо матричний спосіб розв’язування систем: .
.
 .
.
 ;
; .
.
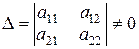 .
.
 .
.
 ,
,  ,
,  – довільне дійсне число.
– довільне дійсне число. ,
,
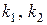 – довільні дійсні числа.
– довільні дійсні числа. . Необхідно:
. Необхідно: ) трьома способами:
) трьома способами: , де
, де  – одинична матриця третього порядку.
– одинична матриця третього порядку.