
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектори у декартовій системі координатСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
У прямокутній декартовій системі координат розглянемо довільний вектор Вектор Вектори
Вектор
Кожний з цих складових векторів можна надати у вигляді:
де Точка Довільний вектор
Подання вектора у вигляді суми компонентів (2.5) називається розкладанням вектора за координатним базисом (рис. 2.7). Довжина (модуль) вектора визначається за формулою
На рисунку 2.7 вектор
Лінійні операції над векторами у координатній формі: Дано вектори 1) додавання та віднімання
2) множення вектора на скаляр
Умови колінеарності двох векторів
Скалярний добуток векторів Скалярним добутком двох векторів
Фізичне тлумачення скалярного добутку двох векторів полягає в тому, що такий добуток являє собою роботу, виконану при переміщенні матеріальної точки під дією одного вектора вздовж другого. Беручи до уваги властивості проекції вектора на вісь, маємо (рис. 2.9)
Властивості скалярного добутку векторів: 1) 2)
3) 4) 5) 6) добутки ортів Якщо вектори задані в координатній формі
Основні задачі, які розв’язуються з використанням скалярного добутку векторів: 1) довжина вектора
2) косинус кута між векторами
3) проекція вектора на інший вектор
4) умова перпендикулярності
Векторний добуток векторів Векторним добутком векторів – напрям вектора – вектор – довжина вектора
Геометричний зміст векторного добутку: модуль векторного добутку векторів дорівнює площі паралелограма, сторонами якого є дані вектори. Властивості векторного добутку векторів: 1) 2) 3) 4) 5) 6) добутки ортів Якщо вектори задані в координатній формі
Основні задачі, які розв’язуються з використанням векторного добутку векторів: 1) площа паралелограма, побудованого на векторах
2) площа трикутника, побудованого на векторах
3) висота паралелограма
4) висота трикутника
Змішаний добуток векторів Змішаним (або векторно-скалярним) добутком трьох векторів
Змішаний добуток трьох векторів – це скалярний добуток одного з цих векторів на векторний добуток двох інших векторів. Геометричний зміст змішаного добутку: модуль змішаного добутку трьох векторів дорівнює об’єму паралелепіпеда (рис. 2.11), побудованого на цих векторах, як на його ребрах.
Якщо вектори задані в координатній формі
Властивості змішаного добутку векторів: 1) 2) 3) 4) 5)
6) Основні задачі, які розв’язуються з використанням змішаного добутку векторів: 1) об’єм паралелепіпеда, побудованого на векторах
2) об’єм піраміди, побудованої на векторах
3) висота паралелепіпеда
4) висота піраміди
Індивідуальне завдання за темою „Векторна алгебра” Дано координати точок 1. Знайти модуль та напрямок вектора 2. Знайти кут між векторами 3. Знайти проекцію вектора 4. Знайти вектор 5. Обчислити площу трикутника АВС. 6. Знайти висоту паралелограма, побудованого на векторах 7. Обчислити об’єм піраміди 8. Перевірити, чи колінеарні вектори 9. Перевірити, чи ортогональні вектори 10. Перевірити, чи належать точки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.232.244 (0.013 с.) |

 (рис..6).
(рис..6). називають полярним радіусом-вектором точки М. Спроектуємо цей вектор на координатні осі. Інакше кажучи, розкладемо вектор
називають полярним радіусом-вектором точки М. Спроектуємо цей вектор на координатні осі. Інакше кажучи, розкладемо вектор 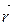 на складові вектори за координатними осями. Як показано на рис. 2.6 точки
на складові вектори за координатними осями. Як показано на рис. 2.6 точки 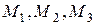 – проекції точки
– проекції точки  на відповідні координатні осі.
на відповідні координатні осі. – складові вектора
– складові вектора  за відповідними координатними осями.
за відповідними координатними осями.
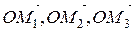 , тобто
, тобто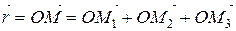 .
.
 ,
,  ,
, 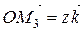 , де
, де 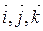 – базисні вектори декартової системи координат у просторі. Підставляючи ці значення в (2.3), одержуємо:
– базисні вектори декартової системи координат у просторі. Підставляючи ці значення в (2.3), одержуємо: ,
,
 – скалярні величини, які називаються координатами радіус-вектора
– скалярні величини, які називаються координатами радіус-вектора 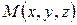 . Координати точки у просторі або її радіус-вектор
. Координати точки у просторі або її радіус-вектор  можна надати у вигляді:
можна надати у вигляді: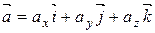 .
.
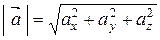 .
.

 утворює з координатними осями
утворює з координатними осями  кути
кути 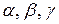 відповідно. Тоді
відповідно. Тоді  називаються напрямними косинусами вектора
називаються напрямними косинусами вектора 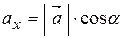 ,
, 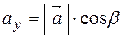 ,
,  ;
;

 та
та  :
: ;
;
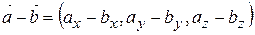 ;
;
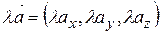 .
.
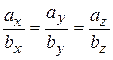 .
.
 (рис. 2.8) називається скаляр, який дорівнює добутку модулів цих векторів на косинус кута між ними:
(рис. 2.8) називається скаляр, який дорівнює добутку модулів цих векторів на косинус кута між ними: .
.

 .
.
 ;
; ;
; ;
; ;
; , якщо
, якщо  ;
; ,
, 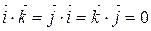 .
.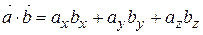 .
.
 ;
;
 ;
;
 ;
;
 .
.
 , який задовольняє умови:
, який задовольняє умови: такий, що він перпендикулярний до площини, в якій лежать вектори
такий, що він перпендикулярний до площини, в якій лежать вектори  ;
; .
.

 ;
;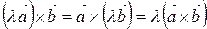 ;
; ;
; ;
; , якщо
, якщо  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.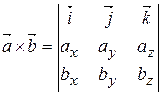 .
.
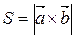 ;
;
 ;
;
 ;
;
 .
.
 .
.

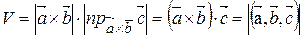
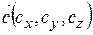 , то змішаний добуток векторів можна записати у вигляді
, то змішаний добуток векторів можна записати у вигляді .
.
 ;
; ;
; ;
; , якщо вектори
, якщо вектори 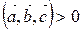 , якщо вектори
, якщо вектори  , якщо вектори
, якщо вектори  ;
;
 ;
;
 ;
;
 .
.
 . Необхідно:
. Необхідно: у просторі.
у просторі. та
та 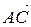 .
. на напрям вектора
на напрям вектора  .
. і до
і до  .
. .
.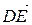 .
.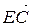 .
. до однієї площини.
до однієї площини. (0; -1; 2)
(0; -1; 2)
 (1; 2; 1)
(1; 2; 1)
 (-3; 2; 1)
(-3; 2; 1)
 (0; 0; -1)
(0; 0; -1)
 (2; 6; -3)
(2; 6; -3)



