

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Криві другого порядку: коло, еліпс, гіпербола та парабола
Коло – це геометричне місце точок площини, рівновіддалених від даної точки  , яку називають центром кола; , яку називають центром кола;  – радіус кола. – радіус кола.
Рівняння кола має вид (3.12). Якщо центр кола співпадає з початком координат, то рівняння кола має вид (3.13)

| 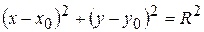 ; ;
| (3.12)
|  . .
| (3.13)
| | Рис. 3.5
|
| Еліпсом називається геометричне місце точок площини, сума відстаней яких від двох заданих точок  та та  , що називаються фокусами, є величина стала , що називаються фокусами, є величина стала  , причому ця величина більша за відстань між фокусами. , причому ця величина більша за відстань між фокусами.

|  та та  – фокуси еліпса; – фокуси еліпса;
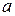 – велика піввісь; – велика піввісь;
 – мала піввісь; – мала піввісь;
 – фокусна відстань; – фокусна відстань;
 – ексцентриситет; – ексцентриситет;
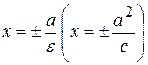 – рівняння директрис. – рівняння директрис.
| | Рис. 3.6
|
| Канонічне рівняння еліпса з фокусами на осі  має вид має вид
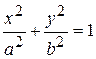 . .
| (3.14)
| Основна властивість еліпса полягає у співвідношенні
 . .
| (3.15)
| Форма еліпса характеризується ексцентриситетом. Значення ексцентриситету  оцінює «сплющеність» еліпса. оцінює «сплющеність» еліпса.
 . .
| (3.16)
| Якщо  , то при , то при  маємо коло, при маємо коло, при 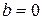 , , 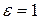 – відрізок. Це випадки виродженого еліпса. – відрізок. Це випадки виродженого еліпса.
Відстань деякої точки еліпса 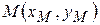 до його фокусів називаються фокальними радіусами: до його фокусів називаються фокальними радіусами:
 – правий, – правий,
 – лівий, – лівий,
| (3.17)
|  . .
| (3.18)
| Гіперболою називається геометричне місце точок, різниця відстаней яких від двох заданих точок  та та  , що називаються фокусами, є величина стала , що називаються фокусами, є величина стала  , причому ця величина менша за відстань між фокусами. , причому ця величина менша за відстань між фокусами.

|  та та  – фокуси гіперболи; – фокуси гіперболи;
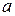 – дійсна піввісь; – дійсна піввісь;
 – уявна піввісь; – уявна піввісь;
 – фокусна відстань; – фокусна відстань;
 – ексцентриситет; – ексцентриситет;
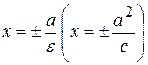 – рівняння директрис; – рівняння директрис;
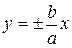 – рівняння асимптот. – рівняння асимптот.
| | Рис. 3.7
|
| Канонічне рівняння гіперболи з фокусами на осі  має вид має вид
 . .
| (3.19)
| Основна властивість гіперболи полягає у співвідношенні
 . .
| (3.20)
| Значення ексцентриситету  гіперболи гіперболи
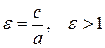 . .
| (3.21)
| Відстань деякої точки гіперболи 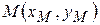 до його фокусів називаються фокальними радіусами: до його фокусів називаються фокальними радіусами:
 – правий, – правий,
 – лівий, – лівий,
| (3.22)
|  . .
| (3.23)
| Параболою називається геометричне місце точок площини, рівновіддалених від заданої точки  , яка називається фокусом, і від заданої прямої , яка називається фокусом, і від заданої прямої  , яка називається директрисою. , яка називається директрисою.

|
 – фокус параболи; – фокус параболи;
 – рівняння директриси. – рівняння директриси.
| | Рис. 3.8
|
| Канонічне рівняння параболи, симетричної відносно осі  має вид має вид
 . .
| (3.24)
| Якщо  , то вітки параболи розташовані праворуч, а якщо , то вітки параболи розташовані праворуч, а якщо  – ліворуч. – ліворуч.
Парабола  симетрична відносно осі симетрична відносно осі  : якщо : якщо  , то вітки даної параболи розташовані догори, а якщо , то вітки даної параболи розташовані догори, а якщо  – донизу. – донизу.
Індивідуальне завдання за темою „Аналітична геометрія на площині”
Завдання І. Задані координати вершин трикутника АВС. Знайти:
1) рівняння сторони АВ, записати його у вигляді рівняння у відрізках;
2) рівняння прямої BK, що проходить через точку В паралельно стороні АС;
3) рівняння висоти СD та її довжини;
4) кут між висотою CD та медіаною ВМ;
5) побудувати усі лінії.
| Варіант 1
| A (6;2)
| B (30;-5)
| C (12;19)
| | Варіант 2
| A (4;3)
| B (-12;-9)
| C (-5;15)
| | Варіант 3
| A (-1;7)
| B (11;2)
| C (17;10)
| | Варіант 4
| A (1;1)
| B (-15;11)
| C (-8;13)
| | Варіант 5
| A (-14;10)
| B (10;3)
| C (-8;27)
| | Варіант 6
| A (7;1)
| B (-5;-4)
| C (-9;-1)
| | Варіант 7
| A (-2;1)
| B (-18;-11)
| C (-11;13)
| | Варіант 8
| A (10;-1)
| B (-2;-6)
| C (-6;-3)
| | Варіант 9
| A (-12;6)
| B (12;-1)
| C (-6;23)
| | Варіант 10
| A (8;0)
| B (-4;-5)
| C (-8;-2)
| | Варіант 11
| A (11;0)
| B (-5;4)
| C (-1;-1)
| | Варіант 12
| A (10;2)
| B (-6;6)
| C (-2;1)
| | Варіант 13
| A (14;0)
| B (-2;4)
| C (2;-1)
| | Варіант 14
| A (13;2)
| B (-3;6)
| C (1;1)
| | Варіант 15
| A (11;3)
| B (-5;7)
| C (-1;2)
| | Варіант 16
| A (13;-1)
| B (-3;3)
| C (1;-2)
| | Варіант 17
| A (11;-2)
| B (-5;6)
| C (-1;1)
| | Варіант 18
| A (13;0)
| B (-3;4)
| C (1;-1)
| | Варіант 19
| A (11;-1)
| B (-5;3)
| C (-1;-2)
| | Варіант 20
| A (13;3)
| B (-3;7)
| C (1;2)
| | Варіант 21
| A (6;2)
| B (30;-5)
| C (12;19)
| | Варіант 22
| A (4;3)
| B (-12;-9)
| C (-5;15)
| | Варіант 23
| A (-1;7)
| B (11;2)
| C (17;10)
| | Варіант 24
| A (1;1)
| B (-15;11)
| C (-8;13)
| | Варіант 25
| A (-14;10)
| B (10;3)
| C (-8;27)
| | Варіант 26
| A (7;1)
| B (-5;-4)
| C (-9;-1)
| | Варіант 27
| A (-2;1)
| B (-18;-11)
| C (-6;-3)
| | Варіант 28
| A (10;-1)
| B (-2;-6)
| C (-6;23)
| | Варіант 29
| A (-12;6)
| B (12;-1)
| C (-6;23)
| | Варіант 30
| A (8;0)
| B (-4;-5)
| C (-8;-2)
| Завдання ІІ. Звести до канонічного вигляду рівняння кривої другого порядку, визначити її вид та знайти всі її параметри. Побудувати криву другого порядку.
| Варіант 1
| 
| | Варіант 2
| 
| | Варіант 3
| 
| | Варіант 4
| 
| | Варіант 5
| 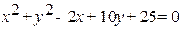
| | Варіант 6
| 
| | Варіант 7
| 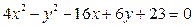
| | Варіант 8
| 
| | Варіант 9
| 
| | Варіант 10
| 
| | Варіант 11
| 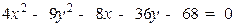
| | Варіант 12
| 
| | Варіант 13
| 
| | Варіант 14
| 
| | Варіант 15
| 
| | Варіант 16
| 
| | Варіант 17
| 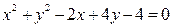
| | Варіант 18
| 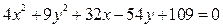
| | Варіант 19
| 
| | Варіант 20
| 
| | Варіант 21
| 
| | Варіант 22
| 
| | Варіант 23
| 
| | Варіант 24
| 
| | Варіант 25
| 
| | Варіант 26
| 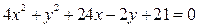
| | Варіант 27
| 
| | Варіант 28
| 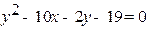
| | Варіант 29
| 
| | Варіант 30
| 
|
Завдання ІІІ
| Варіант 1
| Скласти канонічне рівняння еліпса, якщо відомо, що еліпс проходить через точку А(0;-3) та його ексцентриситет дорівнює 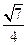 . .
| | Варіант 2
| На параболі  знайти точку, відстань якої від директриси дорівнює 10. знайти точку, відстань якої від директриси дорівнює 10.
| | Варіант 3
| Скласти рівняння кола, що проходить через лівий фокус еліпса  і має центр у точці А(-1;-3). і має центр у точці А(-1;-3).
|
| Варіант 4
| Скласти канонічне рівняння гіперболи, якщо відомо, що точки А( ;0) та В( ;0) та В( ;1) лежать на гіперболі. ;1) лежать на гіперболі.
| | Варіант 5
| Скласти канонічне рівняння еліпса, якщо його фокуси F1(0; 0), F2(1; 1), а його велика вісь дорівнює 2.
| | Варіант 6
| Скласти канонічне рівняння параболи, якщо відомо, що парабола симетрична відносно осі ординат ОY та проходить через точки O(0;0) і N(6;-2).
| | Варіант 7
| Скласти рівняння кола, що проходить через точку О(0;0) і має центр в точці А, де А – вершина параболи  . .
| | Варіант 8
| Скласти канонічне рівняння гіперболи, якщо відомо, що відстань між вершинами дорівнює 8, а відстань між фокусами дорівнює 10.
| | Варіант 9
| Скласти канонічне рівняння еліпса, якщо відомо, що його мала вісь дорівнює 24, а відстань між фокусами дорівнює 10.
| | Варіант 10
| Скласти канонічне рівняння параболи, якщо відомо, що парабола симетрична відносно осі абсцис та проходить через точки O(0;0) і М(1;-4).
| | Варіант 11
| Скласти рівняння кола, що проходить через лівий фокус гіперболи  і має центр у точці А(0;-3). і має центр у точці А(0;-3).
| | Варіант 12
| Скласти канонічне рівняння гіперболи, якщо відомо, що дійсна вісь гіперболи дорівнює 5, а вершини ділять відстань між центром і фокусом навпіл.
| | Варіант 13
| Скласти канонічне рівняння еліпса, що проходить через дві точки А(3;0) та В(2;  ). ).
| | Варіант 14
| Скласти канонічне рівняння параболи, якщо відомо, що парабола має фокус Р(0;2) та вершину в точці О(0;0).
| | Варіант 15
| Скласти рівняння кола, що проходить через фокуси гіперболи  і має центр у точці А(0;-8). і має центр у точці А(0;-8).
| | Варіант 16
| Скласти канонічне рівняння гіперболи, якщо відомо, що дійсна вісь дорівнює 6, і гіпербола проходить через точку А(9;-4).
| | Варіант 17
| Скласти канонічне рівняння еліпса, якщо відомо, що відстань між фокусами дорівнює 6, а ексцентриситет дорівнює  . .
| | Варіант 18
| Скласти рівняння параболи, якщо відоме рівняння директриси кривої  . .
| | Варіант 19
| Скласти рівняння кола, що проходить через фокуси еліпса 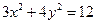 і має центр у точці А, де А – його верхня вершина. і має центр у точці А, де А – його верхня вершина.
| | Варіант 20
| Скласти канонічне рівняння гіперболи, якщо її ексцентриситет дорівнює 2, а фокуси співпадають з фокусами еліпса з рівнянням  . .
|
| Варіант 21
| Скласти канонічне рівняння еліпса, якщо відомо, що відстань між фокусами дорівнює 4, а відстань між директрисами дорівнює 5.
| | Варіант 22
| Скласти рівняння параболи, якщо відоме рівняння директриси кривої  . .
| | Варіант 23
| Скласти рівняння кола, що проходить через фокуси еліпса  і має центр у точці А(0;6). і має центр у точці А(0;6).
| | Варіант 24
| Скласти канонічне рівняння гіперболи, вершини та фокуси якої знаходяться у відповідних фокусах і вершинах еліпса  . .
| | Варіант 25
| Скласти канонічне рівняння еліпса, якщо відомо, що відстань між директрисами дорівнює 32, а ексцентриситет дорівнює 0,5.
| | Варіант 26
| Скласти канонічне рівняння параболи, якщо вона має вісь симетрії ОХ та проходить через точку А(-2;6).
| | Варіант 27
| Скласти рівняння кола, що проходить через правий фокус еліпса  і має центр у точці А(1;7). і має центр у точці А(1;7).
| | Варіант 28
| Скласти канонічне рівняння гіперболи, якщо відомі рівняння її асимптот 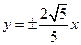 та фокусна відстань дорівнює та фокусна відстань дорівнює  . .
| | Варіант 29
| Скласти канонічне рівняння еліпса, що має вершини в фокусах, а фокуси у вершинах гіперболи  . .
| | Варіант 30
| Скласти рівняння кола, що проходить через вершини гіперболи  і має центр у точці А(0;4). і має центр у точці А(0;4).
|
|



 , яку називають центром кола;
, яку називають центром кола;  – радіус кола.
– радіус кола.
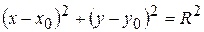 ;
;
 .
.
 та
та  , що називаються фокусами, є величина стала
, що називаються фокусами, є величина стала  , причому ця величина більша за відстань між фокусами.
, причому ця величина більша за відстань між фокусами.
 та
та  – фокуси еліпса;
– фокуси еліпса;
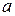 – велика піввісь;
– велика піввісь;
 – мала піввісь;
– мала піввісь;
 – фокусна відстань;
– фокусна відстань;
 – ексцентриситет;
– ексцентриситет;
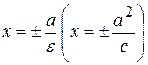 – рівняння директрис.
– рівняння директрис.
 має вид
має вид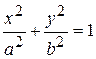 .
.
 .
.
 .
.
 , то при
, то при  маємо коло, при
маємо коло, при 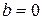 ,
, 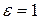 – відрізок. Це випадки виродженого еліпса.
– відрізок. Це випадки виродженого еліпса.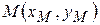 до його фокусів називаються фокальними радіусами:
до його фокусів називаються фокальними радіусами: – правий,
– правий,
 – лівий,
– лівий,
 .
.

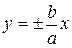 – рівняння асимптот.
– рівняння асимптот.
 .
.
 .
.
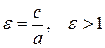 .
.
 – правий,
– правий,
 – лівий,
– лівий,
 .
.
 , яка називається фокусом, і від заданої прямої
, яка називається фокусом, і від заданої прямої  , яка називається директрисою.
, яка називається директрисою.
 – фокус параболи;
– фокус параболи;
 – рівняння директриси.
– рівняння директриси.
 .
.
 , то вітки параболи розташовані праворуч, а якщо
, то вітки параболи розташовані праворуч, а якщо  – ліворуч.
– ліворуч. симетрична відносно осі
симетрична відносно осі  : якщо
: якщо 



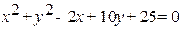

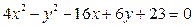



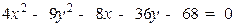





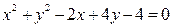
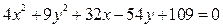







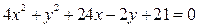

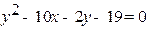


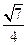 .
.
 знайти точку, відстань якої від директриси дорівнює 10.
знайти точку, відстань якої від директриси дорівнює 10.
 і має центр у точці А(-1;-3).
і має центр у точці А(-1;-3).
 ;0) та В(
;0) та В( ;1) лежать на гіперболі.
;1) лежать на гіперболі.
 .
.
 і має центр у точці А(0;-3).
і має центр у точці А(0;-3).
 ).
).
 і має центр у точці А(0;-8).
і має центр у точці А(0;-8).
 .
.
 .
.
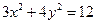 і має центр у точці А, де А – його верхня вершина.
і має центр у точці А, де А – його верхня вершина.
 .
.
 .
.
 .
.
 і має центр у точці А(1;7).
і має центр у точці А(1;7).
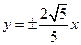 та фокусна відстань дорівнює
та фокусна відстань дорівнює  .
.
 .
.
 і має центр у точці А(0;4).
і має центр у точці А(0;4).



