
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення та основні властивості визначниківСодержание книги
Поиск на нашем сайте
Вступ Методичні вказівки та індивідуальні завдання з курсу вищої математики за темами „Лінійна та векторна алгебра” та „Аналітична геометрія на площині та у просторі” складено відповідно до програми курсу. Мета розробки: перевірка знань студентів з основних понять і методів курсу, прищеплення у студентів навичок самостійної роботи. Типові розрахунки можуть бути використані викладачами для контролю знань студентів, для проведення аудиторних індивідуальних практичних занять, а також як домашні індивідуальні завдання. Розділ 1. Лінійна алгебра Матриці та дії над ними Поняття матриці та відповідний розділ математики мають важливе значення для економістів, оскільки велика кількість досліджувальних об’єктів і процесів досить просто, а головне – компактно, подається в матричній формі. Матрицею розміру
де Матриці бувають різних типів: прямокутні, квадратні, діагональні, одиничні, нульові та інші. Квадратною матрицею називається матриця, в якій кількість рядків і стовпців однакова. Їх кількість вказує розмір матриці. Головною діагоналлю квадратної матриці називається діагональ, яка проходить через верхній лівий та нижній правий кути матриці, тобто сукупність елементів Квадратну матрицю, в якій всі елементи, окрім тих, що розташовані на головній діагоналі, дорівнюють нулю, називають діагональною матрицею. Діагональну матрицю, в якій всі елементи дорівнюють одиниці, називають одиничною і позначають літерою
Матриця називається трикутною, якщо всі її елементи під (над) діагоналлю дорівнюють нулю. Нульовою матрицею називається матриця, всі елементи якої дорівнюють нулю. Над матрицями, як і над числами, можна виконувати різні операції, причому деякі з них – аналогічні операціям над числами, а деякі – специфічні. Розрізняють наступні дії над матрицями: 1. Операція порівняння: дві матриці 2. Множення матриці на число: добутком матриці
3. Додавання та віднімання матриць: сумою двох матриць
Додавати можна матриці лише однакового розміру, тобто матриці з однаковою кількістю рядків і стовпців. Властивості операцій додавання та віднімання матриць: - - - - 4. Транспонування матриці: транспонованою матрицею до матриці 5. Множення матриць: добутком двох матриць
Перемножать можливо лише такі дві матриці, в яких кількість стовпців першої збігається з кількістю рядків другої:
Добутком двох матриць є матриця, в якій кількість рядків дорівнює кількості рядків першої матриці, а кількість стовпців – кількості стовпців другої матриці. Властивості добутку матриць: - - - - - - Розділ 2. Векторна алгебра Проекція вектор на вісь Нехай існує вектор Проекцією
Проекція
Оскільки Властивості проекції на вісь: - - - - проекція замкнутої векторної лінії на вісь дорівнює нулю. Скалярний добуток векторів Скалярним добутком двох векторів
Фізичне тлумачення скалярного добутку двох векторів полягає в тому, що такий добуток являє собою роботу, виконану при переміщенні матеріальної точки під дією одного вектора вздовж другого. Беручи до уваги властивості проекції вектора на вісь, маємо (рис. 2.9)
Властивості скалярного добутку векторів:
1) 2) 3) 4) 5) 6) добутки ортів Якщо вектори задані в координатній формі
Основні задачі, які розв’язуються з використанням скалярного добутку векторів: 1) довжина вектора
2) косинус кута між векторами
3) проекція вектора на інший вектор
4) умова перпендикулярності
Векторний добуток векторів Векторним добутком векторів – напрям вектора – вектор – довжина вектора
Геометричний зміст векторного добутку: модуль векторного добутку векторів дорівнює площі паралелограма, сторонами якого є дані вектори. Властивості векторного добутку векторів: 1) 2) 3) 4) 5) 6) добутки ортів Якщо вектори задані в координатній формі
Основні задачі, які розв’язуються з використанням векторного добутку векторів: 1) площа паралелограма, побудованого на векторах
2) площа трикутника, побудованого на векторах
3) висота паралелограма
4) висота трикутника
Змішаний добуток векторів Змішаним (або векторно-скалярним) добутком трьох векторів
Змішаний добуток трьох векторів – це скалярний добуток одного з цих векторів на векторний добуток двох інших векторів. Геометричний зміст змішаного добутку: модуль змішаного добутку трьох векторів дорівнює об’єму паралелепіпеда (рис. 2.11), побудованого на цих векторах, як на його ребрах.
Якщо вектори задані в координатній формі
Властивості змішаного добутку векторів: 1) 2) 3) 4) 5) 6) Основні задачі, які розв’язуються з використанням змішаного добутку векторів: 1) об’єм паралелепіпеда, побудованого на векторах
2) об’єм піраміди, побудованої на векторах
3) висота паралелепіпеда
4) висота піраміди
Індивідуальне завдання за темою „Векторна алгебра” Дано координати точок 1. Знайти модуль та напрямок вектора 2. Знайти кут між векторами 3. Знайти проекцію вектора 4. Знайти вектор 5. Обчислити площу трикутника АВС. 6. Знайти висоту паралелограма, побудованого на векторах 7. Обчислити об’єм піраміди 8. Перевірити, чи колінеарні вектори 9. Перевірити, чи ортогональні вектори 10. Перевірити, чи належать точки
Пряма лінія на площині
Рівняння Задавши на площини систему координат, можна положення будь-якої прямої визначати різними способами, тобто за допомогою різних параметрів. В залежності від вибору цих параметрів розрізняють наступні види рівнянь прямої: 1. Рівняння прямої, що проходить через задану точку
Орієнтацію прямої
2. Загальне рівняння прямої:
Дослідимо рівняння (3.2): – при – при – при – при – при 3. Канонічне рівняння прямої (3.3) та параметричне рівняння прямої (3.4):
Пряма лінія (рис. 3.2), що задана рівняннями виду (3.3) або (3.4), проходить через задану точку
4. Рівняння прямої, яка проходить через дві задані точки
5. Рівняння прямої у відрізках на осях
6. Рівняння прямої з кутовим коефіцієнтом (рис. 3.4)
де 7. Рівняння прямої, яка проходить у заданому напряму через задану точку (рівняння в’язки) (рис. 3.4):
8. Нормальне рівняння прямої (рис.3.4):
де 9. Відстань від точки – якщо пряма задана рівнянням виду (3.9)
– якщо пряма задана рівнянням виду (3.2)
Взаємне розташування двох прямих на площині:
Завдання ІІІ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.73.169 (0.013 с.) |

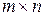 називається множина з
називається множина з 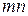 елементів
елементів  , розміщених у вигляді прямокутної таблиці з
, розміщених у вигляді прямокутної таблиці з  рядків і
рядків і 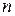 стовпців:
стовпців:
 ,
,
 – номер рядка;
– номер рядка; 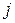 – номер стовпця.
– номер стовпця. .
. .
. .
.
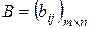 називаються рівними
називаються рівними  , якщо рівні їх відповідні елементи, тобто
, якщо рівні їх відповідні елементи, тобто  .
. на число
на число  називається матриця
називається матриця  , елементи якої визначаються за формулою
, елементи якої визначаються за формулою .
.
 називається матриця
називається матриця  .
.
 (комутативність);
(комутативність); (асоціативність);
(асоціативність);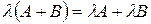 (дистрибутивність);
(дистрибутивність);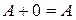 (нейтральність нульової матриці).
(нейтральність нульової матриці). .
.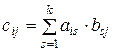 .
.
 .
.
 ;
;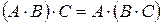 ;
; ;
;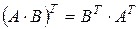 ;
; ;
; .
. та вісь
та вісь  (рис. 2.5). Вектор
(рис. 2.5). Вектор  ,
,  – кут між вектором
– кут між вектором  та
та  – проекції точок
– проекції точок  вектора
вектора  .
.
 на косинус кута між напрямком вектора
на косинус кута між напрямком вектора  .
.
 може бути в залежності від значення кута
може бути в залежності від значення кута 
 ;
; ;
; та
та  (рис. 2.8) називається скаляр, який дорівнює добутку модулів цих векторів на косинус кута між ними:
(рис. 2.8) називається скаляр, який дорівнює добутку модулів цих векторів на косинус кута між ними: .
.

 .
.
 ;
; ;
; ;
; ;
; , якщо
, якщо  ;
; ,
, 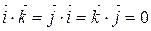 .
. та
та  , то скалярний добуток векторів можна записати у вигляді (2.15)
, то скалярний добуток векторів можна записати у вигляді (2.15)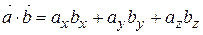 .
.
 ;
;
 ;
;
 ;
;
 .
.
 , який задовольняє умови:
, який задовольняє умови: такий, що він перпендикулярний до площини, в якій лежать вектори
такий, що він перпендикулярний до площини, в якій лежать вектори  ;
; .
.

 ;
;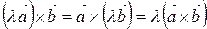 ;
; ;
; ;
; , якщо
, якщо  ;
; ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.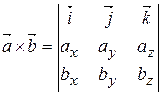 .
.
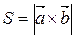 ;
;
 ;
;
 ;
;
 .
.
 .
.

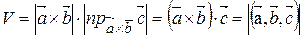
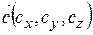 , то змішаний добуток векторів можна записати у вигляді
, то змішаний добуток векторів можна записати у вигляді .
.
 ;
; ;
; ;
; , якщо вектори
, якщо вектори 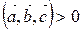 , якщо вектори
, якщо вектори  , якщо вектори
, якщо вектори  ;
;
 ;
;
 ;
;
 .
.
 . Необхідно:
. Необхідно: у просторі.
у просторі. та
та 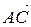 .
. на напрям вектора
на напрям вектора  .
. і до
і до  .
. .
.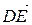 .
.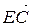 .
. до однієї площини.
до однієї площини. (0; 0; -1)
(0; 0; -1)
 називається рівнянням лінії, якщо його задовольняють усі точки, що лежать на даній лінії, і не задовольняє жодна точка, що не лежить на даній лінії. Найпростішою у певному розумінні лінією є пряма.
називається рівнянням лінії, якщо його задовольняють усі точки, що лежать на даній лінії, і не задовольняє жодна точка, що не лежить на даній лінії. Найпростішою у певному розумінні лінією є пряма. та перпендикулярно вектору
та перпендикулярно вектору  :
: .
.
 (рис. 3.1) на площині можна задати за допомогою нормального вектора
(рис. 3.1) на площині можна задати за допомогою нормального вектора 
 .
.
 рівняння (3.2) має вид
рівняння (3.2) має вид 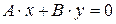 , тобто пряма проходить через початок координат;
, тобто пряма проходить через початок координат; рівняння (3.2) має вид
рівняння (3.2) має вид  , тобто пряма паралельна осі
, тобто пряма паралельна осі  ;
;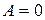 рівняння (3.2) має вид
рівняння (3.2) має вид 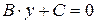 , тобто пряма паралельна осі
, тобто пряма паралельна осі  ;
;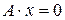 , тобто отримаємо рівняння осі
, тобто отримаємо рівняння осі  , тобто отримаємо рівняння осі
, тобто отримаємо рівняння осі  ;
;
 .
.
 , який паралельний даній прямій.
, який паралельний даній прямій.
 та
та 

 .
.

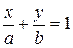 ,
де
,
де 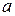 та
та  – відрізки, які відсікає пряма від координатних осей
– відрізки, які відсікає пряма від координатних осей  та
та 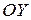 відповідно.
відповідно.
 ,
,
 – кутовий коефіцієнт прямої,
– кутовий коефіцієнт прямої,  .
.
 ,
,
 – відстань від початку координат до прямої;
– відстань від початку координат до прямої;  – кути, які створює нормаль проведена з початку координат з осями
– кути, які створює нормаль проведена з початку координат з осями  .
. ,
,
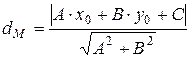


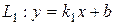


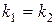


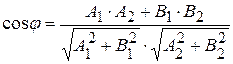

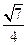 .
.
 знайти точку, відстань якої від директриси дорівнює 10.
знайти точку, відстань якої від директриси дорівнює 10.
 і має центр у точці А(-1;-3).
і має центр у точці А(-1;-3).
 ;0) та В(
;0) та В( ;1) лежать на гіперболі.
;1) лежать на гіперболі.
 .
.
 і має центр у точці А(0;-3).
і має центр у точці А(0;-3).
 ).
).
 і має центр у точці А(0;-8).
і має центр у точці А(0;-8).



