
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выражение скалярного произведения через координаты сомножителейСодержание книги
Поиск на нашем сайте
Пусть заданы два вектора Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения орт Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример 1. Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2), С(2;5;1), D(3;-2;2), взаимно перпендикулярны. Решение: Составим вектора Отсюда следует, что
Некоторые приложения скалярного произведения Угол между векторами Определение косинуса угла
Отсюда следует условие перпендикулярности двух ненулевых векторов:
Проекция вектора на заданное направление Нахождение проекции вектора
Векторное произведение и его свойства
Опр:Три некомпланарных вектора
Опр: Векторным произведением вектора · перпендикулярен векторам · имеет длину, численно равную площади параллелограмма, построенного на векторах · векторы Векторное произведение обозначается
Свойства векторного произведения
1..При перестановке сомножителей векторное произведение меняет знак, т. е. 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. 3. 4. Если два ненулевых вектора коллинеарны, то их векторное произведение равно нулю, и наоборот, из равенства нулю векторного произведения следует коллинеарность векторов. 5.
Выражение векторного произведения через координаты сомножителей Пусть даны два вектора Найдем их векторное произведение, перемножая их как многочлены, используя свойства векторного произведения:
Полученную формулу можно записать еще короче
Приложения векторного произведения Площадь параллелограмма и треугольника Площадь параллелограмма равна модулю векторного произведения двух его смежных сторон: Площадь треугольника, построенного на двух сторонах равна половине модуля векторного произведения: Условие коллинеарности векторов Если
Смешанное произведение векторов Рассмотрим произведение векторов  Смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку. Смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер. 2. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении меняющей у произведения знак. 3.Смешанное произведение ненулевых векторов
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.008 с.) |

 и
и  . Составим таблицу скалярных произведений орт:
. Составим таблицу скалярных произведений орт:

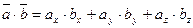
 и
и  , лежащие на диагоналях данного четырехугольника. Имеем:
, лежащие на диагоналях данного четырехугольника. Имеем: 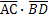 =36-36-0=0.
=36-36-0=0. . Т.е. диагонали четырехугольника ABCD взаимно перпендикулярны.
. Т.е. диагонали четырехугольника ABCD взаимно перпендикулярны. между двумя ненулевыми векторами:
между двумя ненулевыми векторами:

 в направлении
в направлении  :
:

 , взятые в указанном порядке, образуют правую тройку, если из конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если из конца третьего вектора  кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  , где
, где  образуют правую тройку.
образуют правую тройку. или
или  . Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами:
. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами:
 .
. .
. .
.

 и
и  .
. +
+

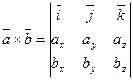 =
= 
 ,
,
 то
то  и наоборот, т.е.
и наоборот, т.е. 
 и
и  . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число. Обозначается смешанное произведение:
. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число. Обозначается смешанное произведение: 
 .
. ,
,  .
.


