Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости, проходящей через данную точку перпендикулярно данному векторуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опр.: Нормалью к плоскости называется вектор, перпендикулярный к данной плоскости.
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку Предположим, что такая плоскость построена, возьмем на ней произвольную точку М(x,y,z). Составим вектор
Данный способ задания плоскости называется плоскость по точке М
Пример: Составить уравнение плоскости, проходящей через точку А(1,2,-3), параллельно плоскости 3x-4y+5z-2=0 Решение: Выпишем нормаль к плоскости, т.е. вектор перпендикулярный плоскости: Ответ: 3x-4y+5z+20=0.
Особенности в расположении плоскостей Рассмотрим общее уравнение плоскости: Ax+ By+ Cz+ D=0. В зависимости от коэффициентов A, B, C, D плоскость может принимать следующие положения: 1. Если D=0, то плоскость Ax+By+Cz=0 проходит через начало координат, т.е. точка О(0,0,0) принадлежит плоскости, так как ее координаты удовлетворяют уравнению плоскости. 2. Если А=0, то имеем уравнение плоскости By+Cz+D = 0, нормальный вектор 3. Если А=0 и D=0, то плоскость By+Cz =0 содержит точку О(0,0,0) и параллельна оси ОХ, следовательно плоскость содержит ось ОХ. 4. Если А=0 и В=0, то Cz+D=0, или z = Ах+D=0 плоскость параллельна YOZ, а By+D=0 плоскость параллельна XOZ.
5. Плоскости координат имеют уравнения: XOY задается уравнением: Z=0, XOZ (Y=0), YOZ (X=0)
Уравнение плоскости, проходящей через данную точку, параллельно двум неколлинеарным векторам
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку
Данный способ задания плоскости называется плоскость по точке
Уравнение плоскости, проходящей через три заданные точки
Считаем, что такая плоскость построена, составим два вектора Эти векторы являются направляющими векторами плоскости. Составим уравнение плоскости по точке
Данный способ задания плоскости называется плоскость по трем точкам. Пример: Составить уравнение плоскости АВС, если даны координаты точек:
Решение: Составим уравнение плоскости
Найдем разложение определителя по первой строке:
Ответ:
Уравнение плоскости в отрезках Пусть необходимо составить уравнение плоскости, отсекающей на осях координат OX, OY, OZ соответственно отрезки a,b,c, т.е. плоскость проходит через точки A(a,0,0), B(0,b,0) и C(0,0,c).
Основные задачи Угол между плоскостями Пусть заданы две плоскости
Углом между плоскостями называется один из двухгранных углов, образованных при пересечении этих плоскостей. Выпишем нормали к плоскостям:
Условие перпендикулярности плоскостей:
Условие параллельности плоскостей:
Расстояние от точки до плоскости
Прямая линия в пространстве Общее уравнение прямой Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Пусть заданы две плоскости: Если они не параллельны, т.е. координаты нормалей к плоскостям определяет прямую линию
Уравнение прямой, проходящей через заданную точку, параллельно данному вектору
Пусть необходимо составить уравнение прямой Вектор
Данный способ задания прямой называется прямая по точке
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.006 с.) |


 и перпендикулярной вектору
и перпендикулярной вектору  .
.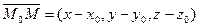 . Вектор
. Вектор 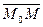 перпендикулярен вектору
перпендикулярен вектору 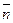 , следовательно, их скалярное произведение равно нулю:
, следовательно, их скалярное произведение равно нулю:  , это условие имеет вид::
, это условие имеет вид::
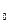 (
(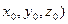 и нормали
и нормали  . Так как необходимо построить плоскость параллельную данной, то можно использовать вектор
. Так как необходимо построить плоскость параллельную данной, то можно использовать вектор  после преобразования получим: 3x-4y+5z+20=0
после преобразования получим: 3x-4y+5z+20=0 перпендикулярен оси ОХ, следовательно, плоскость параллельна оси ОХ.
перпендикулярен оси ОХ, следовательно, плоскость параллельна оси ОХ.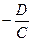 плоскость параллельна плоскости ХОУ, аналогично
плоскость параллельна плоскости ХОУ, аналогично
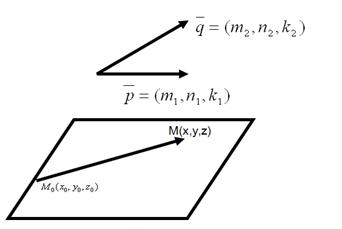 Опр.: Два неколлинеарных вектора, параллельные плоскости, называются направляющими векторами этой плоскости.
Опр.: Два неколлинеарных вектора, параллельные плоскости, называются направляющими векторами этой плоскости.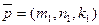 и
и  . Считаем, что такая плоскость построена, возьмем произвольную точку М(x,y,z) этой плоскости и составим вектор
. Считаем, что такая плоскость построена, возьмем произвольную точку М(x,y,z) этой плоскости и составим вектор 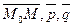 компланарны, т.е. их смешанное произведение равно 0. Запишем это условие в векторной форме:
компланарны, т.е. их смешанное произведение равно 0. Запишем это условие в векторной форме: 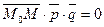 . Запишем в координатной форме:
. Запишем в координатной форме:
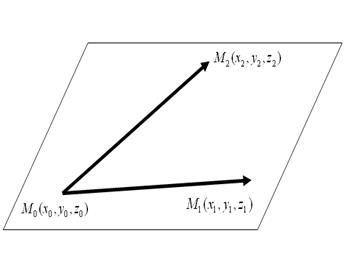 Пусть необходимо составить уравнение плоскости, проходящей через три заданные, не лежащие на одной прямой, точки:
Пусть необходимо составить уравнение плоскости, проходящей через три заданные, не лежащие на одной прямой, точки: 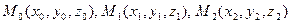
 и
и 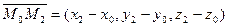 .
.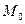 и двум направляющим векторам
и двум направляющим векторам  .
.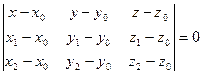
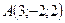 ;
; 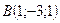 ;
; 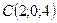
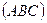 по трем точкам:
по трем точкам: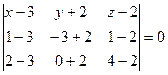 ,
,  ,
,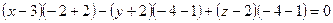 ,
, ,
,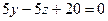 , разделим уравнение на 5:
, разделим уравнение на 5: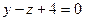 .
. Подставим координаты этих точек в уравнение плоскости по трем точкам:
Подставим координаты этих точек в уравнение плоскости по трем точкам: 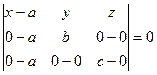 ,
, 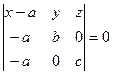 , преобразуем определитель, получим:
, преобразуем определитель, получим: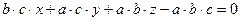 или
или 
 разделим уравнение на abc, получим:
разделим уравнение на abc, получим: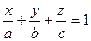
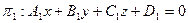
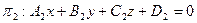 .
.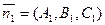 и
и  . Угол между плоскостями равен углу между нормалями к плоскостям, т.е.
. Угол между плоскостями равен углу между нормалями к плоскостям, т.е.  Косинус угла между плоскостями вычисляется по формуле:
Косинус угла между плоскостями вычисляется по формуле:
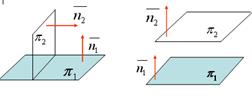
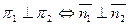 , это условие в векторной форме:
, это условие в векторной форме: 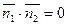 , или в координатной форме:
, или в координатной форме: 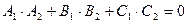
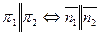 , или в координатной форме: координаты векторов должны быть пропорциональны:
, или в координатной форме: координаты векторов должны быть пропорциональны: 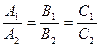
 Пусть задана точка:
Пусть задана точка: 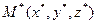 и плоскость:
и плоскость:  расстояние d от точки до плоскости находится по формуле:
расстояние d от точки до плоскости находится по формуле: 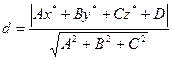
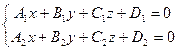
 в пространстве. Такой способ задания называют общим уравнением прямой.
в пространстве. Такой способ задания называют общим уравнением прямой.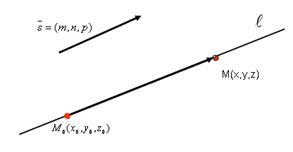
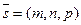 .Возьмем произвольную точку М(x,y,z) на прямой
.Возьмем произвольную точку М(x,y,z) на прямой 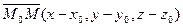 параллелен вектору
параллелен вектору 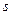 , следовательно, их координаты пропорциональны:
, следовательно, их координаты пропорциональны: