
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определителей второго и третьего порядкаСодержание книги
Поиск на нашем сайте Определители Вычисление определителей второго и третьего порядка Квадратной матрице А 1. 2. det А
3. detА
Пример: Вычислить определители матриц А= Решение: Det А= Det В= Ответ: detA=14, detB=0.
Разложение определителя матрицы по элементам строки или столбца Опр: Минором Опр: Алгебраическим дополнением
Теорема: Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.
Разложение определителя по любой (i-й, где i=1,2,…n) строке: det Разложение определителя по любому (j-му, где j=1,2,…n) столбцу: detA
Пример: Найти минор Решение:
Найдем алгебраическое дополнение: Ответ: Пример: Вычислить определитель матрицы А= Решение: Вычислим определитель разложением по третьему столбцу:
Ответ: detA=-24
Свойства определителя: 1. Определитель матрицы равен определителю транспонированной матрицы. det A=detA 2. При перестановке местами двух параллельных строк или столбцов определитель меняет свой знак на противоположный. 3. Определитель, имеющий две одинаковые, или две пропорциональные строки или столбца равен нулю. 4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя, т.е. 5. Определитель, имеющий нулевую строку или столбец равен нулю. 6. Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на любое число. Это утверждение верно и для столбцов.
Обратная матрица Опр: Квадратная матрица А называется невырожденной, если ее определитель не равен нулю, т.е. det A Опр: Матрицей, обратной к матрице А называется такая матрица Все матрицы: А, Всякая невырожденная матрица имеет обратную, которая может быть найдена по формуле:
Правило вычисления обратной матрицы: 1. Вычислить определитель матрицы detA (detA 2. Составить матрицу из алгебраических дополнений элементов: 3. Каждый элемент полученной матрицы разделить на определитель: 4. Транспонировать полученную матрицу: 5. Результат проверить, умножив А на
Пример: Для матрицы А= Решение: 1. Находим detA= 2. Составляем матрицу 3. Делим элементы на определитель: 4. Транспонируем полученную матрицу: 5. Проверка: Ответ: Пример: Для матрицы А= Решение: Находим detA= Составляем матрицу
Делим элементы на определитель: Транспонируем полученную матрицу: Проверка: Ответ: Метод Гаусса решения систем линейных уравнений Метод Гаусса является одним из наиболее универсальных и эффективных методов решения систем линейных алгебраических уравнений. Он применим как для решения системы линейных алгебраических уравнений с невырожденной матрицей, так и для систем с вырожденной матрицей и для систем, число уравнений которых не совпадает с числом переменных. Идея метода Гаусса состоит в том, что систему m линейных алгебраических уравнений относительно n неизвестных
приводят с помощью эквивалентных преобразований, не меняющих решения системы, к ступенчатому виду(в частности, к верхнетреугольному)
решение которой находят следующим образом: выражают Решение однородных систем Система линейных уравнений называется однородной, если правые части уравнений равны нулю:
Матричный вид однородной системы: Ax=0. Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной. Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю. Линейная комбинация решений однородной системы также является решением этой системы. Пример: Исследовать однородную систему на совместность, найти решения: Решение: Расширенную матрицу системы приведем к ступенчатому виду:
Система имеет множество решений.
Из второго уравнения находим Общее решение системы:
Для нахождения частных решений, свободным переменным даем произвольные значения:
Элементы векторной алгебры Векторы Величины, которые полностью определяются своим численным значением, называются скалярными. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Вектор -это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А- начало вектора, а В- его конец, то вектор обозначается символом Длиной или модулем вектора Векторы Коллинеарные векторы могут быть направлены одинаково, т.е. быть сонаправленными ( Нулевой вектор считается коллинеарным любому вектору. Два вектора Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора перемешать в любую точку пространства. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или хотя бы два коллинеарные, то такие векторы будут компланарны. Разность векторов
Если совместить начала двух векторов
Отметим, что в параллелограмме, построенном на векторах
Умножение вектора на число
· · · Линейные операции над векторами обладают следующими свойствами: 1. 2. 3. 4. Эти свойства позволяют производить преобразования в линейных операциях с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
Проекция вектора на ось Пусть в пространстве задана ось Проекцией точки М на ось Если точка М и ось Если точка М лежит на оси Пусть Проекцией вектора на ось называется число:
Свойства проекций: Проекция вектора
1. Проекции равных векторов на одну и ту же ось равны между собой. 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось. 3. При умножении вектора на число, его проекция также умножается на это число. Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Линейные операции над векторами, заданными в координатной форме: Пусть заданы два вектора: 1. 2. 3. Условие коллинеарности векторов: Док-во:Так как условие параллельности векторов
Произведения векторов Прямая на плоскости Линия на плоскости Линия на плоскости рассматривается, как множество точек, обладающих только им присущим геометрическим свойством. Введение декартовой системы координат на плоскости позволяет определить положение произвольной точки ее координатами, а положение линии на плоскости определяется с помощью уравнения. Если уравнение линии имеет вид F(x,y)=0, то любой паре чисел (x,y), удовлетворяющей данному уравнению, соответствует точка М(х,у), принадлежащая линии, и наоборот, координаты любой точки линии обращают ее уравнение в верное тождество. Если две линии на плоскости заданы своими уравнениями Решениям системы соответствуют координаты точки пересечения заданных линий. Простейшей из линий является прямая.
Уравнение прямой в отрезках
Подставим координаты этих точек в уравнение прямой, проходящей через две точки,
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат.
Угол между прямыми При пересечении двух прямых образуются четыре угла:, тангенс и косинус которых отличаются знаком. Приведены формулы для вычисления острого угла между прямыми. Если две прямые заданы своими общими уравнениеми:
Условие перпендикулярности: Условие параллельности: Если две прямые заданы уравнениями с угловыми коэффициентами:
Точка пересечения прямых Пусть две прямые заданы своими общими уравнениями:
Чтобы найти общую точку, необходимо решить систему двух уравнений с двумя переменными.
Проекция точки на прямую Пусть необходимо спроектировать точку
Пример: Даны вершины треугольника 1) уравнение высоты, опущенной из вершины 2) точку пересечения высоты 3) точку пересечения медиан треугольника Решение: 1) Составим уравнение высоты
Ответ: 2) Составим уравнение стороны
Найдем точку пересечения высоты
Ответ: N 3) Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем точку О пересечения найденных медиан:
Ответ: О
Плоскость Общее уравнение плоскости Алгебраическое уравнение первой степени в пространстве определяет плоскость. Общее уравнение плоскости можно записать в виде: Ax+ By+ Cz+ D=0 Любую плоскость можно представить в виде такого уравнение единственным способом. с точностью до коэффициента (т. е. при умножении уравнения на число, полученное уравнение задает ту же плоскость) Плоскость в пространстве можно задать различными способами, рассмотрим некоторые из них:
Основные задачи Угол между плоскостями Пусть заданы две плоскости
Углом между плоскостями называется один из двухгранных углов, образованных при пересечении этих плоскостей. Выпишем нормали к плоскостям:
Условие перпендикулярности плоскостей:
Условие параллельности плоскостей:
Расстояние от точки до плоскости
Прямая линия в пространстве Общее уравнение прямой Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Пусть заданы две плоскости: Если они не параллельны, т.е. координаты нормалей к плоскостям определяет прямую линию
Уравнение прямой, проходящей через заданную точку, параллельно данному вектору
Пусть необходимо составить уравнение прямой Вектор
Данный способ задания прямой называется прямая по точке
Кривые второго порядка Алгебраическое уравнение второго порядка на плоскости описывает кривую второго порядка, другими словами, любое уравнение вида Эллипс
Полуосями этого эллипса являются по оси ОХ- отрезок а, и по оси ОУ- отрезок b. Таким образом, эллипс имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с координатами (-а;0); (а;0); (0;-b); (0;b). Если величина а Характеристическое свойство эллипса: Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, постоянна и равна удвоенной большей полуоси.
-каноническое уравнение эллипса, центр симметрии которого находится в точке Q( полуоси эллипса: по ОХ равна a, по оси ОУ равна b. Фокусы находятся в точках: Пример: Построить эллипс, каноническое уравнение которого:
Решение: Центром симметрии эллипса является точка Q(2; -3), полуоси эллипса: а=3; b=2;
Гипербола Каноническое уравнение гиперболы, с центром в начале координат:
Полуосями этой гиперболы являются по оси ОХ- отрезок а, и по оси ОУ- отрезок b. Таким образом, гипербола имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с координатами (-а;0); (а;0); (0;-b); (0;b). Если величина Гипербола имеет две асимптоты, уравнения которых:
Гиперболой, сопряженной к данной, называется гипербола:
Для этой гиперболы а- мнимая полуось, b-действительная.
Характеристическое свойство гиперболы: гиперболой называется геометрическое место точек, модуль разности расстоян
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 порядка n можно поставить в соответствие число, обозначаемое det А (или
порядка n можно поставить в соответствие число, обозначаемое det А (или  или
или  ), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам:
), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам: det А
det А  =
= 
 =
=  = +=
= += 
 =
=  =
=  = =
= =  -
- 
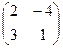 , В=
, В= 


 элемента
элемента  определителя n-го порядка называется определитель (n-1)-го порядка,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент
определителя n-го порядка называется определитель (n-1)-го порядка,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент  элемента
элемента 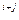 :
: 


 и алгебраическое дополнение
и алгебраическое дополнение  элемента
элемента 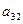 матрицы А=
матрицы А=  .
.
 =
=  =0+0+2-15-8-0=-21;
=0+0+2-15-8-0=-21;
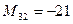 ,
, 

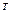 .
.

 , которая удовлетворяет условиям:
, которая удовлетворяет условиям:  .
. , где
, где  алгебраическое дополнение элемента
алгебраическое дополнение элемента 




 .
. найти обратную.
найти обратную.
 , поэтому
, поэтому 

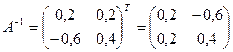


 найти обратную.
найти обратную.


 поэтому
поэтому 





 :
:

 ,
, .из последнего уравнения, подставляют в предпоследнее, из которого выражается
.из последнего уравнения, подставляют в предпоследнее, из которого выражается 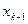 и т.д., из первого уравнения выражается
и т.д., из первого уравнения выражается  .
.








 восстановим систему:
восстановим систему: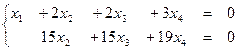
 главные переменные,
главные переменные,  и
и  свободные переменные. Перенесем свободные переменные в правые части уравнений.
свободные переменные. Перенесем свободные переменные в правые части уравнений.
 подставляя это выражение в первое уравнение, получим:
подставляя это выражение в первое уравнение, получим: 




 , или
, или  . Вектор
. Вектор  (у него начало в точке В, а конец в точке А) называется противоположным вектору
(у него начало в точке В, а конец в точке А) называется противоположным вектору  .
. . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора
. Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора  .
. называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы 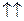
 ).
).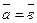 ), если они коллинеарные, одинаково направлены и имеют одинаковые длины.
), если они коллинеарные, одинаково направлены и имеют одинаковые длины. Под разностью векторов
Под разностью векторов  такой, что
такой, что 
 Произведением вектора
Произведением вектора  называется вектор
называется вектор  , который удовлетворяет следующим условиям:
, который удовлетворяет следующим условиям:
 , т.е. векторы
, т.е. векторы  , если
, если  ,
,  если
если 




 , т. е. направленная прямая.
, т. е. направленная прямая.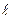 с плоскостью, проходящей через точку М перпендикулярно оси
с плоскостью, проходящей через точку М перпендикулярно оси  произвольный вектор (
произвольный вектор ( ). Обозначим через
). Обозначим через  и
и  проекции на ось l соответственно начала А и конца В вектора
проекции на ось l соответственно начала А и конца В вектора 
 , если
, если  сонаправлены,
сонаправлены, , если
, если  , если
, если  , или
, или  .
.
 На рисунке
На рисунке  <
<  .
. отрицательна, т.к.
отрицательна, т.к.  .
.

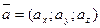 и
и  , тогда:
, тогда:


 - т.е. проекции коллинеарных векторов пропорциональны.
- т.е. проекции коллинеарных векторов пропорциональны. можно записать в виде:
можно записать в виде:  , откуда
, откуда  , таким образом, условие коллинеарности в координатном виде:
, таким образом, условие коллинеарности в координатном виде:  , то задача о пересечении этих линий сводится к решению системы двух уравнений с двумя переменными:
, то задача о пересечении этих линий сводится к решению системы двух уравнений с двумя переменными: 
 Пусть прямая пересекает ось Ох в точке
Пусть прямая пересекает ось Ох в точке  , а ось Оу - в точке
, а ось Оу - в точке  .
. После преобразований получим:
После преобразований получим:
 , нормаль к прямой
, нормаль к прямой  :
: 
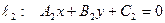 , нормаль к прямой
, нормаль к прямой  :
: 
 Угол между прямыми есть угол между нормалями к прямым
Угол между прямыми есть угол между нормалями к прямым 



 ,
, то вычисляется тангенс угла между прямыми:
то вычисляется тангенс угла между прямыми: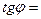



 , если система несовместна, то прямые параллельны.
, если система несовместна, то прямые параллельны. на прямую
на прямую  Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор
Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор  . Составим уравнение проецирующей прямой. Она проходит через точку
. Составим уравнение проецирующей прямой. Она проходит через точку 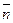 . Подставив координаты точки и вектора в каноническое уравнение прямой
. Подставив координаты точки и вектора в каноническое уравнение прямой  , получим:
, получим:  . Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему:
. Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему:  решение этой системы есть координаты точки, являющейся проекцией точки
решение этой системы есть координаты точки, являющейся проекцией точки 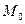 на прямую
на прямую  :
:  ;
; 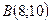 ;
;  . Найти:
. Найти: ;
; и стороны
и стороны  ;
; :
: ;
;  ,
,  .
. ,
,  ,
,  ,
, .
.



 .
. :
: ,
,  ,
,  ,
,  .
. :
: ,
,  ,
,  ,
, .
. :
: ,
, 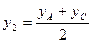 .
. ,
,  .
.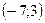 :
: ,
,  ,
,  ,
,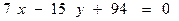 .
.


 .
.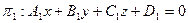
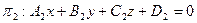 .
.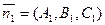 и
и  . Угол между плоскостями равен углу между нормалями к плоскостям, т.е.
. Угол между плоскостями равен углу между нормалями к плоскостям, т.е.  Косинус угла между плоскостями вычисляется по формуле:
Косинус угла между плоскостями вычисляется по формуле:
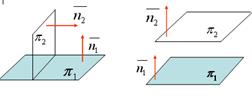
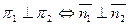 , это условие в векторной форме:
, это условие в векторной форме: 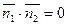 , или в координатной форме:
, или в координатной форме: 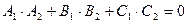
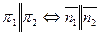 , или в координатной форме: координаты векторов должны быть пропорциональны:
, или в координатной форме: координаты векторов должны быть пропорциональны: 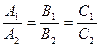
 Пусть задана точка:
Пусть задана точка: 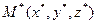 и плоскость:
и плоскость:  расстояние d от точки до плоскости находится по формуле:
расстояние d от точки до плоскости находится по формуле: 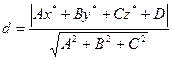
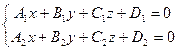
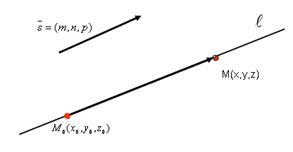
 , параллельно заданному вектору
, параллельно заданному вектору 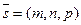 .Возьмем произвольную точку М(x,y,z) на прямой
.Возьмем произвольную точку М(x,y,z) на прямой 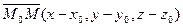 параллелен вектору
параллелен вектору 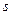 , следовательно, их координаты пропорциональны:
, следовательно, их координаты пропорциональны: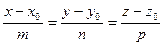
 определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет.
определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет. Каноническое уравнение эллипса, с центром в начале координат:
Каноническое уравнение эллипса, с центром в начале координат: 
 b, то
b, то  . На большей оси в точках с координатами
. На большей оси в точках с координатами  и
и  (с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется
(с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется 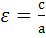 ,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса
,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса 

 ,
,
 ,найти его фокусы и эксцентриситет.
,найти его фокусы и эксцентриситет. ; фокусы эллипса находятся в точках:
; фокусы эллипса находятся в точках:  .
.


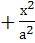 , то полуось а называется действительной, b-мнимой.
, то полуось а называется действительной, b-мнимой.  . На продолжении действительной оси в точках с координатами
. На продолжении действительной оси в точках с координатами 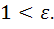


 . Фокусы находятся в точках:
. Фокусы находятся в точках:  и
и 



