
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение прямой и плоскостиСодержание книги
Поиск на нашем сайте
Пусть плоскость Подставляя выражения для x,y и z в уравнение плоскости: · данное уравнение имеет единственное решение, то прямая и плоскость пересекаются и для нахождения точки пересечения, необходимо найденное значение параметра t подставить в параметрическое уравнение прямой · если уравнение решения не имеет, то прямая параллельна плоскости · если решений множество, т.е. уравнение верно при любом t, то прямая принадлежит плоскости.
Кривые второго порядка Алгебраическое уравнение второго порядка на плоскости описывает кривую второго порядка, другими словами, любое уравнение вида Эллипс
Полуосями этого эллипса являются по оси ОХ- отрезок а, и по оси ОУ- отрезок b. Таким образом, эллипс имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с координатами (-а;0); (а;0); (0;-b); (0;b). Если величина а Характеристическое свойство эллипса: Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, постоянна и равна удвоенной большей полуоси.
-каноническое уравнение эллипса, центр симметрии которого находится в точке Q( полуоси эллипса: по ОХ равна a, по оси ОУ равна b. Фокусы находятся в точках: Пример: Построить эллипс, каноническое уравнение которого:
Решение: Центром симметрии эллипса является точка Q(2; -3), полуоси эллипса: а=3; b=2;
Гипербола Каноническое уравнение гиперболы, с центром в начале координат:
Полуосями этой гиперболы являются по оси ОХ- отрезок а, и по оси ОУ- отрезок b. Таким образом, гипербола имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с координатами (-а;0); (а;0); (0;-b); (0;b). Если величина Гипербола имеет две асимптоты, уравнения которых:
Гиперболой, сопряженной к данной, называется гипербола:
Для этой гиперболы а- мнимая полуось, b-действительная.
Характеристическое свойство гиперболы: гиперболой называется геометрическое место точек, модуль разности расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами постоянна и равна удвоенной действительной полуоси.
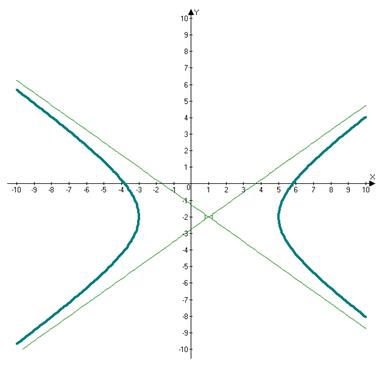
-каноническое уравнение гиперболы, центр симметрии которого находится в точке Q( полуоси гиперболы: действительная по ОХ равна a, мнимая по оси ОУ равна b. Фокусы находятся в точках: Пример: Построить гиперболу, каноническое уравнение которой:
найти фокусы и эксцентриситет.
Решение: центр симметрии гиперболы находится в точке:Q(1,-2), действительная полуось а=4; мнимая полуось b=3.
Фокусы: Эксцентриситет:
Парабола Каноническое уравнение параболы с вершиной в начале координат:
Характеристическое свойство параболы: параболой называется геометрическое место точек, равноудаленных от точки, называемой фокусом и от прямой, называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается Вершина параболы находится посередине между фокусом и директрисой. Фокус находится на оси симметрии внутри параболы, для данной параболы F(
Пример: Построить параболу, определить ее фокус и директрису: -4·(x-4)=(y+3)² Решение: Уравнение параболы в общем виде: 2· p·(x-a)=(y-b)² В нашем уравнении: a=4,b=-3, 2p=4, p=2. Фокус: F(a-p/2;b)=F(3;-3) Директриса x=p/2+a x=5. Вершина параболы находится в точке Q(4; -3),
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 задана своим общим уравнением: Ax+By+Cz+D=0, а прямая
задана своим общим уравнением: Ax+By+Cz+D=0, а прямая 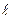 в каноническом виде:
в каноническом виде: 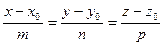 . Для решения этой задачи проще всего: прямую представить в параметрическом виде:
. Для решения этой задачи проще всего: прямую представить в параметрическом виде:  где
где 
 , если:
, если: определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет.
определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет. Каноническое уравнение эллипса, с центром в начале координат:
Каноническое уравнение эллипса, с центром в начале координат: 
 b, то
b, то  . На большей оси в точках с координатами
. На большей оси в точках с координатами  и
и  (с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется
(с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется 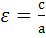 ,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса
,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса 

 ,
,
 ,найти его фокусы и эксцентриситет.
,найти его фокусы и эксцентриситет. ; фокусы эллипса находятся в точках:
; фокусы эллипса находятся в точках:  .
.


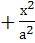 , то полуось а называется действительной, b-мнимой.
, то полуось а называется действительной, b-мнимой.  . На продолжении действительной оси в точках с координатами
. На продолжении действительной оси в точках с координатами 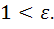


 . Фокусы находятся в точках:
. Фокусы находятся в точках:  и
и 
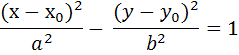


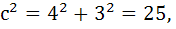 с=5.
с=5.
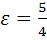 =1,25.
=1,25.



 .
. перпендикулярна оси симметрии, находится вне параболы, ее уравнение х =
перпендикулярна оси симметрии, находится вне параболы, ее уравнение х =  .
.



