Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поток вектора электрического смещения. Теорема Остроградского-Гаусса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ 1. Электрический заряд. Дискретность. Закон сохранения. Закон Кулона. Вектор напряженности электрического поля. Электрическое поле точечного заряда. Принцип суперпозиции. Графическое изображение (примеры). Свойства силовых линий. Примеры Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Существует два рода электрических зарядов, условно названных положительными и отрицательными. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются, разноименные – притягиваются. Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Электрический заряд дискретен, т. е. заряд любого тела составляет целое кратное от элементарного электрического заряда е ( Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной: q1 + q2 + q3 +... +qn = const. Закон Кулона: Сила взаимодействия между двумя точечными электрическими зарядами пропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния между ними.
где F — Сила Кулона, q1 и q2 — Электрический заряд тела, r — Расстояние между зарядами, Чтобы выполнялся закон Кулона необходимо 3 условия: 1 условие: Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров 2 условие: Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд 3 условие: Взаимодействие зарядов в вакууме В векторном виде закон записывается следующим образом:
где Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q:
Из этого определения видно, почему напряжённость электрического поля иногда называется силовой характеристикой электрического поля. В каждой точке пространства в данный момент времени существует своё значение вектора E (вообще говоря — разное в разных точках пространства), таким образом, E — это векторное поле. Формально это выражается в записи
представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как E может меняться со временем). Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл]. Обозначим: q - заряд, создающий поле, q0 - заряд, помещенный в поле (внешний заряд). Закон Кулона:
Напряженность поля:
Тогда напряженность поля точечного заряда:
Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.
Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке А поля двух точечных зарядов
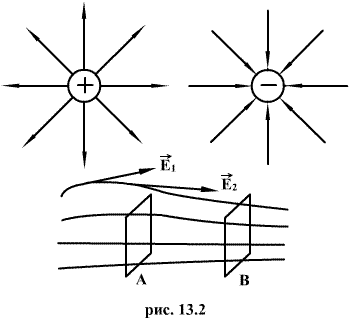
Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м2, перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.
При положительном заряде, образующем поле, вектор напряженности направлен вдоль радиуса от заряда, при отрицательном - вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.
Поле конденсатора Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля.
Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением
Вне пластин вектора
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
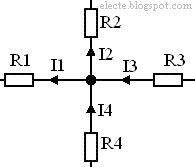
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. Конденсаторы (condensare - сгущение). Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы - лейденская банка (Мушенбрук, сер. XVII в.). Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды - конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. Законы Кирхгофа. Первый закон Кирхгофа. 1) Первый закон (правило) Кирхгофа - алгебраическая сумма токов сходящихся в узле равна нулю. Ветви - это проводящие участки цепи между узлами. Узел - это область соединения двух (или трёх) и более ветвей. Алгебраическая сумма - это значит в неё входят слагаемые со знаком плюс и со знаком минус. На рисунке ниже показан узел в котором соединяются четыре ветви с токами: I1, I2, I3, I4.
Рисунок 1 - Узел с ветвями
Ток I1 вошел в уравнение (1) со знаком минус так как этот ток направлен от узла (см. рисунок 1). Ток I2 входит в уравнение (1) со знаком минус по той же причине. Токи I3 и I4 входят в уравнение (1) со знаком плюс так как они направлены к узлу (см. рисунок 1). Вся эта алгебраическая сумма равна нулю. Токи I1 и I2 можно перенести в правую часть уравнения с противоположным знаком:
Также можно поступить и с любым уравнением записанным по первому закону Кирхгофа. Учитывая это можно дать другое определение первого закона (правила) Кирхгофа: 2) сумма токов входящих в узел равна сумме токов выходящих из него. Уравнение (2) можно привести к виду:
перенеся в правую часть уравнения токи I3 и I4 с противоположным знаком.
Тоже самое можно проделать с любым уравнением записанным по первому закону Кирхгофа. Это значит что не имеет значения то какое направление (от узла или к узлу) принято за положительное а какое за отрицательное, главное чтобы все одинаковые направления имели один знак а все противоположные другой. Иногда бывает так что один узел принимается за два и более при невнимательном осмотре схемы что приводит к ошибкам в расчётах. Рассмотрим схему на рисунке 2:
Рисунок 2 - Схема с одним узлом В этой схеме один узел, для этого узла можно составить уравнение по первому закону Кирхгофа:
МАГНИТНОЕ ПОЛЕ 1. Магнитное поле и его характеристики. Определение направления и индукции магнитного поля с помощью рамки с током. Графическое изображение. Свойства силовых линий (примеры). Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поляприводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с. Графическое изображение магнитного поля. Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец постоянного магнита, из которого выходят силовые линии (рис. 35, а), принято считать северным полюсом, а противоположный конец, в который входят силовые линии,— южным полюсом (силовые линии, проходящие внутри магнита, не показаны). Распределение силовых линий между полюсами плоского магнита можно обнаружить при помощи стальных опилок, насыпанных на лист бумаги, положенный на полюсы (рис. 35, б). Для магнитного поля в воздушном зазоре между двумя параллельно расположенными разноименными полюсами постоянного магнита характерно равномерное распределение силовых магнитных линий (рис. 36) (силовые линии, проходящие внутри магнита, не показаны).
Для более наглядного изображения магнитного поля силовые линии располагают реже или гуще. В тех местах, где магнитное роле сильнее, силовые линии располагают ближе друг к другу, там же, где оно слабее,— дальше друг от друга. Силовые линии нигде не пересекаются. Во многих случаях удобно рассматривать магнитные силовые линии как некоторые упругие растянутые нити, которые стремятся сократиться, а также взаимно отталкиваются друг от друга (имеют взаимный боковой распор). Такое механическое представление о силовых линиях позволяет наглядно объяснить возникновение электромагнитных сил при взаимодействии магнитного поля и Проводника с током, а также двух магнитных полей. Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля. Характеристикой магнитного поля является вектор магнитной индукции или индукции магнитного поля, обозначаемый В. За направление вектора магнитной индукции в данной точке поля принимают направление, в котором указывает N- полюс свободно вращающейся магнитной стрелки (рис. 2 а). Ориентацию рамки с током в магнитном поле тоже можно использовать для определения направления вектора магнитной индукции, так как её плоскость устанавливается в поле перпендикулярно вектору магнитной индукции (см. §1). При этом направление вектора магнитной индукции определяют с помощью правила правого буравчика, согласно которому, если вращать ручку буравчика по направлению тока в рамке, то сам буравчик будет перемещаться в направлении вектора магнитной индукции (рис. 2 б). Направление, в котором перемещается правый буравчик, ещё называют положительной нормалью к плоскости рамки с током. Линиями магнитной индукции называют линии, касательные к которым имеют то же направление, что и вектор магнитной индукции в этой точке поля. Линии магнитной индукции служат силовыми характеристиками поля, как и силовые линии электрического поля. Очевидно, что, как и силовые линии электрического поля, линии магнитной индукции не могут пересекаться между собой. Картину линий магнитной индукции поля можно построить с помощью магнитной стрелки или рамки с током, помещая их в различные точки поля. Как следует из опытов Эрстеда (см. §1), прямолинейный проводник с током создаёт вокруг себя магнитное поле. На рис.2 в показаны линии магнитной индукции поля прямолинейного проводника, которые представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной этому проводнику. Направление вектора магнитной индукции в этом случае можно определить опять же с помощью правого буравчика: если направление поступательного движения буравчика совпадает с направлением тока, то направление движения ручки буравчика указывает на направление вектора магнитной индукции. Видно (см. рис.2 в), что линии магнитной индукции прямолинейного проводника с током оказались замкнутыми, т.е. линиями без начала и конца. Поля, характеризуемые замкнутыми силовыми линиями, называют вихревыми. Из курса физики за 10 класс известно, что силовые линии электростатического поля всегда имеют начало и конец, начинаясь на положительных и оканчиваясь на отрицательных электрических зарядах. В отличие от электростатических все магнитные поля являются вихревыми. Замкнутость линий магнитной индукции – фундаментальное свойство магнитного поля, вызванное тем, что изолированных магнитных зарядов, подобных электрическим, не существует. Любое магнитное поле, возникающее при движении электрических зарядов, всегда содержит N и S -полюса, и сколько бы мы ни дробили постоянный магнит, каждая его песчинка всегда будет содержать разноимённые магнитные полюса.
Рис. 2. (а) – определение направления вектора магнитной индукции с помощью магнитной стрелки; (б) - применение правила буравчика для определения направления вектора магнитной индукции и положительной нормали рамки с током; (в) - применение правила буравчика для определения направления вектора магнитной индукции прямолинейного проводника с током.
Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q - заряд частицы;
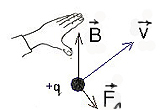
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).
и создает центростремительное ускорение равное
В этом случае частица движется по окружности.
тогда радиус окружности
а период обращения заряда в магнитном поле
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Эффект Холла. Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения поперечной разности потенциалов в полупроводнике, по которому протекает электрический ток и существует магнитное поле Н, перпендикулярное направлению тока. Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца где v –скорость носителя; q – его заряд. Направление силы Лоренца определяется правилом левой руки. Если проводник n -типа проводимости, то электроны будут смещаться влево к внешней стороне пластины, заряжая её отрицательно (рис. 6.8). В полупроводника p -типа проводимости при том же направлении тока сила Лоренца будет смещать дырки в том же направлении. При этом левая внешняя сторона пластинки зарядится положительно. Если угол между вектором скорости носителей v и вектором магнитной индукции B равен 90о, то величина силы Лоренца рассчитывается по формуле F л= qvB, (6.12) где v – средняя дрейфовая скорость носителей заряда, м/c. Электрическое поле между поперечными гранями пластинки равно где U х» (0,6…1)·10-4 В - разность потенциалов между поперечными гранями пластинки, называемая эдс Холла; а – ширина пластинки. Поле Е х действует на электроны с силой F =- qE х, направленной против силы Лоренца F л. При выполнении условия F л= F поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенства qvB = qE х следует E х= vB. Дрейфовая скорость носителей тока определяется из выражения где j – плотность тока, А/м2, n – концентрация электронов, м-3, Тогда выражение для поля Е х приобретает вид Умножив обе части равенства (6.15) на ширину пластинки а, получаем формулу для эдс Холла Формула (6.16) обычно записывается в виде где С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения где А =1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А =1,93 при рассеянии на ионизированных примесях. Для дырочных полупроводников коэффициент Холла рассчитывается по формуле где q и p –заряд и концентрация дырок, соответственно. При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле где μ n и μ p – подвижности электронов и дырок, соответственно. Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия ni = pi значение коэффициента Холла равно ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
Уравнение Максвелла. Теорию электромагнитного поля (ЭМП) Максвелл сформулировал в виде системы нескольких уравнений. В учении об электромагнетизме эти уравнения Максвелла играют такую же роль, как уравнения (или законы) Ньютона в механике. 1) Мы знаем теорему о циркуляции вектора напряжённости магнитного поля:
но:
Это уравнение является обобщением закона Био–Савара–Лапласа и показывает, что циркуляция вектора В дифференциальной форме это уравнение Максвелла выглядит так:
2) Рассматривая явление электромагнитной индукции, мы сделали вывод, что ЭДС индукции
Это уравнение описывает явление электромагнитной индукции (закон Фарадея) и устанавливает количественную связь между электрическими и магнитными полями: переменное электрическое поле порождает переменное магнитное поле. В этом физический смысл уравнения. В дифференциальной форме это уравнение выглядит так:
Различие в знаках этого уравнения Максвелла соответствует закону сохранения энергии и правилу Ленца. Если бы знаки при 3) Ещё два уравнения выражают теорему Остроградского–Гаусса для электрического и магнитного полей (статических полей)
Поток вектора электрического смещения В дифференциальной форме
4) И для магнитного поля
Это уравнение выражает то свойство магнитного поля, что линии вектора магнитной индукции В дифференциальной форме
5, 6, 7) Наконец надо помнить, что величины, входящие в эти четыре уравнения не независимы, и между ними существует связь:
здесь σ – удельная проводимость, Эти уравнения называются уравнениями состояния или материальными уравнениями. Вид этих уравнений определяется электрическими и магнитными свойствами среды. В общем случае уравнения состояния очень сложны и нелинейны. Уравнения (7.3.1 – 7.3.8) составляют полную систему уравнений Максвелла. Таким образом, полная система уравнений Максвелла в дифференциальной и интегральной формах имеет вид:
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ 1. Электрический заряд. Дискретность. Закон сохранения. Закон Кулона. Вектор напряженности электрического поля. Электрическое поле точечного заряда. Принцип суперпозиции. Графическое изображение (примеры). Свойства силовых линий. Примеры Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Существует два рода электрических зарядов, условно названных положительными и отрицательными. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются, разноименные – притягиваются. Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Электрический заряд дискретен, т. е. заряд любого тела составляет целое кратное от элементарного электрического заряда е ( Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной: q1 + q2 + q3 +... +qn = const. Закон Кулона: Сила взаимодействия между двумя точечными электрическими зарядами пропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния между ними.
где F — Сила Кулона, q1 и q2 — Электрический заряд тела, r — Расстояние между зарядами, Чтобы выполнялся закон Кулона необходимо 3 условия: 1 условие: Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров 2 условие: Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд 3 условие: Взаимодействие зарядов в вакууме В векторном виде закон записывается следующим образом:
где Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q:
Из этого определения видно, почему напряжённость электрического поля иногда называется силовой характеристикой электрического поля. В каждой точке пространства в данный момент времени существует своё значение вектора E (вообще говоря — разное в разных точках пространства), таким образом, E — это векторное поле. Формально это выражается в записи
представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как E может меняться со временем). Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл]. Обозначим: q - заряд, создающий поле, q0 - заряд, помещенный в поле (внешний заряд). Закон Кулона:
Напряженность поля:
Тогда напряженность поля точечного заряда:
Если поле образовано
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 846; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.137.209 (0.012 с.) |

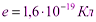 ).
).
 — Электрическая постоянная,
— Электрическая постоянная,  — Диэлектрическая проницаемость среды, k = 9*10^9 — Коэффициент пропорциональности.
— Диэлектрическая проницаемость среды, k = 9*10^9 — Коэффициент пропорциональности.
 - сила, с которой заряд 1 действует на заряд 2; q1, q2 — величина зарядов;
- сила, с которой заряд 1 действует на заряд 2; q1, q2 — величина зарядов;  — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —
— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — 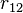 ); k — коэффициент пропорциональности.
); k — коэффициент пропорциональности.


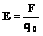 .
.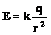


 и
и 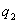 (рис. 13.1). Сложение векторов
(рис. 13.1). Сложение векторов  и
и  производится по правилу параллелограмма. Направление результирующего вектора
производится по правилу параллелограмма. Направление результирующего вектора  находится построением, а его абсолютная величина может быть подсчитана по формуле
находится построением, а его абсолютная величина может быть подсчитана по формуле


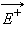 и
и  направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
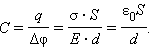

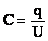 .
.




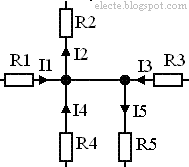
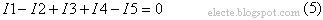 Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.
Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади. Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б).
Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б). Рис. 35. Магнитное поле, созданное постоянным магнитом.
Рис. 35. Магнитное поле, созданное постоянным магнитом.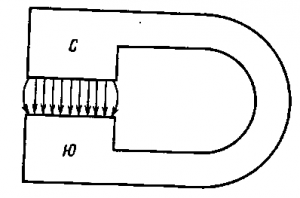 Рис. 36. Однородное магнитное поле между полюсами постоянного магнита.
Рис. 36. Однородное магнитное поле между полюсами постоянного магнита. Рис. 37. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий.
Рис. 37. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий.







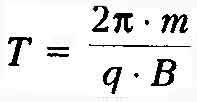
 , Н, (6.11)
, Н, (6.11) , В/м, (6.13)
, В/м, (6.13) , (6.14)
, (6.14) . (6.15)
. (6.15) ,В. (6.16)
,В. (6.16) , (6.17)
, (6.17) – коэффициент Холла, м3/Кл.
– коэффициент Холла, м3/Кл.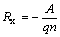 , (6.18)
, (6.18) , (6.19)
, (6.19) , (6.20)
, (6.20)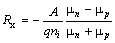 . (6.21)
. (6.21)

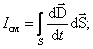
 ; т.е.
; т.е. 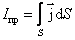 , тогда
, тогда
 по произвольному замкнутому контуру L равна сумме токов проводимости и токов смещения сквозь поверхность, натянутую на этот контур. Или другими словами, показывает связь между полным током и порождаемым им магнитным полем.
по произвольному замкнутому контуру L равна сумме токов проводимости и токов смещения сквозь поверхность, натянутую на этот контур. Или другими словами, показывает связь между полным током и порождаемым им магнитным полем.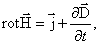 где
где 
 . Перейдем от вихревого электрического поля к магнитному:
. Перейдем от вихревого электрического поля к магнитному: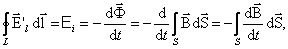
 ,
,
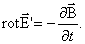
 и
и  были одинаковы, то бесконечно малое увеличение одного из полей вызвало бы неограниченное увеличение обоих полей, а бесконечно малое уменьшение одного из полей, приводило бы к полному исчезновению обоих полей. То есть различие в знаках является необходимым условием существования устойчивого ЭМП.
были одинаковы, то бесконечно малое увеличение одного из полей вызвало бы неограниченное увеличение обоих полей, а бесконечно малое уменьшение одного из полей, приводило бы к полному исчезновению обоих полей. То есть различие в знаках является необходимым условием существования устойчивого ЭМП.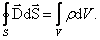 ,
,
 через замкнутую поверхность S равен сумме зарядов внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора
через замкнутую поверхность S равен сумме зарядов внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора  начинаются и заканчиваются на зарядах.
начинаются и заканчиваются на зарядах. где
где 
 ,
,
 всегда замкнуты и что магнитных зарядов нет.
всегда замкнуты и что магнитных зарядов нет.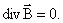 ,
,
 ,
,
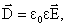 ,
,
 ,
,
 – плотность сторонних токов.
– плотность сторонних токов. ;
;  – обобщенный закон Био–Савара–Лапласа;
– обобщенный закон Био–Савара–Лапласа; ;
;  – закон Фарадея;
– закон Фарадея; ;
;  – теорема Гаусса;
– теорема Гаусса;
 – отсутствие магнитных зарядов;
– отсутствие магнитных зарядов; ,
,  ,
,