
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Напряженность электрического поляСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основные формулы и указания к решению задачи Напряженность электрического поля выражается формулой:
где Сила, действующая на точечный заряд q, помещенный в электрическое поле
Поток вектора напряженности а) через произвольную поверхность S, помещенную в неоднородное поле,
где a – угол между вектором напряженности dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль. б) через плоскую поверхность, помещенную в однородное электрическое поле, ФЕ = ЕS сos a. (2.4) Поток вектора напряженности
где интегрирование ведется по всей поверхности. Теорема Остроградского – Гаусса. Поток вектора напряженности
где n – число зарядов. Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда,
Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы: а) внутри сферы (r < R): E = 0; (2.8) б) на поверхности сферы (r = R):
в) вне сферы (r > R):
Принцип суперпозиции наложения электрических полей: напряженность
В случае двух электрических полей с напряженностями
где a – угол между векторами Напряженность поля, создаваемого бесконечно равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси,
где t – линейная плотность заряда. Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити (цилиндра):
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
где s – поверхностная плотность заряда. Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:
Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю поверхностной плотностью s заряда (например, поле плоского конденсатора)
Пример решения задачи Две концентрические проводящие сферы радиусами R 1 = 6 см и R 2 = 10 см несут соответственно заряды Q 1 = 1 нКл и Q 2 = –0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра на расстояниях r 1 = 5 см, r 2 = 9 см, r 1 = 15 см. Построить график Е (r). Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 2.1): области 1. Для определения напряженности
Рис. 2.1. Построение гауссовых поверхностей для расчета напряженностей электрического поля.
2. В области II гауссову поверхность проведем радиусом r 2. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум)):
(т.к. внутри гауссовой поверхности находится только заряд
Обозначив напряженность Е для области II через
где
3. В области III гауссова поверхность проводится радиусом r 3. Обозначим напряженность Е области III через Е 3 и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен
Заметив, что
Убедимся в том, что правая часть равенств (2.21) и (2.23) дает единицу напряженности:
Выразим все величины в единицах СИ (Q 1 = 10‑9 Кл, Q 2 = –0,5×10‑9 Кл, r 1 = 0,09 м, r 2 = 0,15 м, Е 2 = 1,11 кВ / м; Е 3 = 200 кВ / м. Построим график E (r). В области График зависимости E(r) представлен на рис. 2.2.
Рис. 2.2. График зависимости E(r) 2.3 Задание для самостоятельного выполнения по вариантам Дано n проводящих фигур (сфер, цилиндров, плоскостей) или шар из изотропного диэлектрика. Каждая фигура несет заряд, характеризующийся объемной r n, поверхностной s n или линейной t n плотностью заряда. Точки А, В, С находятся на расстояниях rА, rВ, rС от центра или оси симметрии фигуры. Взаимодействие осуществляется в вакууме. Данные для решение задач приведены в табл. 2.1 и на рис. 2.3. Фигуре с номером 1 соответствуют размеры R 1 и величины s1, r1, t1 и т.д. (рис. 2.3). Если в строке табл. 2.1 с номером вашего варианта какие-то клетки не заполнены, значит для решения вашей задачи эти данные не нужны. 1. Используя теорему Остроградского-Гаусса и принцип суперпозиции электростатических полей, найти зависимость напряженности электрического поля от расстояния Е (r) для всех областей (внутри фигуры, между фигурами и вне фигур). 2. Сделать схематический рисунок и показать направление вектора Е в каждой области. 3. Вычислить напряженность Е в точках А, В, С удаленных от центра симметрии фигур на расстояния ri. 4. Построить график зависимости Е (r) для всех областей.
Данные для выполнения задания. Таблица 2.1
Окончание таблицы 2.1
Рис. 2.3. Схемы расположения фигур
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.011 с.) |

 , (2.1)
, (2.1) – сила, действующая на точечный положительный заряд q, помещенный в данную точку поля.
– сила, действующая на точечный положительный заряд q, помещенный в данную точку поля. . (2.2)
. (2.2) электрического поля:
электрического поля:
 или
или  , (2.3)
, (2.3) к элементу поверхности;
к элементу поверхности;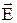 через замкнутую поверхность
через замкнутую поверхность , (2.5)
, (2.5) , (2.6)
, (2.6) – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности;
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; . (2.7)
. (2.7) ; (2.9)
; (2.9) . (2.11)
. (2.11)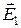 и
и  модуль вектора напряженности
модуль вектора напряженности , (2.12)
, (2.12) , (2.13)
, (2.13) . (2.14)
. (2.14) , (2.15)
, (2.15) . (2.16)
. (2.16) . (2.17)
. (2.17)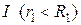 , области
, области  , области
, области 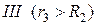 .
. в области I проведем гауссову поверхность
в области I проведем гауссову поверхность  радиусом r 1 и воспользуемся теоремой Остроградского–Гаусса:
радиусом r 1 и воспользуемся теоремой Остроградского–Гаусса:  (т.к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии
(т.к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии  Следовательно,
Следовательно,  и
и  , будет равна нулю, т.е. Е 1 = 0.
, будет равна нулю, т.е. Е 1 = 0.
 (2.18)
(2.18) ). Из соображения симметрии
). Из соображения симметрии 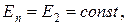 то Е можно вынести за знак интеграла:
то Е можно вынести за знак интеграла: , или
, или  (2.19)
(2.19) , получим
, получим (2.20)
(2.20) – площадь гауссовой поверхности. Тогда
– площадь гауссовой поверхности. Тогда . (2.21)
. (2.21) . Тогда
. Тогда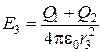 . (2.22)
. (2.22) это выражение можно переписать в виде:
это выражение можно переписать в виде: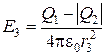 . (2.23)
. (2.23) . (2.24)
. (2.24) м / Ф) и произведем вычисления:
м / Ф) и произведем вычисления: изменяется по закону
изменяется по закону 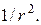 В точке
В точке  напряженность
напряженность  В точке
В точке  (r стремится к
(r стремится к  слева)
слева)  . В области
. В области 
 изменяется по закону
изменяется по закону  , причем в точке
, причем в точке  . Таким образом, функция E (r) в точках
. Таким образом, функция E (r) в точках 











