
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность электростатического поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Принцип суперпозиции. Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства – создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный» заряд испытывает действие силы. Опыт показывает, что сила может быть представлена, как F=q’E, Где вектор E называют напряженностью электрического поля в данной точке. E можно определить как силу, действующую на единичный положительный неподвижный заряд. Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, который создавали бы каждый из зарядов в отдельности.
Поток вектора напряженности электрического поля. По определению потоком векторного поля
Тогда поток через всю поверхность S будет:
Заметим, что поток – величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении ФЕ. Изменение направления нормали на противоположное изменит знак En, а значит и знак потока ФЕ. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Численно поток равен количеству силовых линий, пресекающих данную поверхность.Размерность потока в СИ: [ФЕ] = В·м (отметим, что она совпадает с размерностью величины q/εо). 3. Теорема Гаусса в интегральной и дифференциальной формах в вакууме и ее применение для расчета электрических полей Теорема Гаусса Поток вектора напряжённости электрического поля через любую, произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности электрических зарядов, делённой на электрическую постоянная ε0:
Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом:
где ρ — объёмная плотность заряда
Работа электростатического поля при перемещении зарядов. Циркуляция вектора напряженности. Работа электростатического поля (A)
A = Fd=qEd,
A1 = Fd1 cos , но d1 cos = d, A1 = qEd A = A1 A1,2,3,1 = A1,2 + A2,3 + A3,1
A1,2,3,1 = qEd1 cos a + Eqh cos 90° + Eqd cos 180° = qEd + 0 + (- qEd) A1,2,3,1 =0 т. е. работа при перемещении заряда между двумя точками в электростатическом поле не зависит от формы траектории, а зависит от положения этих точек. Работа по замкнутой траектории равна нулю.
Из принципа суперпозиции следует, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0: Для любого контура в электростатическом поле циркуляция напряженности – тождественный нуль. Напряженность электростатического поля (с точностью до знака) может быть истолкована как градиент некоторой функции координат, называемой потенциалом электростатического поля Связь напряженности и потенциала. Работа сил поля
Модуль напряженности в любой точке поля численно равен разности потенциалов, приходящейся на единицу длины линии напряженности. Чем меньше Δl, тем теснее расположены эквипотенциальные поверхности, тем больше в этом месте напряженность поля. В однородном поле Δl может быть любое. Если Δl = d, то
Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м). Уравнение Пуассона. Проблема расчета электростатического поля в общем случае не является безнадежной. Действительно, если вспомнить выражение векторного поля через потенциал электростатического поля То есть Подставив (1.65) в
|
||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 697; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.190.93 (0.007 с.) |


 через площадку
через площадку  называется величина (рис.2.1)
называется величина (рис.2.1)
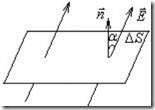 Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской то определение потока нужно применить кбесконечно малому элементу поверхности, а именно записать:
Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской то определение потока нужно применить кбесконечно малому элементу поверхности, а именно записать:


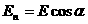 .
. .
. ,
,
 .
.
 .
. :
: .
. Если расстояние Δl между поверхностями по нормали мало, то на этом участке поле можно считать однородным. Поэтому можно воспользоваться формулой для расчета работы по перемещению заряда q0 в однородном электростатическом поле:
Если расстояние Δl между поверхностями по нормали мало, то на этом участке поле можно считать однородным. Поэтому можно воспользоваться формулой для расчета работы по перемещению заряда q0 в однородном электростатическом поле: 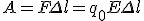 . Приравнивая два выражения для работы, получим:
. Приравнивая два выражения для работы, получим:
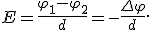
 (1.65)
(1.65) 
 получаем:
получаем: Уравнение Пуассона.
Уравнение Пуассона.


