
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.4. Циркуляция вектора напряженностиСодержание книги
Поиск на нашем сайте
Электростатического поля. Потенциал поля
Если в электростатическом поле точечного заряда
Так как Работа при перемещении заряда
Из формулы (1.10) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, то есть
Если в качестве заряда, переносимого
Этот интеграл называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (1.12), является потенциальным. Из обращения в нуль циркуляции вектора Формула (1.12) справедлива только для электростатического поля; для электрического поля движущихся зарядов циркуляция вектора напряжен Тело, находящееся в потенциальном поле сил, в частности, в электростатическом поле, обладает потенциальной энергией, за счет которой силами поля совершается работа. Поэтому работу кулоновских сил (формула (1.10)) можно представить как разность потенциальных энергий, которыми обладает точечный заряд
Таким образом, потенциальная энергия заряда
где С – постоянная интегрирования, которая определяется из граничных
Если поле создается системой из n точечных зарядов
Из формул (1.14) и (1.15) можно выделить отношение
Таким образом, потенциал в какой-либо точке электростатического поля есть физическая скалярная величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формулы (1.16) с учетом (1.14) следует, что потенциал точки поля где r – расстояние от заряда до заданной точки. Работа, совершаемая силами электростатического поля по перемещению заряда то есть работа кулоновских сил численно равна произведению величины Если перемещать заряд
Таким образом, потенциал – это физическая величина, определяемая работой по перемещению единичного положительного заряда из данной точки поля в бесконечность. Единица потенциала – вольт (В): 1 В – это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж (см. формулу (1.16)): Из формул (1.15) и (1.16) вытекает, что если электростатическое поле создается несколькими зарядами, то потенциал точки поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.67.105 (0.007 с.) |

 из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд
из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд  (рис. 1.8), то кулоновская сила
(рис. 1.8), то кулоновская сила  , приложенная к заряду, совершает работу. Работа, совершаемая силой
, приложенная к заряду, совершает работу. Работа, совершаемая силой  равна
равна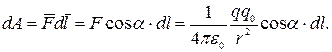
 то
то 
 (1.10)
(1.10)
 то есть не зависит от траектории перемещения заряда, а определяется только
то есть не зависит от траектории перемещения заряда, а определяется только  (1.11)
(1.11) где
где  проекция вектора
проекция вектора 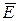 на направление элементарного перемещения. Тогда формулу (1.11) можно записать в виде
на направление элементарного перемещения. Тогда формулу (1.11) можно записать в виде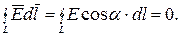 (1.12)
(1.12) (1.13)
(1.13)
 потенциальная энергия
потенциальная энергия  и
и  . Следовательно, потенциальная энергия заряда
. Следовательно, потенциальная энергия заряда 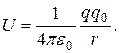 (1.14)
(1.14) то
то 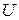 заряда
заряда  в полях, создаваемых каждым из зарядов в отдельности:
в полях, создаваемых каждым из зарядов в отдельности: (1.15)
(1.15) , которое называется потенциалом и является энергетической характеристикой
, которое называется потенциалом и является энергетической характеристикой  (1.16)
(1.16)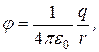 (1.17)
(1.17)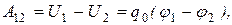 (1.18)
(1.18) откуда
откуда (1.19)
(1.19)




