
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.6. Плоская электромагнитная волнаСодержание книги
Поиск на нашем сайте
Перед исследованием плоской электромагнитной волны запишем проекции уравнений (6.29) и (6.31) на координатные оси. Тогда, приняв во внимание формулы (6.36), получим вместо каждого из векторных уравнений три
Уравнения (6.30) и (6.32) можно записать в скалярном виде, использовав соотношение (6.37):
Пусть плоская электромагнитная волна распространяется в однородной непроводящей среде ( Поэтому уравнения (6.51) – (6.54) упрощаются следующим образом:
Первое из уравнений (6.56) и уравнение (6.58) показывают, что составляющая Вторые и третьи уравнения (6.55) и (6.56) можно объединить в две группы следующим образом:
Первая группа уравнений связывает составляющие Возьмем для описания волны систему уравнений (6.59), положив
Подставив затем
Продифференцировав по х второе уравнение (6.59), после аналогичных преобразований получим волновое уравнение для составляющей
Уравнения (6.61) и (6.62) представляют собой частный случай уравнений (6.47) и (6.48). Решением уравнения (6.61) является гармоническая функция
Решение уравнения (6.62) имеет аналогичный вид
Подставим функции (6.63) и (6.64) в систему (6.59)
Для того чтобы эти равенства выполнялись, необходимы следующие условия:
Таким образом, в электромагнитной волне колебания векторов
Умножив уравнение (6.63) на орт оси у, а уравнение (6.64) на орт оси z, получим уравнения плоской электромагнитной волны в векторной форме:
На рис. 6.21 показан «моментальный снимок» плоской электромагнитной волны. Из него видно, что векторы  и и  образуют с направлением образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы напряженности электрического и магнитного полей изменяются со временем по гармоническому закону.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.250.115 (0.007 с.) |

 (6.51)
(6.51) (6.52)
(6.52) ; (6.53)
; (6.53) (6.54)
(6.54)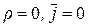 ). Направим ось х перпендикулярно к волновым поверхностям. Тогда
). Направим ось х перпендикулярно к волновым поверхностям. Тогда  (6.55)
(6.55) (6.56)
(6.56) (6.57)
(6.57) (6.58)
(6.58) не может зависеть ни от t, ни от х. Первое из уравнений (6.55)
не может зависеть ни от t, ни от х. Первое из уравнений (6.55) .
.  (6.59)
(6.59) (6.60)
(6.60) и
и  , вторая – составляющие
, вторая – составляющие  и
и  . Предположим, что первоначально было создано переменное электрическое поле
. Предположим, что первоначально было создано переменное электрическое поле 
 из второго уравнения, получим волновое уравнение для составляющей
из второго уравнения, получим волновое уравнение для составляющей  (6.61)
(6.61) (6.62)
(6.62)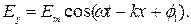 (6.63)
(6.63) (6.64)
(6.64)

 (6.65)
(6.65) (6.66)
(6.66)



