
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.3. Резонанс в электрических цепяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Резонансом в электрической цепи называется режим участка, содержащего индуктивный и емкостный элементы, при котором угол Различают несколько видов резонанса: резонанс напряжений (при Резонанс напряжений. Из выражения (6.10) следует, что при последовательном соединении
и
где Q – добротность контура. Так как добротность колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе превышает напряжение U, приложенное к цепи. Из выражения (6.16) следует, что добротность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине
Резонанс токов возможен в цепи с параллельным соединением ветвей Разложим вектор тока
Так как
то, подставляя эти выражения в (6.17), получим
где g и b – активная и реактивная проводимости цепи. Найдем соотношение между активной g, реактивной b и полной Y проводимостью цепи. Из векторной диаграммы следует, что модуль действующего значения тока в неразветвленной части цепи равен
Так как полная проводимость Y равна обратной величине полного
В режиме резонанса
где Тогда условие (6.22) примет вид
где Из (6.23) после преобразования имеем
где Анализ выражения (6.24) позволяет сделать ряд выводов: 1. Резонансная частота 2. Резонанс токов возможен, если сопротивления 3. При Рассмотрим контур с малыми омическими потерями в режиме резонанса токов. 1. Так как
2. Ток в неразветвленной части цепи
минимальный, что позволяет по показаниям амперметра обнаруживать
3. Активные и реактивные составляющие токов
Так как
Векторная диаграмма цепи при резонансе токов приведена на рис. 6.18. Ток в общей части цепи равен активной составляющей тока
Если
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

 сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.
сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.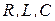 ток в цепи приобретает максимальное значение при
ток в цепи приобретает максимальное значение при 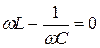 , то есть при
, то есть при 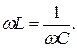 Этому условию удовлетворяет частота
Этому условию удовлетворяет частота (6.15)
(6.15) В этом случае
В этом случае  , Z = R → min, падения напря-жения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе (рис. 6.15). Таким образом, при резонансе напря-жений
, Z = R → min, падения напря-жения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе (рис. 6.15). Таким образом, при резонансе напря-жений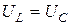 ,
,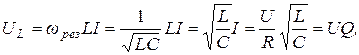 (6.16)
(6.16)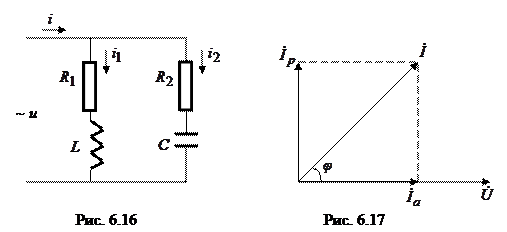 Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.
Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.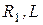 и
и 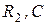 (рис. 6.16). Между током в неразветвленной части цепи и напряжением имеется некоторый сдвиг фаз
(рис. 6.16). Между током в неразветвленной части цепи и напряжением имеется некоторый сдвиг фаз 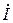 на две составляющие: активную
на две составляющие: активную  , находящуюся в фазе с вектором напряжения
, находящуюся в фазе с вектором напряжения  на зажимах цепи, и реактивную
на зажимах цепи, и реактивную  , перпендикулярную к
, перпендикулярную к 
 (6.17)
(6.17)
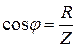 и
и 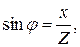
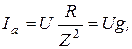 (6.18)
(6.18)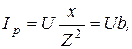 (6.19)
(6.19) (6.20)
(6.20)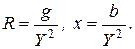 (6.21)
(6.21)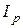 , а, следовательно, и реактивная проводимость b цепи должны равняться
, а, следовательно, и реактивная проводимость b цепи должны равняться 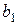 и
и 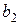 параллельных ветвей. При
параллельных ветвей. При  (6.22)
(6.22)
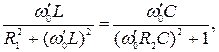 (6.23)
(6.23)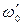 – циклическая частота резонанса токов.
– циклическая частота резонанса токов. (6.24)
(6.24)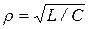 – характеристическое сопротивление контура.
– характеристическое сопротивление контура. и
и 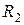 .
. , или меньше
, или меньше 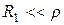 и
и  , что справедливо для многих цепей,
, что справедливо для многих цепей, 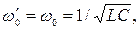 то есть резонансная частота при резонансе токов равна
то есть резонансная частота при резонансе токов равна  и общее сопротивление контура активное, то полная проводимость контура равна активной проводимости и минимальна:
и общее сопротивление контура активное, то полная проводимость контура равна активной проводимости и минимальна: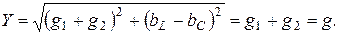

 , параметров L или C.
, параметров L или C.
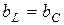 , то реактивные составляющие токов при резонансе равны
, то реактивные составляющие токов при резонансе равны 

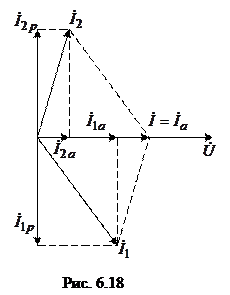 Токи в ветвях
Токи в ветвях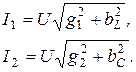
 то есть
то есть 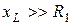
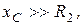 то
то 
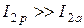
 то есть токи в ветвях значительно превышают по величине ток в неразветвленной части цепи. Это свойство – усиление тока – является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и название этого явления.
то есть токи в ветвях значительно превышают по величине ток в неразветвленной части цепи. Это свойство – усиление тока – является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и название этого явления.


