
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.7. Энергия и импульс электромагнитной волныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для характеристики переноса энергии любой волной в физике введена векторная величина, называемая плотностью потока энергии
Плотность энергии
В непроводящей среде для данной точки пространства векторы
или
Умножив плотность энергии электромагнитной волны на ее фазовую скорость [формула (6.49)], получим плотность потока энергии
Векторы
Вектор Найдем выражение для интенсивности распространяющейся электромагнитной волны. Мгновенные значения напряженностей электрического
На практике обычно имеют дело не с мгновенным, а со средним значением энергии по времени
Таким образом, интенсивность I или средняя энергия, проходящая Если электромагнитные волны поглощаются или отражаются веществом (а это подтверждается опытами Г. Герца), то из теории Максвелла следует, что они должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны
Направление этой силы совпадает с направлением распространения Согласно теории Максвелла в случае, когда тело полностью поглощает падающую на него энергию, давление равно среднему (по времени) значению плотности энергии падающей волны:

Если тело отражает волну, посылая в обратном направлении волну
где ω ср. – среднее значение плотности энергии падающей волны. Для идеально отражающего тела k = 1 и р = 2 ω ср.. Из того факта, что электромагнитная волна оказывает давление на
Наличие импульса позволяет приписать электромагнитному полю массу, связанную с импульсом соотношением
Выражение
Полученное соотношение является частным случаем вытекающего из специальной теории относительности универсального закона взаимосвязи между массой и энергией
В 1899 г. П.Н. Лебедев экспериментально доказал существование давления света на твердые тела, а в 1910 г. – на газы. Опыты Лебедева имели Таким образом, существование электромагнитных волн и их свойства, определяемые теорией Максвелла, были полностью подтверждены опытами Герца, Лебедева и выводами специальной теории относительности.
Краткие выводы · Электромагнитными колебаниями называют периодические процессы, при которых происходят взаимосвязанные изменения электрических · Идеальный колебательный контур (
где
· Период свободных гармонических колебаний в идеальном колебательном контуре (формула Томсона)
· В реальном колебательном контуре из-за наличия омического сопротивления свободные колебания со временем будут затухать. Дифферен-циальное уравнение свободных затухающих колебаний линейной системы
где · Колебания, возникающие под действием внешнего периодически
где
· Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешнего переменного фактора к собственной частоте системы называют резонансом. Резонансная циклическая частота и резонансная амплитуда
· Установившиеся вынужденные электромагнитные колебания в цепи, содержащей резистор, катушку индуктивности и конденсатор, называют · Закон Ома для действующих значений силы тока и напряжения в цепи переменного тока, содержащей последовательно соединенные резистор, индуктивный и емкостный элементы, имеет вид
где Z – полное сопротивление цепи. Разность фаз между напряжением и силой тока, определяемая из векторной диаграммы цепи,
· Явление резкого возрастания напряжения на катушке индуктивности и конденсаторе контура из последовательно соединенных элементов
то есть добротность контура определяет, во сколько раз напряжение на · Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно соединенные элементы · Академик АН СССР Л.И. Мандельштам (1879-1944) отмечал: «Теория колебаний объединяет, обобщает различные области физики... Каждая из областей физики – оптика, механика, акустика – говорит на своем „национальном“ языке. Но есть „интернациональный“ язык, и это – язык теории колебаний…Изучая одну область, вы получите тем самым интуицию и знания совсем в другой области». В этом высказывании обоснована полезность аналогии между механическими и электромагнитными колебаниями. Знание такой аналогии (табл. 6.2) позволяет решать ряд задач механики и электродинамики. · Электромагнитная волна – это переменное электромагнитное · Существование электромагнитных волн вытекает из уравнений
Таблица 6.2
· Источником электромагнитной волны может быть колебательный контур или проводник, по которому протекает быстропеременный электрический ток. · Из уравнений Максвелла следует, что векторы
где · Фазовая скорость электромагнитных волн определяется
В вакууме ( · Электромагнитные волны являются поперечными волнами –
· Плоская электромагнитная волна, распространяющаяся вдоль оси х, описывается волновыми уравнениями
где индексы y и z лишь подчеркивают, что векторы
· Перенос энергии электромагнитной волной характеризуется
Вектор
где
· Интенсивность электромагнитной волны I пропорциональна
· Одним из выводов теории Максвелла является наличие давления электромагнитных волн на тела. Существование такого давления приводит к выводу о наличии у поля электромагнитной волны импульса
где W – энергия электромагнитного поля.
Вопросы для самоконтроля и повторения 1. Какой процесс называется колебательным? Какие колебания назы-ваются свободными, гармоническими, вынужденными? 2. Выведите дифференциальное уравнение свободных электромагнитных колебаний в контуре. По какой формуле определяется период колебаний в контуре с малыми омическими потерями? 3. Какие колебания называются затухающим? Запишите дифференциальное уравнение затухающих колебаний в RLC -контуре и его решение. 4. Какие колебания называются вынужденными? Запишите дифференциальное уравнение вынужденных колебаний в электрическом контуре 5. Что называется резонансом? Запишите выражения для циклической частоты и амплитуды колебаний при резонансе. 6. Что называется переменным электрическим током? Выведите закон Ома для цепи переменного тока. От чего зависят индуктивное и емкостное сопротивления? 7. Каковы характерные признаки резонанса напряжений, резонанса 8. Что представляет собой электромагнитная волна? Что может служить источником электромагнитных волн? 9. От чего зависит скорость распространения электромагнитной волны? 10. На какие виды делятся электромагнитные волны? Каковы источники излучения разных видов волн? 11. Расположите в порядке убывания длины электромагнитных волн, используемых в различных устройствах: а) инфракрасное излучение пульта дистанционного управления; б) рентгеновское излучение; в) электромагнитное излучение мобильного телефона; г) излучение радиостанции, 12. Какими свойствами обладают электромагнитные волны? 13. Запишите волновые уравнения для векторов 14. Как определяется объемная плотность энергии в электромагнитной волне? 15. Каков физический смысл вектора Умова-Пойнтинга? Как опреде-ляется направление и модуль вектора плотности потока энергии?
Примеры решения задач Задача 1. Колебательный контур содержит катушку индуктивностью
Дано: Найти: Решение
Коэффициент затухания колебаний
Период колебаний и логарифмический декремент затухания
Добротность колебательного контура
Ответ:
Дано: Найти: Решение
Ответ: Задача 3. Длина электромагнитной волны в вакууме, на которую настроен колебательный контур, равна 12 м. Пренебрегая омическим сопротивлением контура, определить максимальный заряд Дано: Найти: Решение Длина электромагнитной волны в вакууме
откуда
При
где
Ответ: Задача 4. В вакууме вдоль оси х распространяется плоская электромагнитная волна и падает по нормали на поверхность тела, полностью ее Дано: Найти: p. Решение Согласно теории Максвелла, давление электромагнитной волны на тело
где k – коэффициент отражения,
где
Учитывая, что
или
Тогда
Ответ:
Задачи для самостоятельного решения
2. Колебательный контур состоит из катушки индуктивностью 80мкГн, конденсатора емкостью 100 пФ и резистора сопротивлением 0,5Ом. Какую мощность необходимо подводить к контуру, чтобы в нем поддерживались незатухающие гармонические колебания, при которых амплитуда напряжения на конденсаторе равна 4В? (Ответ: Р = 5мкВт). 3. Частота затухающих электромагнитных колебаний в контуре с добротностью Q = 2500 равна 550 кГц. Определить время, за которое амплитуда силы тока в контуре уменьшится в 4 раза. (Ответ: t = 2мс). 4. Определить минимальное сопротивление колебательного контура
6. В цепь переменного тока с частотой (Ответ: С = 29,8мкФ, I = 3,32А).
8. Электромагнитная волна с частотой 4МГц переходит из немагнитной среды с диэлектрической проницаемостью 9. Катушка, индуктивность которой
10. Определить длину электромагнитной волны в вакууме, на которую настроен колебательный контур, если максимальный заряд на обкладках конденсатора 11. В вакууме вдоль оси х распространяется плоская электромагнитная волна и падает по нормали на вещество с коэффициентом отражения k= 0. Амплитуда напряженности магнитного поля волны равна 0,15А/м. Определить давление, оказываемое волной на вещество. (Ответ: р= 14,1нПа). 12. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны составляет 18,8В/м. Определить интенсивность волны. (Ответ: I= 0,47Вт/м2). VII. ОСНОВЫ ВОЛНОВОЙ ОПТИКИ
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.047 с.) |

 . Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором
. Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором  на скорость волны
на скорость волны

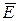 и
и  изменяются в одинаковой фазе, поэтому соотношение (6.65) справедливо
изменяются в одинаковой фазе, поэтому соотношение (6.65) справедливо 
 (6.67)
(6.67)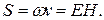 (6.68)
(6.68) совпадает с направлением переноса энергии, а модуль этого вектора определяется соотношением (6.68). Следовательно, вектор плотности потока энергии электромагнитной волны можно представить как векторное произведение
совпадает с направлением переноса энергии, а модуль этого вектора определяется соотношением (6.68). Следовательно, вектор плотности потока энергии электромагнитной волны можно представить как векторное произведение (6.69)
(6.69)
 . Используя соотношение (6.65) и учитывая, что среднее значение квадрата гармонической функции равно 1/2 и в вакууме
. Используя соотношение (6.65) и учитывая, что среднее значение квадрата гармонической функции равно 1/2 и в вакууме  , получим
, получим (6.70)
(6.70) ). При этом они подвергаются со стороны магнитного поля волны действию силы Лоренца, величину которой в расчете на единицу объема тела можно найти по формуле
). При этом они подвергаются со стороны магнитного поля волны действию силы Лоренца, величину которой в расчете на единицу объема тела можно найти по формуле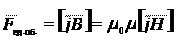
 (
( – интенсивность, то есть плотность потока энергии падающей волны, k – коэффициент отражения), то давление равно
– интенсивность, то есть плотность потока энергии падающей волны, k – коэффициент отражения), то давление равно

 . Разделив модуль выражения (6.71) на скорость света с, получим массу единицы объема электромагнитного поля:
. Разделив модуль выражения (6.71) на скорость света с, получим массу единицы объема электромагнитного поля:
 представляет собой плотность энергии поля
представляет собой плотность энергии поля 

 ) является примером гармонического осциллятора – системы, процессы в которой описываются дифференциальным уравнением
) является примером гармонического осциллятора – системы, процессы в которой описываются дифференциальным уравнением
 – собственная циклическая частота колебаний. В идеальном контуре свободные колебания будут незатухающими, и заряд на конден-саторе изменяется со временем по закону синуса или косинуса:
– собственная циклическая частота колебаний. В идеальном контуре свободные колебания будут незатухающими, и заряд на конден-саторе изменяется со временем по закону синуса или косинуса:


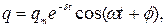
 – коэффициент затухания;
– коэффициент затухания;  – циклическая частота затухающих колебаний;
– циклическая частота затухающих колебаний;  – амплитуда затухающих колебаний.
– амплитуда затухающих колебаний.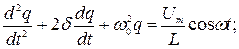





 ,
,
 при совпадении частоты ω внешнего переменного напряжения с собственной частотой
при совпадении частоты ω внешнего переменного напряжения с собственной частотой 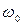 колебательного контура, называют резонансом напряжений
колебательного контура, называют резонансом напряжений 
 при приближении
при приближении 


















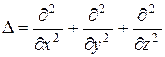 – оператор Лапласа, v – фазовая скорость волны. Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля могут действительно
– оператор Лапласа, v – фазовая скорость волны. Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля могут действительно 
 , поэтому скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
, поэтому скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме. образуют правовинтовую систему. Из уравнений Максвелла также следует, что в электромагнитной волне
образуют правовинтовую систему. Из уравнений Максвелла также следует, что в электромагнитной волне 




 направлен в сторону распространения электромагнитной волны, а его модуль равен произведению плотности энергии
направлен в сторону распространения электромагнитной волны, а его модуль равен произведению плотности энергии  на скорость распространения волны в среде
на скорость распространения волны в среде



 .
. ;
; 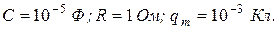

 где
где 






 Задача 2. Показания амперметров, включенных в ветви с конденсатором, катушкой индуктивности и резистором, соответственно равны 2А, 3А и 1А (рис. 6.22). Что покажет амперметр в неразветвленной части цепи?
Задача 2. Показания амперметров, включенных в ветви с конденсатором, катушкой индуктивности и резистором, соответственно равны 2А, 3А и 1А (рис. 6.22). Что покажет амперметр в неразветвленной части цепи?

 Построим векторную диаграмму цепи с учетом фазовых соотношений между напряжением и током на отдельных элементах (рис. 6.23), где
Построим векторную диаграмму цепи с учетом фазовых соотношений между напряжением и током на отдельных элементах (рис. 6.23), где  – реактивная составляющая силы тока. Тогда модуль действующего значения силы тока в неразветвленной части цепи (искомое показание амперметра) равен
– реактивная составляющая силы тока. Тогда модуль действующего значения силы тока в неразветвленной части цепи (искомое показание амперметра) равен

 .
.



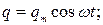





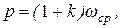
 – среднее значение плотности энергии падающей волны. Для рассматриваемого случая
– среднее значение плотности энергии падающей волны. Для рассматриваемого случая

 , имеем
, имеем




 1. Колебательный контур через ключ К подключен к источнику ЭДС с некоторым внутренним сопротивлением r (рис. 6.24). Первоначально ключ
1. Колебательный контур через ключ К подключен к источнику ЭДС с некоторым внутренним сопротивлением r (рис. 6.24). Первоначально ключ  ,
,  ).
). 5. В цепи переменного тока (рис. 6.25) действующие значения напряжения
5. В цепи переменного тока (рис. 6.25) действующие значения напряжения 
 . Определить действующее значение напряжения
. Определить действующее значение напряжения  .(Ответ: UAB = 18 B).
.(Ответ: UAB = 18 B).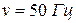 и действующим значением напряжения U = 300B последовательно включены конденсатор, резистор сопротивлением R = 50Ом и катушка индуктивностью L = 0,1Гн (рис. 6.26). Падения напряжения
и действующим значением напряжения U = 300B последовательно включены конденсатор, резистор сопротивлением R = 50Ом и катушка индуктивностью L = 0,1Гн (рис. 6.26). Падения напряжения  Определить: 1) емкость конденсатора; 2) действующее значение силы тока.
Определить: 1) емкость конденсатора; 2) действующее значение силы тока. 7. Генератор, частота которого 32 кГц и амплитудное значение напряжения 120 В, включен в резонирующую цепь, емкость которой 1нФ. Определить амплитудное значение напряжения на конден-саторе, если омическое сопротивление цепи 5Ом. (Ответ: 119кВ).
7. Генератор, частота которого 32 кГц и амплитудное значение напряжения 120 В, включен в резонирующую цепь, емкость которой 1нФ. Определить амплитудное значение напряжения на конден-саторе, если омическое сопротивление цепи 5Ом. (Ответ: 119кВ). в вакуум. Определить
в вакуум. Определить  ).
). , присоединена к плоскому конденсатору с площадью пластин 100см2 и расстоянием между ними
, присоединена к плоскому конденсатору с площадью пластин 100см2 и расстоянием между ними  ).
). , а максимальная сила тока в контуре
, а максимальная сила тока в контуре  . Активным сопротивлением контура пренебречь. (Ответ:
. Активным сопротивлением контура пренебречь. (Ответ:  ).
).


