
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механические и электромагнитные колебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте · Уравнение гармонических колебаний
где х – смещение колеблющейся величины от положения равновесия; А – амплитуда колебаний; ω = 2π/ T = 2πn – круговая (циклическая) частота; n = 1/ T – частота, Т – период колебаний; φ – начальная фаза. · Скорость и ускорение материальной точки, совершающей гармонические колебания:
Кинетическая энергия колеблющейся точки массой m
Потенциальная энергия
Полная энергия
Период колебаний пружинного маятника
где m – масса пружинного маятника, k – жесткость пружины. Период колебаний физического маятника
где I – момент инерции маятника относительно оси колебаний, l – расстояние между точкой подвеса и центром масс маятника. Период колебаний математического маятника длиной l
· Сложение гармонических колебаний одного направления и одинаковой частоты: а) амплитуда результирующего колебания
б) начальная фаза результирующего колебания
· Уравнение траектории движения точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты
· Уравнение затухающих колебаний
где · Логарифмический декремент затухания
где A (t) и A (t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, τ=1/β – время релаксации, Nе – число колебаний, совершаемых за время уменьшения амплитуды в е раз. · Добротность колебательной системы
· Амплитуда вынужденных колебаний и резонансная частота
· Период собственных колебаний электрического колебательного контура, сопротивление которого R = 0, индуктивность L, емкость C (формула Томсона)
· Полная энергия колебательного контура
· Частота затухающих электромагнитных колебаний
Упругие и электромагнитные волны · Уравнение упругой плоской волны, распространяющейся вдоль оси Ох
где ξ - смещение любой из точек среды с координатой х в момент t; v – фазовая скорость распространения колебаний в среде, k = 2π/λ = ω/v– волновое число λ = v T – длина волны. · Связь разности фаз ∆φ колебаний с расстоянием ∆ x между точками среды, отсчитанным в направлении распространения колебаний;
· Скорость и длина электромагнитных волн в веществе
где c, λ0 – скорость и длина электромагнитных волн в вакууме, · Уравнение плоской монохроматической электромагнитной волны, распространяющейся вдоль оси Ох, E = E mcos(ω t – kx); H = H mcos(ω t – kx). · Связь между модулями векторов Е и Н в бегущей волне
· Интенсивность плоской бегущей электромагнитной волны
Примеры решения задач Пример 4.1. Материальная точка массой m = 5 г совершает гармонические колебания с частотой ν = 0,5 Гц. Амплитуда колебаний A = 3 см. Определить: 1) скорость v точки в момент времени, когда смещение х = 1,5 см; 2) максимальную силу Fmах , действующую на точку; 3) полную энергию Е колеблющейся точки. Решение. 1. Уравнение гармонического колебания имеет вид
а формулу скорости получим, взяв первую производную по времени от смещения:
Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого выразим из уравнений (1) и (2):
Учитывая, что
Решив последнее уравнение относительно v, найдем
Выполнив вычисления по этой формуле, получим v = ± 8,2 см/с. Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус – когда направление скорости совпадает с отрицательным направлением оси х. 2. Силу, действующую на материальную точку, найдем по второму закону Ньютона:
где а – ускорение точки, которое получим, взяв производную по времени от скорости:
или
Подставив выражение ускорения в формулу (3), получим
Сила максимальна, когда
Подставив в это уравнение значения величин π, ν, m и А, найдем F mах = 1,49 мН. 3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия Е колеблющейся точки равна максимальной кинетической энергии Т mах:
Максимальную скорость определим из формулы (2), положив
Подставив выражение скорости в формулу (4), найдем
Произведя вычисления, получим
Пример 4.2. Физический маятник представляет собой тонкий однородный стержень. Определить длину стержня l, если частота колебаний маятника максимальна, когда точка подвеса О находится от центра масс С на расстоянии а = 20,2 см. Решение. Циклическая частота колебаний физического маятника
где m – масса маятника, I – момент его инерции, a – расстояние от центра масс до точки подвеса. Согласно теореме Штейнера момент инерции стержня относительно точки подвеса, отстоящей от центра масс на расстоянии а?
Подставив (2) в (1), получим
Найдем экстремум функции (3)
откуда l 2 – 12 а 2 = 0, т.е. искомая длина маятника l = Пример 4.3. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений. Для этого воспользуемся формулой
В данном случае
Так как по условию
Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений в условии задачи следует, что смещение точки по осям координат ограничено и заключено в пределах от –1 до +1 см по оси Ох и от –2 до +2 см по оси Оу. Для построения траектории найдем по уравнению (1) значения у, соответствующие ряду значений х, удовлетворяющих условию │ х │≤ 1 см, и составим таблицу:
Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t = 0 координаты точки равны х (0) = 1 см и у (0) = 2 см. В последующий момент времени, например при t 1= 1 c, координаты точек изменятся и станут равными х (1) = –1 см, у (t) = 0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указатьнаправление движения точки по траектории. На рисунке это направление движения указано стрелкой (от точки А к началу координат). После того, как в момент t 2 = 2c колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении.
Решение. Напряжение на конденсаторе изменяется по гармоническому закону
где
Отсюда находим
Период собственных колебаний в контуре определяется по формуле Томсона Определим индуктивность Полная энергия контура равна сумме энергий электрического и магнитного полей
и равна либо максимальной энергии поля конденсатора либо максимальной энергии катушки индуктивности
Зная полную энергию, можно определить максимальную силу протекающего по катушке индуктивности тока:
Пример 4.5. Тело совершает колебания с частотой n = 50 Гц. Логарифмический декремент затухания λ равен 0,01. Определить: 1) время, за которое амплитуда колебаний тела уменьшится в 20 раз; 2) число полных колебаний тела, чтобы произошло подобное уменьшение амплитуды. Решение. Амплитуда затухающих колебаний
где А 0 – амплитуда колебаний в момент t = 0, β – коэффициент затухания. Логарифмический декремент затухания λ = b Т (Т = 1/n– условный период затухающих колебаний). Тогда β = λn и выражение (1) можно записать в виде
откуда искомое время
Число искомых полных колебаний N = t / T = t n. Вычислив, получим 1) t = 6с; 2) N = 300. Пример 4.6. Колебательный контур состоит из катушки индуктивностью L = 25 мГн, конденсатора емкостью С = 10 мкФ и резистора. Определить сопротивление резистора, если известно, что амплитуда тока в контуре уменьшилась в е раз за 16 полных колебаний. Решение. Число колебаний, совершаемых за время уменьшения амплитуды силы тока в е раз N e = τ/ T, где τ = 1/b – время релаксации, T = 2π / Подставляя эти выражения в (1), получим
Отсюда искомое сопротивление:
Вычисляя, получим R = 0,995 Ом. Пример 4.7. Плоская волна распространяется вдоль прямой со скоростью v = 20 м/с. Две точки, находящиеся на этой прямой на расстояниях x1 =12 м и х2 = 15 м от источника волн, колеблются с разностью фаз ∆ φ = 0,75 π. Определить длину волны l, написать уравнение волны и найти смещение указанных точек в момент t = 1,2 c, если амплитуда колебаний А = 0,1 м. Решение. Точки, находящиеся друг от друга на расстоянии, равном длине волны l, колеблются с разностью фаз, равной 2π; точки, находящиеся друг от друга на любом расстоянии ∆ х, колеблются с разностью фаз, равной
Решая это равенство относительно l, получаем
Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия, получим
Для того чтобы написать уравнение плоской волны, надо определить циклическую частоту ω. Так как Произведем вычисления: Зная амплитуду А колебаний, циклическую частоту ω и скорость v распространения волны, можно написать уравнение плоской волны для данного случая:
где A =0,1 м, ω= 5π с-1, v =20 м/с. Чтобы найти смещение x указанных точек, достаточно в уравнение (2) подставить значения t и х:
Пример 4.8. Определить энергию, переносимую плоской синусоидальной электромагнитной волной, распространяющейся в вакууме, за t = 1 с через поверхность площадью Sпл = 1м2, расположенную перпендикулярно направлению распространения волны. Амплитуда напряженности электрического поля волны Е0 = 5 мВ/м. Период волны Т<<t. Решение. Плотность потока энергии (или интенсивность излучения) электромагнитных волн, т. е. количество энергии, переносимой за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, определяется вектором Пойнтинга
где Учитывая, что S = EH.. Так как величины
Таким образом, величина S является функцией времени. Согласно определению плотности потока энергии, имеем
где Из выражений (2) и (1) получим выражение для энергии, переносимой за бесконечно малый промежуток времени dt:
Для определения dW необходимо знать величину H 0, которая может быть найдена из соотношения
Отсюда
По условию,
Подставляя (4) в (3), получим
Энергию, переносимую волной за время t, найдем интегрированием полученного выражения
По условию задачи T << t, или 2π/w << t, 2π << w t. При очень больших значениях w t вторым слагаемым в скобке можно пренебречь – значения синуса при любом аргументе не превосходят единицу, а в знаменателе стоит очень большая величина. Тогда
Подставляя числовые значения, получим
КОНТРОЛЬНАЯ РАБОТА №4
ВАРИАНТ 1
1. Амплитуда гармонических колебаний точки А = 5 см, амплитуда скорости vmax = 7,85 см/c. Вычислить циклическую частоту ω колебаний и максимальное ускорение a max точки. 2. Точка совершает одновременно два гармонических колебания одинаковой частоты, которые происходят во взаимно перпендикулярных направлениях. Уравнения колебаний х = А cos ω t и y = А cos (ω t + φ). Определить уравнение траектории точки. Принять A = 2 см, φ = π/2. 3. Материальная точка, масса которой m = 10 г, осуществляет гармонические колебания по закону косинуса с периодом Т = 2 си начальной фазой φ = 0. Полная механическая энергия точки Е = 0,1 мДж. Определить амплитуду колебаний А и записать закон движения точки. Вычислить максимальное значение F max силы, которая действует на точку. 4. Груз массой m = 500 г, подвешенный к спиральной пружине жесткостью k = 20 Н/м, совершает упругие колебания в некоторой среде. Логарифмический декремент затухания колебаний l = 0,004. Определить количество N полных колебаний, которые может совершить груз, чтобы энергия колебаний уменьшилась в п = 2 раза. За какое время D t состоится это уменьшение? 5. Плоская гармоническая звуковая волна возбуждается источником колебаний частоты ν = 200 Гц и распространяется вдоль оси ОХ. Амплитуда колебаний точек источника ξ0 = 4 мм. Написать уравнение колебаний источника ξ (0, t), если в начальный момент времени смещения точек источника было максимальным. Определить смещение точек среды, которые находятся на расстоянии х = 100 см от источника, в момент времени t = 0,1 с. Скорость звуковой волны принять v = 340 м/с. Затуханием пренебречь. 6. Колебательный контур содержит конденсатор емкостью С = 8 пФ и катушку индуктивностью L = 0,5 мГн. Каково максимальное напряжение U max на обкладках конденсатора, если максимальная сила тока в контуре I max = 40 мА? 7. В вакууме распространяется плоская электромагнитная волна, напряженность электрического поля которой описывается уравнением E = e y E m cos (ω t – kx), где e y – орт оси ОY, E m = 160 В/м, k = 0,51 м-1. Определить напряженность магнитного поля Н волны в точке с координатой х = 7,7 м в момент времени t = 33 нс.
ВАРИАНТ 2
1. Точка совершает колебания по закону синуса с периодом Т = 12 с. В некоторый момент времени смещения х точки равнялось 1 см. Когда фаза колебаний увеличилась вдвое, скорость v точки стала равняться π/6 см/с. Определить амплитуду А колебаний. 2. Точка совершает одновременно два гармонических колебания одинаковой частоты, которые происходят в взаимно перпендикулярных направлениях по уравнениям: х = А 1 cos ω t и y = А 2 sin ω t. Определить уравнение траектории точки. Принять: А 1 = 3 см, А 2 = 1 см. 3. Материальная точка, масса которой m = 50 г, совершает колебания по закону 4. Амплитуда колебаний маятника длиной l = 1 м за время t = 10 мин уменьшилась в два раза. Определить логарифмический декремент l затухания системы. 5. Плоская звуковая волна имеет период Т = 3 мс, амплитуду ξ0 = 0,2 мм и длину волны λ = 1,2 м. Найти скорость точек среды, удаленных от источника колебаний на расстояние х = 2 м, в момент времени t = 7 мс. Начальную фазу колебаний принять равной нулю. 6. Колебательный контур имеет такие параметры: резонансная частота νрез = 600 кГц, емкость конденсатора С = 350 пФ, активное сопротивление R = 15 Ом. Определить добротность контура. 7. В вакууме распространяется плоская электромагнитная волна, амплитуда напряженности магнитного поля которой Н m = 0,1 А/м. Определить интенсивность волны.
ВАРИАНТ 3
1. Точка, которая совершает гармонические колебания по закону x = A cos (ω t + φ) см, в определенный момент времени t 1 имеет смещение x 1 = 4 см, скорость v1= 5 см/c и ускорение a 1 = – 80 см/c2. Определить амплитуду А и период Т колебаний точки; фазу колебаний ω t + φ в момент времени, который рассматривается; максимальные скорость vmax и ускорение a max точки. 2. Складываются два взаимно перпендикулярных колебания, которые выражаются уравнениями х = А 1 sin ω t и y = А 2 cos ω(t + τ), где A 1 = 2 см, A 2 = 1 см, ω = π с–1 , τ = 0,5 с. Найти уравнение траектории. 3. Брусок, масса которого m = 0,5 кг, лежит на гладком столе. Он соединен горизонтальной пружиной жесткостью k = 32 H/мсо стеной. В начальный момент времени пружину сжали на x 0 = 1 см и отпустили. Установить закон движения бруска. Трением пренебречь. 4. Логарифмический декремент l затухания маятника равен 0,01. Определить число N полных колебаний маятника до уменьшения его амплитуды в 3 раза. 5. Поперечная волна распространяется вдоль упругого шнура с скоростью 10 м/с. Амплитуда колебаний точек шнура 5 см, период колебаний 1 с. Записать уравнение волны и определить: 1) длину волны, 2) фазу колебаний, смещение, скорость и ускорение точки, которая удалена на расстояние 9 м от источника колебаний в момент времени t 1 = 2,5 с. 6. На какую длину волны λ будет резонировать контур, который состоит из катушки индуктивностью L = 4 мкГн и конденсатора электроемкостью С = 1,11 нФ? 7. Чему равны амплитуды напряженностей E m и H m электрического и магнитного полей плоской электромагнитной волны в воздухе в фокусе излучения лазера, где интенсивность I = 1014 Вт/см2?
ВАРИАНТ 4
1. Точка совершает колебания по закону x = A cos (ω t + φ), где А = 4 см. Определить начальную фазу φ, если: а) х (0) = 2 см, v(0) < 0; б) х (0) = – 2 см, v(0) < 0; в) х (0) = 2 см, v(0) > 0; г) х (0) = – 2 см, v(0) > 0. Построить векторную диаграмму для момента времени t = 0. 2. Два гармонических колебания одинаковых амплитуд и периодов, которые направлены по одной прямой, складываются в одно колебание той же амплитуды. Найти разность фаз ∆φ складываемых колебаний. 3.Гвоздь забит в стену горизонтально. На него подвешен тонкий обруч, который колеблется в плоскости, параллельной стене. Радиус обруча R = 30 см. Вычислить период T колебаний обруча. 4. Амплитуда затухающих колебаний за время t 1 = 20с уменьшилась в два раза. Во сколько раз она уменьшится за время t 2 = 1 мин? 5. От источника колебаний распространяется гармоническая волна вдоль оси ОХ. Амплитуда ξ0 колебаний равняется 10 см. Каким будет смещение точки, удаленной от источника на х = 3/4 λ, в момент, когда от начала колебаний прошло время t = 0,9 Т? 6. Индуктивность L колебательного контура равняется 0,5 мГн. Какова должна быть электроемкость С контура, чтобы он резонировал на длину волны λ = 300 м? 7. Электромагнитная волна с частотой ν = 4 МГц переходит из немагнитной среды с диэлектрической проницаемостью ε = 3 в вакуум. Определить увеличение ее длины волны.
ВАРИАНТ 5
1. Точка совершает колебания по закону х = А sin (ω t + φ), где А = 4 см. Определить начальную фазу φ, если: х (0) = –2 2. Вычислить возвращающую силу F в момент времени t 1 = 1,25 c и полную механическую энергию Е материальной точки, масса которой m = 10г, а колебания осуществляются по закону 3. Тонкий стержень, подвешенный за конец, совершает колебания с такой же частотой, что и математический маятник длиной l = 1 м. Чему равна длина стержня? 4. Добротность колебательной системы Q = 3, частота свободных колебаний ω = 150 с – 1. Определить собственную частоту ω0 колебаний системы. 5. Определить интенсивность звука (Вт/м2), если уровень громкости его L = 67 дБ. Интенсивность звука на пороге слышимости I 0 = 10–12 Вт/м2. 6. В колебательном контуре происходят свободные незатухающие электромагнитные колебания. Зная, что максимальный заряд конденсатора q m = 10 –6 Кл, амаксимальная сила тока I m = 10А, определить длину волны, на которую резонирует контур. 7. Электромагнитная волна имеет частоту ν = 4∙1014 Гц, длину в некотором веществе λ = 0,1 мкм. Какова скорость распространения волны в этом веществе? Чему равен показатель преломления вещества? Какой будет длина волны после перехода ее в воздух?
ВАРИАНТ 6
1. Максимальная скорость точки, которая совершает гармонические колебания, равняется 10 см/с, максимальное ускорение 100 см/с2. Определить круговую частоту ω колебаний, их период T и амплитуду A. 2. Определить амплитуду А и начальную фазу φ результирующего колебания, которое получится при сложении двух колебаний одинакового направления и периода: х 1 = А 1 sin ω t и х 2 = А 2 sin ω (t + τ), где А 1 = А 2 = 1 см; ω = π с–1, τ = 0,5 с. 3. Айсберг в виде прямой призмы колеблется вдоль вертикальной оси. Определить период Т малых колебаний айсберга, если высота его надводной части h = 100 м. 4. Тело, масса которого m = 1 кг, совершает колебания под действием упругой силы (k = 10 Н/м). Определить коэффициент сопротивления r вязкой среды, если период затухающих колебаний T = 2,1 с. 5. Звуковые колебания с частотой ν = 450 Гц и амплитудой ξ0 = 0,3 мм распространяются в воздухе. Длина волны λ = 80 см. Чему равняется средняя энергия, которая переносится волной в единицу времени через единичную площадку, перпендикулярную направлению волны? Плотность воздуха ρ = 1,29 кг/м3. 6. Емкость конденсатора колебательного контура С = 7 мкФ, индуктивность его катушки L = 0,23 Гн, сопротивление R = 40 Ом. Конденсатору сообщили заряд q 0 = 0,56 мКл и присоединили его к катушке. Определить период колебаний, логарифмический декремент затухания и записать закон изменения напряжения на конденсаторе в зависимости от времени. 7. В колебательном контуре индуктивность катушки можно изменять от 50 до 500 Гн, а емкость конденсатора от 10 до 1000 пФ. Какой диапазон длин волн можно получить при настройке такого контура?
ВАРИАНТ 7
1. Материальная точка, масса которой m = 10 г, осуществляет гармонические колебания по закону косинуса с периодом Т = 2 си начальной фазой φ = 0. Полная механическая энергия точки Е = 0,1 мДж. Определить амплитуду колебаний А и записать закон движения точки. Вычислить максимальное значение F max силы, которая действует на точку. 2. Математический маятник длиной l 1 = 40 см и физический маятник в виде тонкого стержня длиной l 2 = 60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние от центра масс стержня до оси колебаний. 3. Амплитуда затухающих колебаний маятника за время t 1 = 5 мин уменьшилась в два раза. За какое время t 2 амплитуда уменьшится в восемь раз? 4. Груз массой m = 0,5 кг подвешен на пружине, жесткость которой k = 0,49 Н/см, и помещен в масло. Коэффициент сопротивления движению в масле r = 0,5 кг/с. На верхний конец пружины действует вертикальная возмущающая сила, которая изменяется по закону F = 0,98 sinω t,Н.При какой частоте возмущающей силы амплитуда вынужденных колебаний будет максимальной? Чему она равняется? 5. Определить скорость υ распространения волны в упругой среде, если разность фаз ∆φ колебаний двух точек среды, отстоящих друг от друга на ∆ х = 10 см, равняется π/3. Частота колебаний n = 25 Гц. 6. Сила тока в колебательном контуре, который содержит катушку индуктивностью L = 0,1 Гн и конденсатор, с течением времени изменяется по уравнению I = – 0,1 sin 200π t. Определить: 1) период колебаний, 2) емкость конденсатора, 3) максимальное напряжение на обкладках конденсатора, 4) максимальную энергию магнитного поля, 5)максимальную энергию электрического поля. 7. В вакууме вдоль оси ОХ распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны составляет 18,8 В/м. Определить среднюю энергию, которая проходит за t = 1 мин через площадку S = 0,5 м2, размещенную перпендикулярно направлению распространения волны.
ВАРИАНТ 8
1. Определить максимальные значения скорости vmax и ускорения a max точки, которая совершает гармонические колебания с амплитудой A = 3 см и круговой частотой ω = π/2 с–1. 2. Материальная точка массой m = 50 г совершает колебания, уравнение которых имеет вид х = А cos ω t, где А = 10 см, ω = 5 с–1 . Найти силу F, действующую на точку, в двух случаях: 1) в момент, когда фаза ω t = π/3; 2) в положении наибольшего смещения точки. 3. Груз подвешен на пружине, жесткость которой k = 0,1 Н/м, и погружен в среду с коэффициентом сопротивления r = 0,05 кг/с. Масса груза m = 1 кг. Определить добротность Q колебательной системы. 4. Шарик массой m = 50 г колеблется на легкой нити, длина которой l = 1 м. Считая, что коэффициент сопротивления воздуха r = 0,1 кг/с, определить частоту собственных колебаний v 0; резонансную частоту колебаний v рез; резонансную амплитуду A рез, если амплитудное значение возмущающей силы F 0 = 0,01 Н. 5. Плотность некоторого двухатомного газа при нормальном давлении равна 1,78 кг/м3.Определить скорость распространения звука в газе при этих условиях. 6. Напряжение на обкладках конденсатора колебательного контура изменяется по закону U = 30 cos 103π t, B. Емкость конденсатора С = 0,3 мкФ. Определить период Т колебаний, индуктивность катушки L и установить закон изменения силы тока I (t) в контуре. 7. В вакууме вдоль оси ОХ распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны составляет 18,8 В/м. Длина волны l = 31 м. Записать уравнение электромагнитной волны. ВАРИАНТ 9
1. Точка совершает гармонические колебания. Наибольшее смещение x max точки равняется 10 см, наибольшая скорость x max = 20 см/с. Определить круговую частоту ω колебаний. 2. В электронном осциллографе электронный луч отклоняется в двух взаимно перпендикулярных направлениях. Колебания луча описываются уравнениями x = A sin 3ω t, y = A cos 2ω t. Построить траекторию светящейся точки на экране, соблюдая масштаб. Принять А = 4 см. 3. Однородный диск радиусом R = 30 см совершает колебания вокруг горизонтальной оси, которая проходит через одну из образующих цилиндрической поверхности диска. Определить период Т его колебаний. 4. Тело массой m = 0,1 кг подвешено на пружине жесткостью k = 10 H/м. Верхняя часть пружины находится под действием вертикальной силы F = 10–3cos w t, H. Колебания происходят в вязкой среде. Определить максимальную силу трения F т max, которая мешает движению, если при резонансе амплитуда А рез = 0,1 м. 5. Плоская звуковая волна имеет период Т = 3 мс, амплитуду ξ0 = 0,2 мм и длину волны λ = 1,2 м. Для точек среды, удаленных от источника колебаний на расстояние х = 2 м, найти смещение ξ (х, t) в момент t = 7 мс. Начальная фаза колебаний равна нулю. 6. Емкость конденсатора колебательного контура С = 1 мкФ, индуктивность его катушки L = 10 мГн. Какое активное сопротивление R необходимо ввести в контур, чтобы его собственная частота колебаний уменьшилось на 0,01%? 7. Электромагнитные волны распространяются в однородной среде со скоростью 2∙108 м/с. Какую длину волны имеют электромагнитные волны в этой среде, если их частота 1 МГц? ВАРИАНТ 10
1. Груз массой m = 0,1 кг, подвешенный на спиральной пружине, растягивает ее на Δ x = 0,1 мм. Какую амплитуду A будут иметь колебания груза, если полная механическая энергия Е = 1 Дж? 2. Однородный диск радиуса R = 30 см совершает колебания вокруг горизонтальной оси, которая проходит через середину одного из радиусов перпендикулярно к плоскости диска. Определить период Т его колебаний. 3. Груз, масса которого m = 0,1 кг, подвешен на вертикальной пружине жесткостью k = 10 Н/м. Сила сопротивления движения пропорциональна скорости, коэффициент пропорциональности r = 0,87 кг/с. Груз оттянули на x mах = 2 см от положения равновесия и отпу
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.017 с.) |

 ,
, ;
;  .
.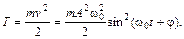

 E = mA 2w02/2.
E = mA 2w02/2.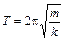 ,
, ,
, .
.

 ,
,  :
:
 ,
, – частота затухающих колебаний, β – коэффициент затухания.
– частота затухающих колебаний, β – коэффициент затухания. ,
, .
. ;
;  .
. .
. .
. .
.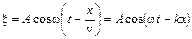 ,
,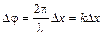 .
. ,
,  ,
, – показатель преломления вещества.
– показатель преломления вещества. .
. .
. , (1)
, (1) . (2)
. (2) .
. , получим
, получим , или
, или  .
. .
.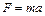 , (3)
, (3) ,
, .
. .
. , то есть
, то есть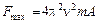 .
. . (4)
. (4) :
: .
. .
. .
. , (1)
, (1) . (2)
. (2) . (3)
. (3) ,
, . Вычисляя, получим l = 70 см.
. Вычисляя, получим l = 70 см. , где А1 = 1 см, А2 = 2 см, ω = π с–1 . Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
, где А1 = 1 см, А2 = 2 см, ω = π с–1 . Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
 поэтому
поэтому .
. то уравнение траектории
то уравнение траектории (1)
(1) Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2).
Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2). . Электроемкость конденсатора С = 0,5 мкФ. Определить период собственных колебаний, индуктивность, энергию контура и максимальную силу тока, текущего по катушке индуктивности.
. Электроемкость конденсатора С = 0,5 мкФ. Определить период собственных колебаний, индуктивность, энергию контура и максимальную силу тока, текущего по катушке индуктивности. ,
, – амплитудное (максимальное) значение напряжения на обкладках конденсатора; w0 – собственная циклическая частота колебаний, которая связана с периодом соотношением
– амплитудное (максимальное) значение напряжения на обкладках конденсатора; w0 – собственная циклическая частота колебаний, которая связана с периодом соотношением .
. .
. , откуда
, откуда  .
. .
. ,
, ,
, .
. .
.
 , (1)
, (1) ,
,
 – условный период затухающих колебаний (
– условный период затухающих колебаний ( – собственная частота контура,
– собственная частота контура,  – коэффициент затухания).
– коэффициент затухания). .
. .
. .
. . (1)
. (1)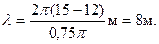
 , l = v T,то
, l = v T,то  .
.
 , (2)
, (2) ;
; .
.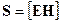 ,
, и
и  – векторы напряженности электрического и магнитного полей в электромагнитной волне.
– векторы напряженности электрического и магнитного полей в электромагнитной волне. , получим для модуля вектора
, получим для модуля вектора и
и  вкаждой точке электромагнитной волны меняются cо временем по закону синуса, находясь в одинаковых фазах, то мгновенное значение величины S равно
вкаждой точке электромагнитной волны меняются cо временем по закону синуса, находясь в одинаковых фазах, то мгновенное значение величины S равно . (1)
. (1) (2)
(2) – энергия, переносимая волной через площадку S плза время
– энергия, переносимая волной через площадку S плза время  .
. . (3)
. (3) .
. .
. , тогда
, тогда . (4).
. (4). .
.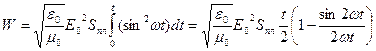 .
. .
. .
.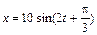 , где х дано в сантиметрах, а аргумент синуса – в радианах. Определить максимальные значения силы F max, возвращающей точку в положение равновесия, и кинетической энергии W к max.
, где х дано в сантиметрах, а аргумент синуса – в радианах. Определить максимальные значения силы F max, возвращающей точку в положение равновесия, и кинетической энергии W к max. см и v(0) > 0. Построить векторную диаграмму для момента t = 0.
см и v(0) > 0. Построить векторную диаграмму для момента t = 0.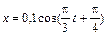 ,м.
,м.


