
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы квантовой физики атомов, физики твёрдого тела и атомного ядраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные ЗАКОНЫ И формулы Элементы квантовой механики ● Длина дебройлевской волны частицы с импульсом р
где m –масса частицы, v – ее скорость. ● Импульс частицы и его связь с кинетической энергией: а) в классическом приближении (v<<c) б) в релятивистском случае где ● Соотношение неопределенностей: а) где б) где ● Вероятность нахождения частицы в объеме d V d W = y y* d V = |y|2 d V, где y = y (x,y,z) – координатная часть волновой функции, y* – функция, комплексно сопряженная с y, |y|2 = y y* – квадрат модуля волновой функции. · Вероятность обнаружения частицы в интервале от х 1 до х 2:
· Одномерное уравнение Шредингера для стационарных состояний:
где · Решение уравнения Шредингера для одномерной, бесконечно глубокой, прямоугольной потенциальной ямы: а) б) где n – квантовое число, номер энергетического уровня, n = 1, 2, 3, …; l – ширина потенциальной ямы. · Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины l
Элементы квантовой статистики и физики твердого тела · Распределение Ферми-Дирака по энергиям для свободных электронов в металле
где < N (E)> – среднее число электронов в квантовом состоянии с энергией Е; k – постоянная Больцмана; T– термодинамическая температура, E F – энергия Ферми. При Т = 0 К
· Характеристическая температура Дебая (при T << T D)
где wD – предельная частота упругих колебаний кристаллической решетки. · Удельная проводимость собственных полупроводников
где g0 – постоянная, характерная для данного полупроводника, D Е – ширина запрещенной зоны.
Элементы физики атомного ядра · Массовое число ядра (число нуклонов в ядре):
где · Энергия связи нуклонов в ядре E св = [ Zm p + (A – Z) m n – m я ] c 2 = [ Zm H + (A – Z) m n – m а] c 2, где m p, m n, m я, – соответственно массы протона, нейтрона и ядра; Z – зарядовое число ядра (число протонов в ядре); А – массовое число; m H – масса атома водорода; m а – масса атома. · Число ядер, распавшихся в среднем за промежуток времени от t до t + d t
· Закон радиоактивного распада:
где · Число ядер, распавшихся за время
В случае если промежуток времени
· Связь периода полураспада с постоянной радиоактивного распада:
· Среднее время t жизни радиоактивного ядра, т. е. интервал времени, за который число нераспавшихся ядер уменьшается в
· Число N атомов, содержащихся в радиоактивном изотопе:
где · Активность нуклида
· Правила смещения: для a -распада для b – -распада
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 6.1. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U1 = 51 B; 2) U2 = 0,51 МВ. Решение. Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой
где h = 6,63∙10 –34 Дж∙с – постоянная Планка. Импульс частицы можно определить, если известна ее кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя, Т << E0) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частиц, T ≈ E 0): в нерелятивистском случае
где в релятивистском случае
где Формула (1) с учетом соотношений (2) и (3) запишется: в нерелятивистском случае
в релятивистском случае
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U 1= 51 B и U 2 = 0,51 МВс энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля. Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U T = | e | U. В первом случае T 1 = 51 эВ = 0,51∙10 –4 МэВ, что много меньше энергии покоя электрона Е 0 = m 0 c 2 = 0,51 МэВ. Следовательно, в этом случае можно применить формулу (4). Вычисляя, получаем λ1 = 171 пм. Во втором случае кинетическая энергия T 2 = 0,51 МэВ равна энергии покоя электрона. В этом случае имеем дело с релятивистской частицей, необходимо применить релятивистскую формулу (5). Учитывая, что
или, учитывая, что h / m 0 c = 2,43 пм есть комптоновская длина волны электрона, получим λ2 = 1,4 пм. Пример 6.2. Используя соотношение неопределенностей Гейзенберга, показать, что ядра атомов не могут содержать электронов. Считать радиус ядра равным 10 –15 м. Решение. Соотношение неопределенностей Гейзенберга выражается формулой
где: Δ х – неопределенность координаты; Δ р х – неопределенность импульса; h – постоянная Планка. Если неопределенность координаты принять равной радиусу ядра, т.е. Δ х = R я, то неопределенность импульса электрона выразим следующим образом: Δ р х = h /(2π Δ х). Так как
Сравнивая полученное значение Δvx со скоростью света в вакууме c = 3∙108 м/с, видим, что Пример 6.3. Электрон в одномерной прямоугольной «потенциальной яме» шириной l = 200 пм с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 4). Определить 1) минимальную энергию электрона; 2) вероятность W обнаружения электрона в первой четверти ямы. Решение. Собственные значения энергии электрона, находящегося на n -м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»
где m = 9,11∙10 –31 кг – масса электрона,
Вероятность обнаружить частицу в интервале х 1 < х < х 2
где
Согласно условию задачи (рис. 6.1) x 1 = 0 и x 2 = l /4. Поэтому, подставив (2) в (1), получим
Заменив sin2(4π x / l) = ½(1 – cos 8π x / l), запишем
Вычисляя, получим: 1) E min = 1,5∙10–18 Дж = 9,37 эВ; 2) W = 0,25. Пример 6.4. Удельная проводимость кремниевого образца при нагревании от температуры t1 = 0°C до температуры t2 = 18°C увеличилась в 4,24 раза. Определить ширину запрещенной зоны кремния. Решение. Удельная проводимость собственных полупроводников
где g0 – постоянная, характерная для данного полупроводника, D Е – ширина запрещенной зоны. Тогда
Или, прологарифмировав,
Откуда искомая ширина запрещенной зоны
Вычисляя, получаем D Е = 1,1 эВ.
Пример 6.5. Вычислить дефект массы и энергию связи ядра Решение. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра
где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов, составляющих ядро); В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому целесообразно пользоваться преобразованной формулой, в которую входит масса
Выразив в равенстве (1) массу ядра, получим
Подставив числовые значения масс, получим
В соответствии с законом пропорциональности массы и энергии
Подставив найденное значение дефекта массы ядра в формулу (2), получим
Пример 6.6. Первоначальная масса радиоактивного изотопа радона 22286 Rn (период полураспада Т1/2 = 3,82 сут) равна 1,5 г. Определить: 1) начальную активность изотопа; 2) его активность через 5 сут. Решение. Начальная активность изотопа A 0 = l N 0 , где l = (ln2)/ T 1/2 – постоянная радиоактивного распада; N 0 – число ядер изотопа в начальный момент времени: N 0 = m 0 N A/M, M – молярная масса радона (M = 222×10–3кг/моль), N A = 6,02×1023 моль–1 – постоянная Авогадро. Учитывая эти выражения, найдем искомую активность изотопа:
Активность изотопа А = l N, где, согласно закону радиоактивного распада,
Вычисляя, получаем: 1) А 0 = 8,54×1015 Бк; 2) А = 3,45×1015 Бк.
КОНТРОЛЬНАЯ РАБОТА №6 ВАРИАНТ 1
1. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля l = 2,02 пм. Определить массу m частицы, если ее заряд численно равен заряду электрона. 2. Определить в электрон-вольтах максимальную энергию Е фонона, который может возбуждаться в кристалле NaCl, если характеристическая температура Дебая T D = 320 К. Фотон какой длины волны λ обладал бы такой энергией? 3. Какую наименьшую энергию Е нужно затратить, чтобы оторвать один нейтрон от ядра азота 147 N? 4. Определить промежуток времени τ, в течение которого активность А изотопа стронция 90Sr уменьшится в k 1 = 10 раз? В k 2 = 100 раз? Период полураспада стронция Т 1/2 = 28 лет. 5. Какая энергия D Е выделяется при термоядерной реакции синтеза 21H + 31H → 42He + 10n? Ответ дать в джоулях и электрон-вольтах.
ВАРИАНТ 2
1. Определить длину волны де Бройля l для: а) электрона, движущегося со скоростью v = 106 м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре Т = 300 К; в) шарика массой m = 1 г, движущегося со скоростью v = 1 см/с. 2. Что такое фонон, каковы его свойства? 3. Энергия связи Е св ядра кислорода 188 O равна 139,8 МэВ, ядра фтора 199 F - 147,8 МэВ. Определить, какую минимальную энергию Е нужно затратить, чтобы оторвать один протон от ядра фтора. 4. Определить массу m полония 210 84Ро, активность которого А = 3,7∙1010 Бк. Период полураспада полония Т 1/2 = 138 сут. 5. Написать недостающие обозначения в реакциях: а) в)
ВАРИАНТ 3
1. Определить дебройлевскую длину волны λ шарика массой m = 1 г, движущегося со скоростью v = 100 м/с. Можно ли обнаружить волновые свойства такого шарика, и почему 2. Объяснить физический смысл энергии Ферми. 3. Определить энергию связи Е св ядра изотопа лития 73Li. 4. Какая часть η начального числа ядер 90Sr распадется за одни сутки и за 15 лет? Какая часть ζ останется через 10 лет и через 100 лет? Период полураспада стронция Т 1/2 = 28 лет. 5. Определить наименьшую энергию g-кванта, достаточную для осуществления реакции разложения дейтона g-лучами
ВАРИАНТ 4
1. Определить квантовомеханическую неопределенность Δ v x х -компоненты скорости частицы массой m = 1 г и электрона, если положение каждого из них определено с одинаковой ошибкой ∆ х = 10–7м. 2. Пояснить физический смысл характеристической температуры Дебая. 3. Определить энергию связи Е св ядра атома гелия 42He. 4. Вследствие последовательных радиоактивных распадов ядро урана 5. При бомбардировке изотопа азота
ВАРИАНТ 5
1. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить (в электрон-вольтах) неопределенность кинетической энергии этого электрона. 2. В германии с примесью бора энергия активации примесных атомов Δ Е п = 0,01 эВ. Определить: 1) тип проводимости примесного полупроводника; 2) тип примесной фотопроводимости; 3) красную границу фотопроводимости. 3. Определить энергию связи Е св ядра атома алюминия 4. Определить постоянную радиоактивного распада λ ядра 55Co, если за час распадается 4% начального числа ядер. Продукт распада стабильный. 5. Определить суточный расход ядерного горючего 235U в реакторе АЭС. Тепловая мощность станции равна Р = 10 МВт. Принять, что в одном акте деления выделяется энергия Q = 200 МэВ, а КПД станции равен η = 0,2 (20%).
ВАРИАНТ 6
1. Электрон находится в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l. Определить, в каких точках интервала ( 2. В чем смысл понятия «дырка» как носителя тока в полупроводнике? Существуют ли дырки вне полупроводника? Совпадают ли зоны проводимости для электронов и дырок в полупроводниках? Чему равна наименьшая энергия emin образования пары электрон-дырка в собственном полупроводнике, проводимость которого возрастает в n = 2 раза при повышении температуры от T 1 = 300 K до T 2= 310 К? 3. Определить энергию связи Е св ядер: а) 4. За один год начальное количество радиоактивного препарата уменьшилось в 5 раз. Во сколько раз оно уменьшится за два года? 5. Определить энергию Е, которая высвободится при соединении одного протона и двух нейтронов в атомное ядро.
ВАРИАНТ 7
1. Электрон в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l находится в нижнем возбужденном состоянии. Какова вероятность обнаружения электрона в интервале l /4, равноудаленном от стенок ямы? 2. Определить ширину D Е запрещенной зоны теллура, если его электропроводность возрастает в n = 5 раз при повышении температуры от T 1=300 K до T 2= 400 K. 3. Определить энергию связи Е св, приходящуюся на один нуклон в ядрах; a) 4. Определить количество D N атомов, которые распались в m = 1 мг радиоактивного натрия 2411Na за время t 1= 10 час. Период полураспада натрия Т 1/2= 15,3 час. 5. Определить энергию Q ядерной реакции: 4420Са +11Н→4119К+42He.
ВАРИАНТ 8
1. Частица в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l находится в основном состоянии, которому соответствует энергия Е 1 = 8,12 МэВ. Ширина ямы l = 5∙10–15 м. Определить массу m частицы. 2. Кремниевый образец нагревают от 0 до 10 °С. Принимая ширину D Е запрещенной зоны кремния 1,1 эВ, определить, во сколько раз возрастет его удельная проводимость. 3. Энергия связи Е св ядра, состоящего из двух протонов и одного нейтрона, равна 7,72 МэВ. Определить массу m a нейтрального атома, имеющего это ядро. 4. Сколько атомов из N = 106 атомов полония распадается за время t = 1 сут? Период полураспада полония Т 1/2 = 138 сут. 5. Определить энергию Q, выделяющуюся при реакции
ВАРИАНТ 9
1. Рассматривая приближенно ядро и атом как одномерные прямоугольные бесконечно глубокие потенциальные ямы для электронов и нуклонов, вычислить расстояние между основным и первым возбужденным уровнями в атоме Δ Е а1,2 и ядре Δ Е я1,2, полагая, что для атома l а = 5∙10–10 м, а для ядра l я = 5∙10–15 м. 2. Удельная проводимость кремния имеет значение σ1 =19 См/м при температуре T 1= 600 Kи σ2 =4 095 См/м при T 2= 1 200 K. Определить ширину D Е запрещенной зоны для кремния. 3. Определить массу m a нейтрального атома, если ядро этого атома состоит из трех протонов и двух нейтронов и энергия связи Е св ядра равна 26,3 МэВ. 4. За время t =1 сут активность изотопа уменьшилась от А 1 = 118 ГБк до А 2 = 7,4 ГБк. Определить период полураспада T 1/2 этого нуклида. 5. Определить энергию Q, поглощающуюся при реакции
ВАРИАНТ 10
1. Электрон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U 0 = 10 эВ и шириной l = 0,1 нм. Определить для этого барьера коэффициент прозрачности D. 2. В кремнии с примесью мышьяка энергия активации примесных атомов Δ Е п = 0,05 эВ. Определить: 1) тип проводимости примесного полупроводника; 2) тип примесной фотопроводимости; 3) максимальную длину волны, при которой фотопроводимость еще возбуждается. 3. Определить энергию связи, приходящуюся на один нуклон Е св/ A в ядрах; a) 73 Li; б) 147 N; в) 2713 А1; г) 4020 Са; д) 6329 Cu; e) 11348 Cd; ж) 20080 Hg; з) 23892 U. Построить зависимость Е св/ A = ƒ(А), где А – массовое число. 4. Определить постоянную распада λ радона, если известно, что число атомов радона уменьшается за время t = 1 сут на 18,2%. 5. Определить энергию Q, выделяющуюся при реакции: Приложения
I. Таблицы физических величин
1. Единицы физических величин (СИ)
2. Множители и приставки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 890; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.205.182 (0.016 с.) |


 ;
;  ,
, ;
;  ,
, – масса покоя частицы;
– масса покоя частицы;  – релятивистская масса;
– релятивистская масса;  – скорость частицы;
– скорость частицы;  – скорость света в вакууме;
– скорость света в вакууме;  – энергия покоя частицы
– энергия покоя частицы 
 , (для координаты и импульса);
, (для координаты и импульса); – неопределенности проекции импульса на ось х; Δ x – неопределенность координаты,
– неопределенности проекции импульса на ось х; Δ x – неопределенность координаты,  – постоянная Планка.
– постоянная Планка. , (для энергии и времени),
, (для энергии и времени),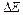 – неопределенность энергии данного квантового состояния;
– неопределенность энергии данного квантового состояния;  – время пребывания системы в данном энергетическом состоянии.
– время пребывания системы в данном энергетическом состоянии. .
. ,
, – волновая функция, описывающая состояние частицы; m – масса частицы; E – полная энергия;
– волновая функция, описывающая состояние частицы; m – масса частицы; E – полная энергия; 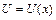 – потенциальная энергия частицы.
– потенциальная энергия частицы. (собственная нормированная волновая функция);
(собственная нормированная волновая функция); (собственное значение энергии частицы),
(собственное значение энергии частицы), .
. ,
,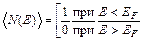 .
. ,
, ,
, ,
, – зарядовое число (число протонов);
– зарядовое число (число протонов); 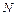 – число нейтронов.
– число нейтронов. .
. ,
, – число ядер, распадающихся за интервал времени
– число ядер, распадающихся за интервал времени  ;
;  ;
;  – число ядер в начальный момент
– число ядер в начальный момент  ;
;  – постоянная радиоактивного распада.
– постоянная радиоактивного распада.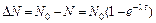 .
. , то число распавшихся ядер можно определить по формуле
, то число распавшихся ядер можно определить по формуле .
.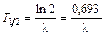 .
. раз:
раз: .
.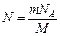 ,
, – молярная масса;
– молярная масса;  – постоянная Авогадро.
– постоянная Авогадро. .
. ,
, .
.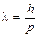 , (1)
, (1) (2)
(2) (3)
(3) – энергия покоя частицы.
– энергия покоя частицы. (4)
(4) . (5)
. (5) , по формуле (5) находим
, по формуле (5) находим
 ,
, , то
, то  и
и  . Вычислим неопределенность скорости электрона:
. Вычислим неопределенность скорости электрона:
 , а это невозможно, следовательно, ядра не могут содержать электронов.
, а это невозможно, следовательно, ядра не могут содержать электронов. ,
, = 1,05∙10–34 Дж∙с – постоянная Планка. Минимальную энергию электрон имеет при минимальном n, т.е. при n = 1:
= 1,05∙10–34 Дж∙с – постоянная Планка. Минимальную энергию электрон имеет при минимальном n, т.е. при n = 1: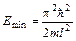 .
. , (1)
, (1) – нормированная собственная волновая функция, соответствующая данному состоянию.
– нормированная собственная волновая функция, соответствующая данному состоянию. Возбужденному состоянию n = 4 отвечает собственная функция
Возбужденному состоянию n = 4 отвечает собственная функция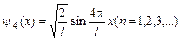 . (2)
. (2) .
.
 ,
, .
. .
. .
. .
. и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е.
и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е. (1)
(1) – соответственно массы протона, нейтрона и ядра.
– соответственно массы протона, нейтрона и ядра.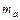 нейтрального атома:
нейтрального атома: откуда
откуда  .
. или
или 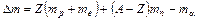 . Замечая, что
. Замечая, что  , где
, где  - масса атома водорода, окончательно находим
- масса атома водорода, окончательно находим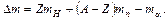
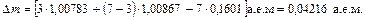 .
. где с – скорость света в вакууме. Коэффициент пропорциональности
где с – скорость света в вакууме. Коэффициент пропорциональности  может быть выражен двояко:
может быть выражен двояко: 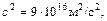 или
или  Если вычислять энергию связи, пользуясь внесистемными единицами, то
Если вычислять энергию связи, пользуясь внесистемными единицами, то  . С учетом этого
. С учетом этого (2)
(2) .
.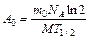 .
. – число нераспавшихся ядер в момент времени t. Учитывая, что А0 = l N0, найдем, что активность нуклида уменьшается со временем по закону
– число нераспавшихся ядер в момент времени t. Учитывая, что А0 = l N0, найдем, что активность нуклида уменьшается со временем по закону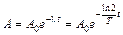 .
. а.е.м.
а.е.м.  а.е.м.
а.е.м.  а.е.м.
а.е.м.
 а.е.м.
а.е.м. ; б)
; б)  ;
; ; г)
; г)  .
. .
.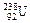 превратилось в ядро свинца
превратилось в ядро свинца  . Пользуясь таблицей Менделеева, определить сколько актов α-распада и β-распада при этом произошло.
. Пользуясь таблицей Менделеева, определить сколько актов α-распада и β-распада при этом произошло. нейтронами получается изотоп углерода
нейтронами получается изотоп углерода  , который оказывается b - радиоактивным. Написать уравнения обеих реакций.
, который оказывается b - радиоактивным. Написать уравнения обеих реакций. .
. ) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова. Вычислить плотность вероятности для этих точек. Пояснить графически.
) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова. Вычислить плотность вероятности для этих точек. Пояснить графически. ; б)
; б)  . Какое из этих ядер более устойчиво?
. Какое из этих ядер более устойчиво? ; б)
; б) 

 .
.


