
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика материальной точки и поступательного движения твердого телаСодержание книги
Поиск на нашем сайте
· Импульс материальной точки
· Второй закон Ньютона (основное уравнение динамики материальной точки) F = m a = где F – результирующая сила, действующаяна материальную точку. · Силы, рассматриваемыев механике: а) сила тяжести
б) сила гравитационного взаимодействия (закон всемирного тяготения)
где F – сила взаимного притяжения двух материальных точек массами m 1 и m 2; G – гравитационная постоянная; r – расстояние между точками. в) сила упругости (закон Гука для продольного растяжения или сжатия) F x = – kx, или σ = ε Е, где F x – проекция упругой силы на ось х, k – коэффициент упругости (в случае пружины – жесткость), х– деформация; σ = F упр / S – нормальное напряжение, S – площадь поперечного сечения, ε = x / l – относительная деформация, l – начальная длина тела, Е – модуль Юнга. г) сила трения скольжения F тр = m N, где m – коэффициент трения скольжения; N – сила нормального давления. · Закон сохранения импульса для замкнутой системы тел
· Работа, совершаемая постоянной силой, dA = F s ds = F ds cosα, где α – угол между направлением силы и перемещения. · Работа переменной силы на пути s
· Мгновенная мощность
· Кинетическая энергия тела, движущегося поступательно,
· Потенциальная энергия: а) упруго деформированной пружины
б) гравитационного взаимодействия двух материальных точек
в) тела, поднятого над поверхностью Земли на высоту h
где g – ускорение свободного падения (формула справедлива при условии h<<R, где R – радиус Земли). · Закон сохранения механической энергии (выполняется в замкнутой системе, в которой действуют только консервативные силы)
· Работа A результирующей всех сил равна приращению кинетической энергии материальной точки:
· Работа A консервативных сил равна убыли потенциальной энергии материальной точки:
1.4. Динамика вращения вокруг неподвижной оси · Момент инерции материальной точки относительно оси Оz Jz = mr 2, где m – масса материальной точки, r – расстояние от нее до оси Оz. · Момент инерции твердого тела относительно оси Оz
где ri – расстояние i -го элемента массы m i до оси Оz.. В случае непрерывного распределения масс
Моментыинерции некоторых тел правильной геометрической формы:
· Момент инерции тела относительно произвольной оси (теорема Штейнера)
где · Момент силы относительно оси вращения Oz M z = F ┴ l, где F┴ – проекция силы на плоскость, перпендикулярную оси Oz, l – плечо силы (кратчайшее расстояние от оси вращения до линии действия силы). · Момент импульса твердого тела относительно неподвижной оси вращения Oz
где Jz – момент инерции относительно оси вращения, ω – угловая скорость. · Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z
где Мz – результирующий момент относительно оси Оz внешних сил, действующих на тело; ε – угловое ускорение; Jz – момент инерции твердого тела относительно оси вращения. · Если Мz = 0 (система замкнута), то имеет место закон сохранения момента импульса относительно оси Оz
· Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
· Работа при вращательном движении
где · Кинетическая энергия тела, катящегося по плоскости
где vc – скорость центра масс, J c – момент инерции тела относительно оси, проходящей через центр масс. Релятивистская механика · Во всех задачах считается, что система отсчета К′ движется со скоростью v в положительном направлении оси Ох системы К, причем оси Ох ′ и Ох совпадают, а оси Оу ′ и Оу, а также Oz ′ и Oz параллельны. · Релятивистское сокращение длины стержня
где l 0 – длина стержня, измеренная в системе координат, относительно которой стержень покоится, l – длина стержня, измеренная в системе координат, относительно которой он движется со скоростью v. · Релятивистское замедление хода часов
где Δ t 0 – интервал времени между двумя событиями, происходящими в одной точке системы К ′, измеренный по часам этой системы (движущимся вместе с телом), Δ t – интервал времени между двумя событиями, измеренный по часам системы К, относительно которой тело движется со скоростью v. · Релятивистский закон сложения скоростей
где v′ – скорость тела относительно системы К ′; v0 – скорость системы К ′ относительно К, v – скорость тела относительно системы К. · Релятивистская масса и релятивистский импульс
где m 0 – масса покоя. · Полная энергия релятивистской частицы E = mc 2 = m 0 c 2 + T, T = (m – m 0) c 2, где Т – кинетическая энергия частицы, m 0 c 2 = Е 0 – ее энергия покоя. · Связь между энергией и импульсом релятивистской частицы E 2 = m 02 c 4 + p 2 c 2, p 2 c 2 = T (T – 2 E 0).
Примеры решения задач Пример 1.1. С башни в горизонтальном направлении брошено тело с начальной скоростью v0 = 10 м/с. Пренебрегая сопротивлением воздуха, определить для момента времени t = 2 с после начала движения:1) скорость тела;2) радиус кривизны его траектории. Решение.
Отметим, что для свободного полета полное ускорение всегда равно g – ускорению свободного падения. Разложим вектор g на нормальное a n и тангенциальное a τ ускорения. Из рисунка видно, что
С другой стороны, a n = v2/ R, откуда
Вычисляя, получаем: 1) v = 22 м/с; 2) R = 109 м. Пример 1.2. Скорость материальной точки изменяется по закону Решение. Скорость материальной точкизадана в задаче как вектор v = vx i + vy j. Модуль вектора скорости равен
Компоненты вектора скорости есть производные по времени от компонент радиус-вектора
Из соотношения
Аналогично находится
Модуль перемещения
Ускорение определяется производной от вектора скорости по времени, то есть
Модуль вектора а найдем по формуле
Подставив числовые значения, получим: Δ r = 28,5 м; Пример 1.3. Тело вращается вокруг неподвижной оси по закону φ = A + Bt + Ct2, где А = 10 рад, В = 20 рад/с, С = – 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения, для момента времени t = 4 с. Решение. Все точки вращающегося тела описывают окружности. Полное ускорение a точки, движущейся по окружности, может быть найдено как векторная сумма тангенциального ускорения a = a n + a τ. Так как векторы a n и a τ взаимно перпендикулярны, то модуль их суммы
Используем формулы, выражающие связь линейных и угловых величин,
где ω– модуль угловой скорости тела; ε – модуль его углового ускорения. Тогда
Модуль угловой скорости ω найдем, взяв первую производную от угла поворота по времени:
Для момента времени t = 4 с модуль угловой скорости ω = [20 + 2(–2)4] рад/с = 4 рад/с. Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
Подставляя значения ω, ε и r в формулу (2), получаем a = Пример 1.4. При выстреле из пружинного пистолета вертикально вверх пуля массой т = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на х = 10 см. Массой пружины и силами трения пренебречь. Решение. Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы (тяжести и упругой деформации пружины), то для решения задачи можно применить закон сохранения механической энергии. Согласно ему полная механическая энергия системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии в конечном состоянии (когда пуля поднялась на высоту h), т. е.
где T 1, T 2, П 1 и П 2 – кинетические и потенциальные энергии системы в начальном и конечном состояниях. Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид
Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т. е.
а в конечном состоянии – потенциальной энергии пули на высоте h, т. е.
Подставив выражения П 1 и П 2 в формулу (2), найдем
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим единицы их измерения:
Убедившись, что полученная единица является единицей жесткости (1 Н/м), подставим в формулу (3) значения величин и произведем вычисления:
Пример 1.5. Шар массой m1, движущийся горизонтально с некоторой скоростью v1, столкнулся с неподвижным шаром массой m2. Удар прямой,центральный, абсолютно упругий. Какую долю e своей кинетической энергии первый шар передал второму? Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
где Т 1 – кинетическая энергия первого шара до удара; u 2 и Т 2 – скорость и кинетическая энергия второго шара после удара. Как видно из формулы (1), для определения ε надо найти u 2. Так как удар шаров абсолютно упругий, то механическая энергия тел не переходит в другие виды энергии, выполняются законы сохранения импульса и механической энергии:
Здесь v – скорости тел до удара (v2 = 0), u – после удара. Решим совместно уравнения (2) и (3):
Подставив выражение u 2 в формулу (1) и сократив на v1 и т 1, получим
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Пример 1.6. Сила тяги автомобиля изменяется с расстоянием по закону F = A + Bs + Cs2, где A = 1 кН, B = 0,5 кН/м, C = 0,3 кН/м2. Определить работу силы тяги на участке пути s = 10 м и среднюю мощность автомобиля, если разгон длился t = 2 с. Решение. Работа, совершаемая переменной силой, на пути s
где α – угол между направлениями силы и перемещения. Очевидно, что сила тяги действует вдоль перемещения, поэтому α = 0, cos α = 1. Интегрируя, получим
Подставляя числа, найдем А = 1,35×105 Дж. Средняя мощность, развиваемая автомобилем
Вычисляя, получим < N > = 67,5 кВт. Пример 1.7. Через блок в виде сплошного диска, имеющего массу m = 80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами т1 = 100 г и т2 = 200 г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь. Решение. Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести mg и сила T натяжения нити. Напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на вертикаль. Для первого груза T 1 – m 1 g = m 1 a; (1) для второго груза
M = I ε. (3) Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона силы Т′ 1 и Т′ 2, приложенные к ободу диска, равны соответственно силам Т 1 и Т 2, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке, следовательно, Т′ 2 >Т′ 1. Вращающий момент, приложенный к диску, М = (Т′ 2 –Т′ 1) r. Подставив в формулу (3) выражения М, углового ускорения ε = a / r, и момента инерции блока (сплошного диска) I = (½) mr 2, получим (Т′ 2 –Т′ 1) r = Согласно третьему закону Ньютона, с учетом невесомости и нерастяжимости нити, Т' 1 = Т 1, T' 2 = Т 2. Воспользовавшись этим, подставим в уравнение (4) вместо Т¢ 1 и Т¢ 2выражения Т 1и T 2, получив их предварительно из уравнений (1) и (2),
После сокращения на r и перегруппировки членов найдем
После подстановки числовых значений, получим а = 2,88 м/с2. Пример 1.8. Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n1 = 480 мин-1 и предоставлен сам себе. Под действием сил трения маховик остановился через t = 50 с. Найти момент М сил трения. Решение. Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде
где dLz – изменение проекции на ось Оz момента импульса маховика, вращающегося относительно оси Оz, совпадающей с геометрической осью маховика, за интервал времени dt; Mz – момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно оси Оz.
Момент сил трения можно считать не изменяющимся с течением времени (M z = const), поэтому интегрирование уравнения (1) приводит к выражению
При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса равно
где Jz – момент инерции маховика относительно оси Оz; ∆ω – изменение угловой скорости маховика. Приравняв правые части равенств (2) и (3), получим
Момент инерции маховика в виде сплошного диска определяется по формуле
Изменение угловой скорости ∆ω = ω2 – ω1выразим через конечную n 2 и начальную n 1 частоту вращения, пользуясь соотношением ω = 2 π n:
Подставив в формулу (4) выражения Jz и ∆ω, получим
Проверим, дает ли расчетная формула единицу момента силы (Н·м). Для этого в правую часть формулы вместо символов величин подставим их единицы:
Подставим в (5) числовые значения величин и произведем вычисления, учитывая,что n1 = 480 мин-1= (480/60) с-1 = 8 с-1.
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие. Пример 1.9. Платформа в виде сплошного диска радиусом R = 1,5 м и массой m1 = 180 кг вращается около вертикальной оси с частотой n =10 мин-1. В центре платформы стоит человек массой т2 = 60 кг. Какую линейную скорость v относительно пола помещения будет иметь человек, если он перейдет на край платформы? Решение. Согласно условию задачи, момент внешних сил относительно оси вращения Oz, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция Lz момента импульса системы платформа – человек остается постоянной:
где Jz – момент инерции платформы с человеком относительно оси z, ω – угловая скорость платформы. Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии Jz = J 1 + J 2, а в конечном состоянии Jz ¢ = J 1¢ + J 2¢ С учетом этого равенство (1) примет вид
где значения моментов инерции J 1 и J 2 платформы и человека, соответственно, относятся к начальному состоянию системы; J 1¢и J 2¢ – к конечному. Момент инерции платформы относительно оси Оz при переходе человека не изменяется: J 1 = J¢ 1 = ½ m 1 R2. Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J 2 в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека J¢ 2 = m 2 R 2. Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (ω = 2π n) и конечной угловой скорости (ω ' = v /R, где v – скорость человека относительно пола):
После сокращения на R 2 и простых преобразований находим скорость:
Произведем вычисления
Пример 1.10. Определить, какая кинетическая энергия должна быть сообщена ракете массой m0 = 1,5 т, чтобы она приобрела скорость v = 120 Мм/с. Решение. Кинетическая э нергия ракеты T = (m – m 0) c 2, где Из этих выражений получаем, что
Вычисляя, получаем Т = 1,23×1019 Дж.
КОНТРОЛЬНАЯ РАБОТА №1
ВАРИАНТ 1
1. Начальная скорость частицы v 1 = 1 i + 3 j + 5 k (м/с), конечная – v 2 = 2 i + 4 j + 6 k (м/с). Определить: а) приращение скорости Δ v; б) модуль приращения скорости │Δ v │; в) приращение модуля скорости Δ v. 2. Движения двух материальных точек выражаются уравнениями x 1 = A 1 + B 1 t + C 1 t 2, x 2 = A 2 + B 2 t + C 2 t 2, где A 1 = 20 м; A 2 = 2 м, В 1 = В 2 = 2 м/с; С 1 = 4 м/с2; С 2 = 0,5 м/с2. В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v 1 и v 2 и ускорения а 1 и а 2 точек в этот момент 3. Колесо вращается с постоянным угловым ускорением e = 3 рад/с2. Определить радиус колеса, если через t = 1 с после начала движения полное ускорение точки на ободе колеса а = 7,5 м/с2. 4. Две одинаковых тележки массой M каждая движутся по инерции (без трения) друг за другом с одинаковой скоростью v0. B какой-то момент времени человек массой m, находящийся на задней тележке, прыгнул в переднюю со скоростью u относительно своей тележки. Определить скорость v 5. Тонкий однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением ε = 3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент M. 6. Полый тонкостенный цилиндр катится вдоль горизонтального участка дороги со скоростью v =1,5 м/с. Определить путь, который он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути. 7. Две релятивистские частицы движутся в лабораторной системе отсчета навстречу друг другу вдоль одной прямой со скоростями v1 = 0,6 с и v2 = 0,9 с. Определить их относительную скорость.
ВАРИАНТ 2
1. Радиус-вектор материальной точки изменяется со временем по закону r = 4 t 2 i + 3 t j + 2 k (м). Определить: 1) скорость точки v; 2) ускорение точки а; 3) модуль скорости точки в момент времени t = 2 с. 2. Якорь электродвигателя, имеющий частоту вращения n = 50 с-1, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение e якоря. 3. К пружинным весам подвешен блок. Через блок перекинут шнур, к концам которого привязали грузы массами m 1 = 1,5 кг и m 2 = 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь. 4. Платформа с песком общей массой M = 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8 кг и застревает в нем. Пренебрегая трением, определить, с какой скоростью будет двигаться платформа, если снаряд падает сверху вниз под углом α= 30° к горизонту со скоростью v= 450 м/с. 5. Сплошной однородный диск скатывается без скольжения по наклонной плоскости, образующей угол α с горизонтом. Определить линейное ускорение а центра диска. 6. Маховик, момент инерции которого J = 40 кг∙м2, начал вращаться равноускоренно из состояния покоя под действием момента силы М = 20 Н∙м.. Определить кинетическую энергию Т, приобретенную маховиком через t = 10 с. 7. Время жизни покоящегося мюона τ0 = 2,2 мкс. От точки рождения до детектора, зарегистрировавшего его распад, мюон пролетел расстояние l = 6 км. С какой скоростью v (в долях скорости света) двигался мюон?
ВАРИАНТ 3
1. Материальная точка движется вдоль прямой так, что ее ускорение линейно растет и за первые t = 10 с достигает значения a = 5 м/с2. Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь. 2. Колесо автомашины вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин––1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. 3. Пуля массой т = 10 г, летящая горизонтально со скоростью v= 0,5 км/с, попадает в подвешенный на тросах ящик с песком массой M = 6 кг и застревает в нем. Определить высоту h, на которую поднимется такой баллистический маятник, отклонившись после удара. 4. Тело массой m = 0,4 кг соскальзывает без начальной скорости по наклонной плоскости высотой h = 10 см и длиной l = 1 м и, пройдя по горизонтальной плоскости некоторый путь, останавливается. Коэффициент трения на всем пути f = 0,04. Определить: 1) кинетическую энергию тела у основания плоскости; 2) путь, пройденный телом на горизонтальном участке до остановки. 5. На вращающейся вокруг вертикальной оси платформе стоит человек и держит в руках стержень длиной l = 2,4 м и массой m = 8 кг, расположенный вертикально по оси вращения платформы. Платформа с человеком вращается с частотой n 1 = 1 с –1. С какой частотой n 2 будет вращаться платформа с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и платформы равен 6 кг×м2. 6. Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε = 0,4 рад/с2. Определить кинетическую энергию маховика через время t 2 = 25 с после начала движения, если через t 1 = 10 с после начала движения момент импульса L 1 маховика составлял 60 кг∙м2/с. 7. Вычислить энергию покоя: 1) электрона; 2) протона; 3) α-частицы. Ответ выразить в джоулях и мегаэлектрон-вольтах.
ВАРИАНТ 4
1. Уравнение прямолинейного движения тела имеет вид х = At – Вt 2 + Сt 3 (A = 2 м/с, B = 3 м/с2, С = 4 м/с3). Записать выражения для скорости и ускорения. Определить для момента времени t = 2 с после начала движения: 1) пройденный путь; 2) скорость; 3) ускорение. 2. Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением а t. К концу четвертого оборота после начала движения линейная скорость точки u = 15 см/с. Определить нормальное ускорение а n точки через t = 16 с после начала движения. 3. Пуля массой т = 10 г, летящая горизонтально, попадает в подвешенный на тросах длиной l =1 м ящик с песком массой M = 1,5 кг и застревает в нем. Такой баллистический маятник отклонился после удара на угол φ = 30°. Определить скорость пули. 4. Найти работу А подъема груза по наклонной плоскости длиной l = 2 м, если масса груза m = 100 кг, угол наклона наклонной плоскости j = 30°, коэффициент трения f = 0,1, и груз движется с ускорением а = 1 м/с2. 5. Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению φ = A + Bt 2 + Ct 3 (B = 2 рад/с2, C = –0,5 рад/с3). Определить момент вращающей силы M для t = 3 с. 6. Горизонтальная платформа массой m = 25 кг и радиусом R = 0,8 м вращается с частотой n 1 = 18 мин–1. В центре стоит человек и держит на вытянутых руках гантели. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J 1 = 3,5 кг∙м2 до J 2 = 1 кг∙м2. 7. Полная энергия тела возросла на ∆ Е = 1 Дж. На сколько при этом изменилась масса тела?
ВАРИАНТ 5
1. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t = 2 с камень упал на землю на расстоянии s = 40 м от основания вышки. Определить начальную v0 и конечную v скорости камня. 2. Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A + Bt + Ct 2 + Dt 3 (В = 1 рад/с, С = 1 рад/с2, D = 1 рад/с3). Определить для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение a t; 2) нормальное ускорение а n; 3) полное ускорение а. 3. Материальная точка массой m = 1 кг, двигаясь равномерно, описывает четверть окружности радиуса r = 1,2 м в течении времени t = 2 с. Найти изменение ∆р импульса точки. 4. Пуля массой т = 10 г, летящая горизонтально со скоростью v = 200 м/с, попадает в подвешенный на тросах длиной l =1 м ящик с песком массой M = 1,5 кг и застревает в нем. Определить угол отклонения φ такого баллистического маятника. 5. Сплошной цилиндр массой m = 4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость центра масс цилиндра v = 1 м/с. Определить полную кинетическую энергию Т цилиндра. 6. На вращающейся вокруг вертикальной оси платформе стоит человек и держит в руках стержень длиной l = 2,5 м и массой m = 8 кг, расположенный вертикально по оси вращения платформы. Платформа с человеком вращается с частотой n 1 = 12 мин–1. С какой частотой n 2 будет вращаться платформа с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и платформы равен 10 кг×м2. 7. На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость v 0 спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике за время τ0 = 0,5 года по часам земного наблюдателя?
ВАРИАНТ 6
1. Радиус-вектор материальной точки изменяется со временем по закону r = Аt 2 i + Вt j + С k, где А = 2 м/с2; В = 5 м/с; С = 3 м. Определить: 1) скорость v; 2) ускорение а; 3) модуль скорости v в момент времени t = 4 с. 2. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением j = At 2 (А = 0,5 рад/с2). Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное а t, нормальное а n и полное а ускорения. 3. По наклонной плоскости с углом наклона α = 30° к горизонту скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения f = 0,15. 4. Пуля массой m = 10 г, летящая с горизонтальной скоростью v= 0,6 км/с, попадает в мешок с песком массой M = 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) долю кинетической энергии, израсходованной на пробивание песка. 5. Шар и сплошной цилиндр одинаковой массы, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра. 6. Человек массой m = 60 кг, стоит на краю горизонтальной платформы массой M = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n 1 = 10 мин-1. Считая платформу круглым однородным диском, а человека – точечной массой, определить, с какой частотой n 2 будет вращаться платформа, если человек перейдет к ее центру. 7. Электрон движется со скоростью v = 0,6 с. Определить релятивистский импульс р электрона.
ВАРИАНТ 7
1. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от време
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.236.206 (0.018 с.) |

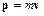 .
. ,
, ;
; ,
, .
. .
. .
. , или
, или  .
. ,
, ,
, ,
, .
. .
. .
.





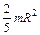
 ,
, – момент инерции тела относительно оси, проходящей через центр масс тела параллельно заданной оси; а – расстояние между осями; т – масса тела.
– момент инерции тела относительно оси, проходящей через центр масс тела параллельно заданной оси; а – расстояние между осями; т – масса тела. ,
,
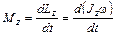 , или
, или 
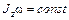 .
. .
. ,
, – угол поворота тела.
– угол поворота тела. ,
, ,
, ,
, ,
, ,
,  ,
, Предположим, что через t = 2 с после начала движения тело находится в точке A. Проведем в этой точке по касательной к траектории вектор мгновенной скорости и разложим его на горизонтальную v x и вертикальную v y составляющие (рис. 1.2). Тело участвует в двух взаимно перпендикулярных движениях: равномерном прямолинейном движении вдоль оси Ох (со скоростью vx = v0) и свободном падении вдоль оси Оу (со скоростью vy = gt). Следовательно, скорость тела в точке А
Предположим, что через t = 2 с после начала движения тело находится в точке A. Проведем в этой точке по касательной к траектории вектор мгновенной скорости и разложим его на горизонтальную v x и вертикальную v y составляющие (рис. 1.2). Тело участвует в двух взаимно перпендикулярных движениях: равномерном прямолинейном движении вдоль оси Ох (со скоростью vx = v0) и свободном падении вдоль оси Оу (со скоростью vy = gt). Следовательно, скорость тела в точке А
 .
.
 .
. ,(м/с), i и j – орты осей х и у. Определить в момент времени t = 2 c после начала движения:1) модуль перемещения; 2) модуль скорости; 3) модуль ускорения.
,(м/с), i и j – орты осей х и у. Определить в момент времени t = 2 c после начала движения:1) модуль перемещения; 2) модуль скорости; 3) модуль ускорения.
 = vx i + vy j.
= vx i + vy j. следует, что
следует, что .
.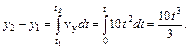
 .
.
 .
.
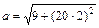 = 40,1 м/с2.
= 40,1 м/с2. , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения  , направленного к центру кривизны траектории (рис. 1.1):
, направленного к центру кривизны траектории (рис. 1.1): . (1)
. (1) ,
,  ,
, (2)
(2)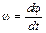 = B + 2 Ct.
= B + 2 Ct. = 2 С = – 4 рад/с2.
= 2 С = – 4 рад/с2.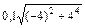 м/с2 =1,65 м/с2.
м/с2 =1,65 м/с2. , (1)
, (1) . (2)
. (2) ,
, .
. . (3)
. (3) .
. .
. (1)
(1) ; (2)
; (2) (3)
(3)

 ,
, .
. .
. . (2)
. (2) Согласно основному уравнению динамики вращательного движения, вращающий момент М, приложенный к диску, равен произведению момента инерции I диска на его угловое ускорение ε:
Согласно основному уравнению динамики вращательного движения, вращающий момент М, приложенный к диску, равен произведению момента инерции I диска на его угловое ускорение ε: . (4)
. (4) .
. .
.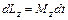 , (1)
, (1)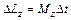 . (2)
. (2)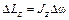 , (3)
, (3) , откуда
, откуда (4)
(4) .
. .
. . (5)
. (5) .
.
 , (1)
, (1)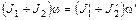 , (2)
, (2)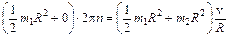 .
. .
.
 .
. .
. передней тележки.
передней тележки.


