
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. О приближенных вычисленияхСодержание книги
Поиск на нашем сайте
Числовые значения физических величин всегда являются приближенными. Это связано с недостаточной точностью измерений. К таким величинам относятся, в частности, многие физические константы. Например, округленные с точность до трех значащих цифр скорость света в вакууме с ≈ 3, 00·108 м/с, элементарный заряд е ≈ 1,60·10 –19 Кл, гравитационная постоянная G ≈ 6,67·10 –11 Н·м2/кг2 и т.д. Более точные значения этих величин с = 2,99792458·108 м/с, е = 1,6021892·10 –19 Кл, G = 6,6720·10 –11 Н·м2/кг2. Однако, и эти значения являются, в свою очередь, приближенными. Поэтому, приступая к вычислениям, необходимо помнить о той точности, которую нужно получить. Одна из самых распространенных ошибок состоит в том, что при вычислениях добиваются получения такой точности результатов, которая совершенно не соответствует точности данных задачи. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают этого. При вычислениях определяют количество верных значащих цифр в числе. При подсчете значащих цифр не считаются нули с левой стороны. Нули в середине или в конце числа (справа), обозначающие отсутствие в числе единиц соответствующих разрядов, – значащие цифры. Например, в числе 0,08040 первые два нуля – не значащие, а третий и четвертый – значащие. Приближенные числа следует записывать, сохраняя только верные знаки. Нули, поставленные в конце целого числа взамен неизвестных цифр и служащие только для определения разрядов остальных цифр, значащими не считаются. В подобных случаях нули в конце числа не пишут, заменяя их соответствующей степенью числа 10. Например, если число 52 400 измерено с абсолютной погрешностью Если приближенной число содержит лишние цифры, то его округляют. При этом руководствуются следующими правилами округления. 1. Если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 27,3763 до сотых, следует записать 27,38. 2. Если первая отбрасываемая цифра меньше 4 или равна 4, то последняя сохраняемая цифра не изменяется. Например, округляя число 13 847 до сотен, записывают 138∙102. 3. Если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например, при округлении до десятых 23,65 ≈ 23,6, но 23,75 ≈ 23,8. Производя вычисления, руководствуются следующими правилами подсчета цифр. 1. При сложении и вычитании в результате сохраняют столько д е с я т и ч н ы х з н а к о в, сколько их содержится в числе с наименьшим количеством десятичных знаков. 2. При умножении и делении в результате сохраняют столько з н а ч а щ и х ц и ф р, сколько их имеет приближенное число с наименьшим количеством значащих цифр. 3. При возведении в квадрат и куб в результате следует сохранять столько з н а ч а щ и х ц и ф р, сколько их имеет возводимое в степень число. 4. При извлечении квадратного и кубического корней в результате следует брать столько з н а ч а щ и х ц и ф р, сколько их имеет подкоренное число.
При вычислении промежуточных результатов сохраняют на одну цифру больше, чем указано в правилах 1. – 4. (так называемая запасная цифра). В окончательном результате запасная цифра отбрасывается. Если некоторые числа содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно округляют, сохраняя только одну лишнюю цифру. В окончательном результате запасная цифра отбрасывается. Пример 1. При сложении чисел 0,2372 + 5,368 + 43,2 = 48,8052 первое и второе нужно округлить до сотых, а в окончательном результате сотые отбросить: 0,24 + 5,37 + 43,2 ≈ 48,8. Сумма округлена до десятых долей, так как слагаемое 43,2 задано с точностью до десятых долей. Пример 2. Требуется вычислить 10,6 × 2,456 × 5,1846. Предварительно округляем и вычисляем выражение 10,6 × 2,46 × 5,18 = 135,07368» 135. В результате оставлено три значащих цифры. Пример 3. При возведении в куб числа 216 результат должен быть записан только с тремя значащими цифрами: 2163 ≈ 101∙105. Пример 4. При извлечении корня в результате сохранено три значащих цифры:
Пример 5.
Сомножитель 5,1 имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр:
После округления результата до двух значащих цифр, получаем 3,8.103.
[1]Количество вещества – число структурных элементов (молекул, атомов, ионов и т. п.), содержащихся в теле или системе. Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.006 с.) |

 100, то это число должно быть записано в виде или 5,24∙104. Такая запись подчеркивает, что в данном числе содержатся лишь три значащие цифры.
100, то это число должно быть записано в виде или 5,24∙104. Такая запись подчеркивает, что в данном числе содержатся лишь три значащие цифры. .
.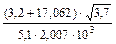 .
.



