
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярная физика и термодинамикаСодержание книги
Поиск на нашем сайте
Основные законы и формулы Молекулярно-кинетическая теория идеальных газов · Количество вещества[1] тела (системы)
где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело; NA.– постоянная Авогадро (N A = 6,02·1023 моль-1). · Молярная масса вещества (масса 1 моля вещества)
где m –масса однородного тела (системы); n – количество вещества этого тела. · Относительная молекулярная масса вещества
где ni - число атомов i -го химического элемента, входящих в состав молекулы данного вещества; Ar,i – относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева. · Молярная масса, выраженная в граммах на моль, численно равна относительной молекулярной массе
где k = 10–3 кг/моль. · Уравнение состояния идеального газа (уравнение Клапейрона – Менделеева)
где т – масса газа, М – молярная масса газа, R – молярная газовая постоянная, n – количество вещества, Т – термодинамическая температура. · Опытные газовые законы, являющиеся частными случаями уравнения Менделеева – Клапейрона для изопроцессов: а) закон Бойля – Мариотта (изотермический процесс:
б) закон Гей-Люссака (изобарный процесс:
в) закон Шарля (изохорный процесс:
где p 1, V 1, T 1 – давление, объем и температура газа в начальном состоянии; p 2, V 2, T 2 – те же величины в конечном состоянии. · Концентрация молекул однородной системы
где N – число молекул, содержащихся в данной системе; ρ – плотность вещества в любом агрегатном состоянии; V – объем системы. · Зависимость давления газа от концентрации молекул и температуры
где k = R / N A = 1,38×10 –23 Дж/К – постоянная Больцмана. · Основное уравнение молекулярно-кинетической теории газов p = или p = где<vкв > – средняя квадратичная скорость молекул, Е – суммарная кинетическая энергия поступательного движения всех молекул газа, m 0 – масса одной молекулы. · Средняя кинетическая энергия молекулы с учетом поступательного и вращательного движения. Вклад в энергию колебательного движения учитывается только при температурах порядка нескольких тысяч кельвинов.
где i – сумма числа поступательных и вращательных степеней свободы молекулы; i = 3 для одноатомной молекулы, i = 5 для двухатомной и i = 6 для трех- и более атомной молекулы. · Средняя кинетическая энергия: поступательного движения молекулы (i п = 3)
вращательного движения молекулы
где i вр – число вращательных степеней свободы (i вр = 2 для двухатомной и i вр = 3 для трех- и более атомной молекулы). · Скорости газовых молекул: средняя квадратичная
средняя арифметическая
наиболее вероятная
где m 0 – масса одной молекулы. · Барометрическая формула p(h) = p 0 exp –(Mgh / RT), где p(h)– давление атмосферы на высоте h от поверхности Земли, p 0 – давление на поверхности (h = 0). · Среднее число соударений, испытываемых одной молекулой газa в единицу времени,
где d – эффективный диаметр молекулы; n – концентрация молекул; < v > – средняя арифметическая скорость молекул. · Средняя длина свободного пробега молекул газа
Основы термодинамики · Внутренняя энергия идеального газа
· Первое начало термодинамики
где Q –количество теплоты, сообщенное системе (газу); ∆U –изменение ее внутренней энергии; А – работа системы против внешних сил. · Связь между удельной с и молярной С теплоемкостями
· Молярные теплоемкости газа при постоянном объеме (
· Уравнение Майера
· Работа расширения газа: в общем случае при изобарном процессе при изотермическом процессе · Уравнения адиабатного процесса (уравнение Пуассона) · · Связь между начальными и конечными значениями параметров идеального газа при адиабатном процессе
где · Работа при адиабатном процессе
· Tермический КПД цикла
где Q 1 – количество теплоты, полученное рабочим телом от нагревателя; Q 2 – количество теплоты, отданное рабочим телом холодильнику, А – работа, совершаемая за цикл. · Термический КПД цикла Карно
гдe Т 1 и Т 2 – температуры нагревателя и холодильника. · Изменение энтропии при равновесном переходе из состояния А в состояние В
2.3. Свойства жидкостей
· Поверхностное натяжение
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; ∆ Е – поверхностная энергия, связанная с площадью ∆ S поверхности пленки.
· Формула Лапласа, выражающая избыточное давление Δ р, создаваемое сферической поверхностью жидкости:
где R – радиус сферической поверхности. · Высота подъема жидкости в капиллярной трубке
где θ – краевой угол (θ = 0 при полном смачивании стенок трубки жидкостью); r– радиус канала трубки; ρ – плотность жидкости; g – ускорение свободного падения. · Высота подъема жидкости между двумя близкими параллельными друг другу плоскостями
где d – расстояние между плоскостями. Примеры решения задач Пример 2.1. Определить число N молекул, содержащихся в объеме V = 1 мм 3 воды, и массу т0 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул. Решение. Число N молекул, содержащихся в некоторой системе массой т, равно произведению постоянной Авогадро
где М – молярная масса. Выразив в этой формуле массу как произведение плотности на объем V, получим
Произведем вычисления, учитывая, что M = 18×10–3 кг/моль:
Масса m 0 одной молекулы
Подставив в (1) значения М и
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка)
Объем V 0 найдем, разделив молярный объем Vm на число молекул в моле, т. е. на
Подставим выражение (3) в (2):
Проверим, дает ли правая часть выражения (4) единицу длины:
Произведем вычисления:
Пример 2.2. Чему равны средние кинетические энергии поступательного и вращательного движения всех молекул, содержащихся в m = 2 кг водорода при температуре T = 400 К? Решение: Считаем водород идеальным газом. Молекула водорода – двухатомная, связь между атомами считаем жесткой, т.е. колебательных степеней свободы не учитываем, тогда число степеней свободы молекулы водорода i = 5. В среднем на одну степень свободы приходится энергия Поступательному движению приписывается три (iп =3), а вращательному движению двухатомной молекулы – две (iвр =2) степени свободы. Средние энергии:
Тогда средняя кинетическая энергия поступательного движения всех молекул водорода будет равна:
где Аналогично средняя кинетическая энергия вращательного движения молекул водорода
Подставляя числовые значения в формулы (1) и (2), имеем
Пример 2.3. Определить среднюю длину свободного пробега и среднее число столкновений за 1с молекулы кислорода, находящегося в сосуде емкостью V = 2 л при температуре t = 27˚С и давлении p = 100 кПа. Решение. Средняя длина свободного пробега молекул вычисляется по формуле
где d – эффективный диаметр молекулы кислорода находим из таблиц, d = 0,29 нм; n – число молекул в единице объема, которое можно определить из уравнения р = nkT
Среднее число соударений молекулы за 1с равно
где
Подставляя числовые значения, находим
Пример 2.4. Определить удельные теплоемкости при постоянном объеме cV и при постоянном давлении сP неона и водорода, принимая эти газы за идеальные.
Р ешение. Удельные теплоёмкости идеальных газов выражаются формулами
где i – число степеней свободы молекулы газа, M – молярная масса. Для неона (одноатомный газ) i 1 = 3, М 1 = 20·10–3 кг/моль. Подставив значения i 1, М 1, R и произведя вычисления, найдем: c V1 =624 Дж/(кг·К); cp 1= 1,04 кДж/(кг·К). Для водорода (двухатомный газ) i 2 = 5, M 2 = 2·10––3 кг/моль. Вычисление даёт следующие значения^ c V2 =10,4 кДж/(кг·К); cp 2= 14,6 кДж/(кг·К). Пример 2.5. Кислород массой m = 160 г нагревают при постоянном давлении от Т1 = 320 К до Т2 = 340 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа. Решение: Количество теплоты, необходимое для нагревания газа при постоянном давлении,
Здесь ср и Ср = Мср – удельная и молярная теплоемкости газа при постоянном давлении, М = 32·10–3 кг/моль – молярная масса кислорода. Для всех двухатомных газов Изменение внутренней энергии газа находим по формуле
где С V – молярная теплоемкость газа при постоянном объеме. Для всех двухатомных газов
При изобарном процессе
Вычитая выражения (4) из (3), находим
следовательно,
Подставляя числовые значения в формулы (1), (2) и (5), получаем, Q = 2,91 кДж; Δ U = 2,08 кДж; A = 831 Дж. Пример 2.6. Объем аргона, находящегося при давлении p = 80 кПа, увеличился от V1 = 1 л до V2 = 2 л. На сколько изменится внутренняя энергия газа, если расширение производилось: а) изобарно; б) адиабатно? Решение: Изменение внутренней энергии
зависит от характера процесса, при котором идет расширение газа. Найти Δ U по формуле (1) нельзя, так какмасса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование формулы (1). Запишем уравнение Клапейрона - Менделеева для начального и конечного состояний газа:
или, вычитая уравнения,
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.172.105 (0.012 с.) |

 или
или  ,
, ,
, ,
,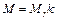 ,
, ,
, )
)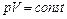 , или для двух состояний газа
, или для двух состояний газа 
 )
) , или для двух состояний
, или для двух состояний 
 )
) , или для двух состояний
, или для двух состояний 
 ,
, ,
, nm 0<vкв>2 или pV =
nm 0<vкв>2 или pV = 

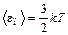 ,
, ,
,
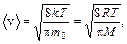

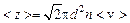 ,
, .
. .
. ,
, .
. ) и постоянном давлении (
) и постоянном давлении ( )
) ,
,  .
. .
. ;
; ;
; .
. .
. ,
,  ,
, 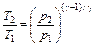 ,
, – показатель адиабаты.
– показатель адиабаты. или
или  .
.

 .
. , или
, или  ,
,


 на количество вещества n:
на количество вещества n: .
.  ,
, .
. .
. . (1)
. (1) .
. , где d – диаметр молекулы. Отсюда
, где d – диаметр молекулы. Отсюда . (2)
. (2) . (3)
. (3) . (4)
. (4) .
. .
. , где k – постоянная Больцмана, Т – термодинамическая температура.
, где k – постоянная Больцмана, Т – термодинамическая температура. ,
,  .
. Число молекул, содержащихся в произвольной массе газа,
Число молекул, содержащихся в произвольной массе газа,  , где
, где  , (1)
, (1) - молярная газовая постоянная.
- молярная газовая постоянная. . (2)
. (2) ,
, .
. ,
, .
. ,
, - средняя арифметическая скорость молекулы
- средняя арифметическая скорость молекулы .
.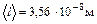 , < z > = 1,25∙1010 с –1.
, < z > = 1,25∙1010 с –1. и
и  ,.
,. . (1)
. (1) ; C р = 29,09 Дж/(моль К).
; C р = 29,09 Дж/(моль К). , (2)
, (2)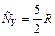 , C V = 20,78 Дж/(моль К).
, C V = 20,78 Дж/(моль К). Работа расширения газа при изобарном процессе
Работа расширения газа при изобарном процессе  , где
, где 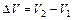 – изменение объема газа, которое можно найти из уравнения Клапейрона – Менделеева.
– изменение объема газа, которое можно найти из уравнения Клапейрона – Менделеева. , (3)
, (3) . (4)
. (4)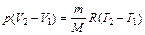 ,
,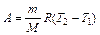 . (5)
. (5) (1).
(1). и
и 
 . (2)
. (2)


