
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовые числа, их физический смысл.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Квантовые числа – целые или дробные числа, определяющие возможные значения физических величин, характеризующих квантовую систему (молекулу, атом, атомное ядро, элементарную частицу). Квантовые числа отражают дискретность (квантованность) физических величин, характеризующих микросистему. Набор квантовых чисел, исчерпывающе описывающих микросистему, называют полным. Так состояние электрона в атоме водорода определяется четырьмя квантовыми числами: главным квантовым числом n (может принимать значения 1, 2, 3, …), определяющим энергию Еn электрона (Еn = -13.6/n2 эВ); орбитальным квантовым числом l = 0, 1, 2, …, n – 1, определяющим величину L орбитального момента количества движения электрона (L = [l(l + 1)]1/2); магнитным квантовым числом m < ± l, определяющим направление вектора орбитального момента; и квантовым числом ms = ± 1/2, определяющим направление вектора спина электрона. n Главное квантовое число: n = 1, 2, …. j Квантовое число полного углового момента. j никогда не бывает отрицательным и может быть целым (включая ноль) или полуцелым в зависимости от свойств рассматриваемой системы. Величина полного углового момента J связана с j соотношением J2 = 2j(j + 1). = +, где и векторы орбитального и спинового угловых моментов. l Квантовое число орбитального углового момента l может принимать только целые значения: l = 0, 1, 2, …. Величина орбитального углового L момента связана с l соотношением L2 = 2l(l + 1).
m Магнитное квантовое число. Проекция полного, орбитального или спинового углового момента на выделенную ось (обычно ось z) равна m. Для полного момента mj = j, j-1, j-2, …, - (j-1), - j. Для орбитального момента ml = l, l-1, l-2, …, -(l-1), -l. Для спинового момента электрона, протона, нейтрона, кварка ms = ±1/2 s Квантовое число спинового углового момента s может быть либо целым, либо полуцелым. s - неизменная характеристика частицы, определяемая ее свойствами. Величина спинового момента S связана с s соотношением S2 = 2s(s + 1). P Пространственная четность. Она равна либо +1, либо -1 и характеризует поведение системы при зеркальном отражении. P = (-1)l. 28 Гармонический осциллятор в квантовой механике
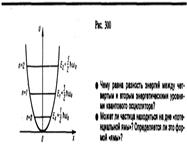
Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что уравнение (222.2) решается только при собственных значениях энергии ) Формула (222.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным значением энергии E 0=1/2ћw0 . Существование минимальной энергии — она называется энергией нулевых колебаний — является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей. Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме». Вывод о наличии энергии нулевых колебаний квантового осциллятора противоречит выводам классической теории, согласно которой наименьшая энергия, которую может иметь осциллятор, равна нулю (соответствует покоящейся в положении равновесия частице). Например, классическая физика приводит к выводу, что при Т =0 энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное колебаниями атомов. Однако эксперимент показывает, что интенсивность рассеяния света при понижении температуры не равна нулю, а стремится к некоторому предельному значению, указывающему на то, что при Т ®0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний. Из формулы (222.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга, а именно расстояние между соседними энергетическими уровнями равно ћ w0, причем минимальное значение энергии E 0=1/2 ћ w0. Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию от классического рассмотрения. Квантовомеханический расчет показывает, что частицу можно обнаружить за пределами дозволенной области | x| £ x max, в то время как с классической точки зрения она не может выйти за пределы области (– x max, + x max). Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без его вывода) демонстрируется на рис. 301, где приводится квантовая плотность вероятности w обнаружения осциллятора для состояния п =1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности w имеет конечные значения за пределами классически дозволенной области | x| £ x max, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу в области за пределами «потенциальной ямы». Существование отличных от нуля значений w за пределами «потенциальной ямы» объясняется возможностью прохождения микрочастиц сквозь потенциальный барьер. 31. Неразличимость частиц квантовой механики.Принцип Паули.Бозоны и фермионы. Взаимодействие - следствие существования у частиц особого свойства, называемого зарядом. Когда заряд равен нулю, то, казалось бы, взаимодействия нет. Но квантовая механика вносит свои коррективы. При равенстве соответствующего заряда нулю сила притяжения или отталкивания, обязанная ему, действительно равна нулю. Но взаимодействие все же есть. Оно проявляется в том, что состояние двух одинаковых частиц не есть произвольное состояние каждой из частиц. Состояние должно удовлетворять принципу неразличимости. В квантовой механике у частицы нет определенной траектории. Возможны квантовые скачки, можно с определенной вероятностью обнаружить частицу на первый взгляд в неожиданном месте - непрерывно следить за ней невозможно. Свою неразличимость частицы проявляют по-разному. Как именно, зависит от их спина - целый он (в частности, нулевой) или полуцелый. Если частицы - бозоны, то есть имеют нулевой или целый спин, то функция, описывающая состояние двух частиц, при перестановке частиц местами вовсе не меняется. Если же частицы - фермионы с полуцелым спином, функция, описывающая состояние двух частиц, при перестановке частиц меняет знак. (В квантовой теории перемена частиц местами - чисто математическая процедура: в функции, описывающей их состояние, меняют местами аргументы, относящиеся к разным частицам). Это различие кардинально влияет на поведение совокупностей квантовых частиц - как принято говорить, на их статистику. О различии статистик можно сказать совсем кратко: любому количеству бозонов ничто не мешает скапливаться в одном состоянии. Именно это их свойство позволило получить "пятое состояние вещества" - так называемый бозе-эйнштейновский конденсат, когерентную материю, комок атомов в одном квантовом состоянии. А число фермионов в каждом состоянии либо 0, либо 1. Третьего не дано! Для фермионов осуществляется запрет: две одинаковые частицы не могут находиться в одном и том же состоянии. Этот запрет в 1924 году впервые сформулировал Вольфганг Паули (1900-1958). Запрет заслуженно называется принципом Паули. Состояние электрона в любом атоме определяют четыре числа: главное квантовое число n (n = 1,2,3…); орбитальный момент количества движения l Ј (n - 1); проекция момента на ось квантования lz (таких проекций 2l +1); проекция спина на ось квантования (их две - либо +1/2, либо -1/2).Принцип Паули запрещает электронам иметь четыре совпадающие характеристики. Этот запрет диктует закон, по которому построена электронная оболочка атома. 32. Распределения атомов по состоянию. Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули). Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется. Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел: главного n (n=1, 2, 3,...), орбитального l (l =0, 1, 2,..., n-1), магнитного ml (ml= - l,..., -1, 0, + 1,..., +l), магнитного спинового ms (ms=+ 1/2, -1/2). Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, l, ml и ms, т. е. Z (n, l, ml, ms)=0 или 1, где Z (n, l, ml, ms) — число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: n, l, ml, ms. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа. Согласно формуле (223.8), данному n соответствует n2 различных состояний, отличающихся значениями l и ml. Квантовое число ms может принимать лишь два значения (±1/2). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n- 1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l+1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 6.
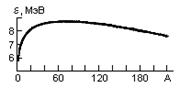
33. Периодическая система. Периодическую систему элементов Д. И. Менделеева (1869) — фундаментального закона природы, являющегося основой современной химии, атомной и ядерной физики, можно объяснить по принципу Паули. Д. И. Менделеев ввел понятие порядкового номера Z химического элемента, равного числу протонов в ядре и соответственно общему числу электронов в электронной оболочке атома. Расположив химические элементы по мере возрастания порядковых номеров, он получил периодичность в изменении химических свойств элементов. Однако для известных в то время 64 химических элементов некоторые клетки таблицы оказались незаполненными, так как соответствующие им элементы (например, Ga, Se, Ge) тогда еще не были известны. Д. И. Менделеев, таким образом, не только правильно расположил известные элементы, но и предсказал существование новых, еще не открытых, элементов и их основные свойства. Кроме того, Д. И. Менделееву удалось уточнить атомные веса некоторых элементов. Например, атомные веса Be и U, вычисленные на основе таблицы Менделеева, оказались правильными, а полученные ранее экспериментально — ошибочными. Так как химические и некоторые физические свойства элементов объясняются внешними (валентными) электронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах. Поэтому для объяснения таблицы будем считать, что каждый последующий элемент образован из предыдущего прибавлением к ядру одного протона и соответственно прибавлением одного электрона в электронной оболочке атома. Взаимодействием электронов пренебрегаем, внося, где это необходимо, соответствующие поправки. Рассмотрим атомы химических элементов, находящиеся в основном состоянии. Единственный электрон атома водорода находится в состоянии 1s, характеризуемом квантовыми числами n= 1, l= 0, ml =0и ms=±1/2 (ориентация его спина произвольна). Оба электрона атома Не находятся в состоянии 1s, но с антипараллельной ориентацией спина. Электронная конфигурация для атома Не записывается как 1s2 (два 1s-электрона). На атоме Не заканчивается заполнение K-оболочки, что соответствует завершению I периода. Третий электрон атома Li (Z=3), согласно принципу Паули, уже не может разместиться в целиком заполненной K-оболочке и занимает наинизшее энергетическое состояние с n=2 (L-оболочка), т. е. 2s-состояние. Электронная конфигурация для атома Li: 1s22s. Атомом Li начинается II период Периодической системы элементов. Четвертым электроном Be (Z=4) заканчивается заполнение подоболочки 2s. У следующих шести элементов от В (Z=5) до Ne (Z=10) идет заполнение подоболочки 2р (табл. 7). II период Периодической системы заканчивается неоном — инертным газом, для которого под-оболочка 2р полностью заполнена. Таким образом, открытая Менделеевым периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов. Так, инертные газы имеют одинаковые внешние оболочки из 8 электронов (заполненные s- и р-состояния); во внешней оболочке щелочных металлов (Li, Na, К, Rb, Cs, Fr) имеется лишь один s-электрон; во внешней оболочке щелочноземельных металлов (Be, Mg, Ca, Sr, Ba, Ra) имеется два s-электрона; галоиды (F, Cl, Br, I, At) имеют внешние оболочки, в которых недостает одного электрона до оболочки инертного газа, и т. д. 34. Строение атомных ядер. Атомное ядро состоит из элементарных частиц — протонов и нейтронов. Протон (р) имеет положительный заряд, равный заряду электрона, и массу покоя mp=1,6726•10-27 кг»1836me, где me — масса электрона. Нейтрон (n) — нейтральная частица с массой покоя mn=1,6749•10-27кг»1839me,. Протоны и нейтроны называются нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом Ze, где е — заряд протона, Z — зарядовое число ядра, равное числу протонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева. Известные в настоящее время 107 элементов таблицы Менделеева имеют зарядовые числа ядер от Z=1 до Z=107. Ядро обозначается тем же символом, что и нейтральный атом: AZХ, где X — символ химического элемента, Z — атомный номер (число протонов в ядре), А — массовое число (число нуклонов в ядре). Сейчас протонно-нейтронная модель ядра не вызывает сомнений. Рассматривалась также гипотеза о протонно-электронном строении ядра, но она не выдержала экспериментальной проверки. Так, если придерживаться этой гипотезы, то массовое число А должно представлять собой число протонов в ядре, а разность между массовым числом и числом электронов должна быть равна заряду ядра. Эта модель согласовывалась со значениями изотопных масс и зарядов, но противоречила значениям спинов и магнитных моментов ядер, энергии связи ядра и т. д. Кроме того, она оказалась несовместимой с соотношением неопределенностей (см. §215). В результате гипотеза о протонно-электронном строении ядра была отвергнута. 35. Масса и энергия связи ядра. Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С: 1а.е.м = 1.6606 10-27 кг. А.е.м. выражается через энергетические единицы: 1а.е.м = 1.510-3 эрг = 1.510-10Дж = 931.49 МэВ Масса ядра всегда меньше суммы масс составляющих его нуклонов. Энергия связи ядра Eсв(A,Z) это минимальная энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны. Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)]c2, где Z - число протонов, (A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z. Энергия связи ядра, выраженная через массу атома Mат, имеет вид: Есв(A, Z) = [ZmH + (A - Z)mn - Mат(A, Z)]c2, где mH - масса атома водорода. Удельная энергия связи ядра ε(A, Z) это энергия связи, приходящаяся на один нуклон ε(A, Z) = Eсв(A,Z) / A. На рис. 1 показана зависимость удельной энергии связи ядра ε от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых - деление на более легкие осколки. Избыток масс Δ связан с массой атома Mат(A,Z) и массовым числом A соотношением:
Δ = Мат(A,Z) - А.
Наиболее устойчивы ядра, у которых магическое число протонов или нейтронов.
36. Взаимодействие нуклонов в ядре. Природа ядерных сил. Си́льное ядерное взаимоде́йствие (цветово́е взаимоде́йствие, я́дерное взаимоде́йствие) — одно из четырёх фундаментальных взаимодействий в физике. В сильном взаимодействии участвуют кварки и глюоны и составленные из них частицы, называемые адронами (барионы и мезоны). Оно действует в масштабах порядка размера атомного ядра и менее, отвечая за связь между кварками в адронах и за притяжение между нуклонами (разновидность барионов — протоны и нейтроны) в ядрах. На расстояниях порядка
в котором константа сильного взаимодействия, обычно полагающаяся равной в «системе констант» фундаментальных взаимодействий, где, например, постоянная электромагнитного взаимодействия равна постоянной тонкой структуры (Такая потенциальная функция называется потенциалом Юкавы.) Модуль этой функции очень быстро убывает и на расстояниях, больших уже ничтожно мал. Вообще радиус ядра можно определить по приближенной формуле
Свойства ядерных сил, их описание и происхождение 1.Ядерные силы - это силы притяжения, так как они удерживают нуклоны внутри ядра (при очень сильном сближении нуклонов ядерные силы между ними имеют характер отталкивания). 2.Ядерные силы – это не электрические силы, так как они действуют не только между протонами, но и между не имеющими зарядов нейтронами, и не гравитационные, которые слишком малы для объяснения ядерных эффектов. 3.Область действия ядерных сил, ничтожно мала. Радиус их действия 10-13. При больших расстояниях между частицами ядерное взаимодействие не проявляется. 4.Ядерные силы (в той области, где они действуют) очень интенсивные. Их интенсивность значительно больше интенсивности электромагнитных сил, так как ядерные силы удерживают внутри ядра, одноимённо заряженные протоны, отталкивающиеся друг от друга с огромными электрическими силами. 5.Изучение степени связанности нуклонов в разных ядрах показывают, что ядерные силы обладают свойством насыщения, аналогичным валентности химических сил. В соответствии с этим свойством ядерных сил один и тот же нуклон взаимодействует не со всеми остальными нуклонами ядра. А только с несколькими соседними. 6.Важнейшим свойством ядерных сил является их зарядовая независимость, то есть тождественность трёх типов ядерного взаимодействия: между двумя протонами, между протоном и нейтроном и между двумя нейтронами.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3008; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.013 с.) |



 Наиболее устойчивы ядра, у которых магическое число протонов или нейтронов.
Наиболее устойчивы ядра, у которых магическое число протонов или нейтронов.
 м величина сильного взаимодействия между нуклонами, составляющими атомное ядро, настолько велика, что позволяет практически не принимать во внимание их электромагнитное взаимодействие (отталкивание). Вообще говоря, взаимодействие нуклонов в ядре не является «элементарным»; скорее оно является таким же неизбежным следствием наличия сильного взаимодействия между частицами, например, составляющими нуклон кварками, как силы Ван-дер-Ваальса — следствием существования электромагнетизма. В хорошем приближении потенциальная функция взаимодействия двух нуклонов описывается выражением
м величина сильного взаимодействия между нуклонами, составляющими атомное ядро, настолько велика, что позволяет практически не принимать во внимание их электромагнитное взаимодействие (отталкивание). Вообще говоря, взаимодействие нуклонов в ядре не является «элементарным»; скорее оно является таким же неизбежным следствием наличия сильного взаимодействия между частицами, например, составляющими нуклон кварками, как силы Ван-дер-Ваальса — следствием существования электромагнетизма. В хорошем приближении потенциальная функция взаимодействия двух нуклонов описывается выражением
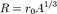 где А общее число нуклонов в ядре. Отсюда можно, в частности, очень приближённо найти массу мезона как переносчика сильного взаимодействия (впервые это было сделано японским физиком Хидэки Юкавой). Для этого, однако, придётся сделать пару предположений, которые при строгом рассмотрении могут показаться безосновательными. Предположим, что мезон испускается одним нуклоном, и, совершив один «оборот» по «краю» потенциальной ямы (первое такое предположение), поглощается другим. Максимальная и, значит, наиболее вероятная длина волны его при этом
где А общее число нуклонов в ядре. Отсюда можно, в частности, очень приближённо найти массу мезона как переносчика сильного взаимодействия (впервые это было сделано японским физиком Хидэки Юкавой). Для этого, однако, придётся сделать пару предположений, которые при строгом рассмотрении могут показаться безосновательными. Предположим, что мезон испускается одним нуклоном, и, совершив один «оборот» по «краю» потенциальной ямы (первое такое предположение), поглощается другим. Максимальная и, значит, наиболее вероятная длина волны его при этом 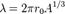 Импульс мезона
Импульс мезона  .
.




