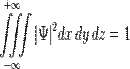Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поглощение света. Закон Бугера.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Дифракция от щели. Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, например, в близи границ прозрачных или непрозрачных тел, сквозь малые отверстия. Дифракция, в частности, приводит к огибанию световыми волнами препятствий, и проникновению света в область геометрической тени. Бесконечно длинную щель можно образовать, расположив ряжом две обращенные в разные стороны полуплоскости. Следовательно, задача и дифракции Френеля от щели может быть решена с помощью спирали Карню. Волновую пов-ть падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу. Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку Р’, лежащую против края щели, начало результирующего вектора переместится в середину спирали О.
Конец вектора переместится по спирали в направлении полюса F1. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (вектор, соответствующий точке Р’’).
Интенсивность света при этом достигнет минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки Р в противоположное сторону, так как дифракционная картина симметрична относительно середины щели.
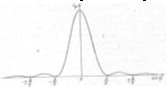
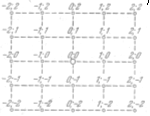
Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (а) и отличные от нуля минимумы (б). 8. Дифракционная решетка и дифракционные спектры. Дифракционной решеткой называется последовательность из большого числа N одинаковых параллельных щелей. Ширина каждой щели равна b, расстояние между соседними щелями, которое называется периодом
решетки, равно d. Расположим параллельно решетке собирательную линзу, в фокальной пл-ти которой поставим экран. Выясним характер диф. картины, получающейся на экране при падении на решетку световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на экране картину, описываемую кривой, изобр на рис. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку Р от различных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью лишь тем, что все интенсивности выросли бы в N раз.
Однако, колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от Дифракционный спектр – Распределение интенсивности на экране, получаемое вследствие дифракции (это явление приведено на нижнем рис.). Основная часть световой энергии сосредоточена в центральном максимуме. Сужение щели приводит к тому, что центральный максимум расплывается, а его яркость уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире ( 9. Дифракция рентгеновских волн. Это не видимые глазом эл. магн. излучение м длиной волны
В итоге дифракционная картина будет иметь вид правильно расположенных пятен, каждому из которых соответствуют два целочисленных индекса 10.Дисперсия света (разложение света) - это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней: у красного цвета максимальная скорость в среде и минимальная степень преломления, у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления. Дисперсия света.
ν(в)=(n2-n1)/(λ2-λ1)=∆n/∆λ; ∆λà0, ν=dn/dλ. Для большинства прозрачных сред n монотонно убывает с увеличением длины волны. Из графиков следует, что n наиболее резко изменяется в области коротких длин волн => DB резко изменяется в области коротких длин волн. n=f(λ)=A+B/λ(c.2), где A и B – const, характеризующие природу вещества, ν= - 2B/λ(c.3). ПОЛЯРИЗАЦИЯ СВЕТА одно из фундаментальных свойств оптического излучения (света), состоящее в неравноправии различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны). П. с. наз. также геометрич. характеристики, к-рые отражают особенности этого неравноправия. Закон Малюса для поляризованного света. Интенсивность прошедшего света равна интенсивности падающего света на угол между плоскостью колебаний падающего света и плоскостью поляризатора. Поставим на пути естественного света два поляризатора, плоскости которых составляют угол Максимальная интенсивность, равная
14. Поляризацмя света при отражении. Закон Брюстера. Опыт показывает, что при падении на диэлектрик (вода, стекло) отраженный и преломленный лучи всегда частично поляризованы. Степень поляризации при этом зависит от угла падения и показателя преломления отражающей среды. При этом отраженный луч частично поляризован в плоскости, перпендикулярной плоскости падения, а преломленный - в плоскости падения. Условие полной поляризации состоит в том, чтобы угол между отраженным и преломленным лучами был равен π/2, т.е. чтобы n=sin i0/sin r= sin i0/cos i0=tg i0. Это соотношение называют законом Брюстера. Этот закон объясняется тем, что отраженный преломленный лучи представляют собой вторичное излучение, возбужденное падающей волной. Электроны колеблются в направлении вектора Е. Однако электрический диполь не излучает в этом направлении, максимум излучения приходится на перпендикулярное направление Законы излучения абсолютно твердого тела. Противоречивость классической физики. Квантовая физика Планка
Абсолютно черное тело.
Квантовая теория Планка. Формула Планка. Квантовая гипотеза Макса Планка состояла в том, что любая энергия поглощается или испускается только дискретными порциями, которые состоят из целого числа квантов с энергией ε таких, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле:
где h — постоянная Планка. Планку удалось найти аналитический вид функции r (инд. λТ) (в), в точности соответствующий экспериментаьной кривой. Окончательный вид формулы Планка:
Эффект Комптона. Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытиеНобелевскую премию по физике.
При рассеянии фотона на покоящемся электроне частоты фотона
где Перейдя к длинам волн:
где Для электрона Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волнаявляется непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.
Постулаты Бора Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн. Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам для которых момент импульса квантуется: При переходе электрона с орбиты (энергетический уровень) на орбиту излучается или поглощается квант энергии h ν = En − Em, где En; Em — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.
22 Теория Бора для водородоподобных сил
Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты Rn и энергии En находящегося на этой орбите электрона:
Здесь me — масса электрона, Z — количество протонов в ядре, ε0 — диэлектрическая постоянная, e — заряд электрона. Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера, решая задачу о движении электрона в центральном кулоновском поле.Радиус первой орбиты в атоме водорода R0=5,2917720859(36)×10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты E 0 = − 13.6 эВ представляет собой энергию ионизации атома водорода. 23 Гипотеза де Бройля. Дифракция электронов. В 1924г Луи де-Бройль высказал гипотезу, согласно которой дуализм (двойственность) св-в присущи не только оптическим явлениям, но и к материи вообще. В частности с потоком электронов связан волновой процесс, который влияет на поведение электрона как частицу, заряд и масса которой локализованы в малом объеме пространства так, что ведет себя как точечный заряд. Д-Бройль показал, как можно определить длинну электронной волны по аналогии с длинной волны фотона. Pф=m(индекс ф)c=hνc/c (c.2)=hν/c=h/λ; λ(инд.c)=h/P(индекс е)= =h/m(инд. с) v(инд.с) (1). Длина волны, определяемая (1) называется дебройлевой длиной волны. Д-Бройль попробовал объяснить 1-й постулат Бора – постулат квантования. Согласно д-Бройлю, стационарными являются такие орбиты электрона, у которых вдоль периметра укладывается целое число волн д-Бройля. Т.е. вдоль орбиты устанавливается стоячая волна. 2πr = nλ(индекс с), 2π r = nh/mv; mvr = nh/2π=nh(в). Джемер и Дэвисон впервые обнаружили дифракцию электронов при рассеянии их на монохроматические никеля. Электроны, ускоренные разностью потенциалов U, вылетали из эл. пушки в виде узкого пучка, и фокусировались на клисталлической пластинке. Рассеяные электроны улавливались ловушкой цилиндра Фарадея, соединенного с чувствительным гальванометром. Электроны отдавали свой заряд ловушке и устанавливалась зависимость J от √U. Сила тока J является мерой отраженных от пластины электронов, а √U – мера их скорости. mv 2/2=eU; √U~v. Т.о. от кристалла отражаются лишь электроны определенных скоростей. Кристалл представляет собо пространственную дифракционную решетку, в которой источники вторичных волн, т.е. частицы в узлах кристаллической решетки, находятся на строго определенных расстояниях вдоль координатных осей. При прохождении через кристалл электро-магнитного излучения, частицы в узлах кристаллической решетки испускают вторичные волны, которые, налагаясь, образуют максимум и минимум дифракции. То, что от кристалла отражались лишь электроны определенных скоростей означало, что на кристалл падает излучение, представляющее собой волновой процесс, в его избирательное отражение есть результат дифракции.
24. Соотношение неопределенностей Гейзенберга. Во всех макроскопических системах электрон ведет себя как частица, локализованная в малом объеме, обладающая определенной координатой и скоростью. При движении электрона в атоме проявляются его волновые свойства в большей степени, как и во всех микроскопических частицах, но волна не локализована в пространстве, а безгранична. Пусть электроны движутся в направлении ОА со скоростью Vx и встречают узкую щель ВС с шириной а. DE – экран, на который будут попадать электроны. Т.к. электроны обладают волновыми свойствами, то при прохождении через узкую щель они дифрагируют, в результате чего электроны будут попадать не только в точки экрана DE, расположенные непосредственно за щелью, но распределяется по всему экрану. Представим, что электрон – классическая частица. Она характеризуется координатой и количеством движения. Можно охарактеризовать координату электрона в момент прохождения щели как координату щели. В таком определении координаты, однако, есть неточность, обусловленная шириной щели. Обозначим эту неопределенность через ∆x=a. После прохождения щели составляющая импульса Px≠0, т.к. вследствии дифракции изменяется скоростью. Составляющая импульса электрона не может быть определено точно, а лишь с некоторой погрешностью ∆Px≥Psinφ1=Pλ/a=hλ/λa=h/a; ∆Px*∆x≥h (1) – соотношение неопределенностей Гейзенберга. 25.Квантовое состояние. Уравнения Шредингера В квантовой физике вводится комплекснозначная функция Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами
где
[править]Случай трёхмерного пространства В трёхмерном случае пси-функция является функцией трёх координат и
тогда уравнение Шрёдингера примет вид:
где [править]Стационарное уравнение Шрёдингера Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда
где функция
которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции Важное значение имеет интерпретация величины
26 Волновая функция и её статические свойства. Суперпозиция состояний Волнова́я фу́нкция, или пси-функция
где Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями
Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией В таком состоянии квадрат модуля коэффициента Поэтому для нормированных волновых функций
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значенияволновой функции этого состояния в координатном представлении.
Волновая функция
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении. Цепная реакция Цепна́я я́дерная реа́кция — последовательность единичных ядерных реакций, каждая из которых вызывается частицей, появившейся как продукт реакции на предыдущем шаге последовательности. Примером цепной ядерной реакции является цепная реакция деления ядер тяжёлых элементов, при которой основное число актов деления инициируется нейтронами, полученными при делении ядер в предыдущем поколении. Механизм энерговыделения
Превращение вещества сопровождается выделением свободной энергии лишь в том случае, если вещество обладает запасом энергий. Последнее означает, что микрочастицы вещества находятся в состоянии с энергией покоя большей, чем в другом возможном, переход в которое существует. Самопроизвольному переходу всегда препятствует энергетический барьер, для преодоления которого микрочастица должна получить извне какое-то количество энергии — энергии возбуждения. Экзоэнергетическая реакция состоит в том, что в следующем за возбуждением превращении выделяется энергии больше, чем требуется для возбуждения процесса. Существуют два способа преодоления энергетического барьера: либо за счёт кинетической энергии сталкивающихся частиц, либо за счёт энергии связи присоединяющейся частицы.
Если иметь в виду макроскопические масштабы энерговыделения, то необходимую для возбуждения реакций кинетическую энергию должны иметь все или сначала хотя бы некоторая доля частиц вещества. Это достижимо только при повышении температуры среды до величины, при которой энергия теплового движения приближается к величине энергетического порога, ограничивающего течение процесса. В случае молекулярных превращений, то есть химических реакций, такое повышение обычно составляет сотни кельвинов, в случае же ядерных реакций — это минимум 107 К из-за очень большой высоты кулоновских барьеров сталкивающихся ядер. Тепловое возбуждение ядерных реакций осуществлено на практике только при синтезе самых лёгких ядер, у которых кулоновские барьеры минимальны (термоядерный синтез).
Возбуждение присоединяющимися частицами не требует большой кинетической энергии, и, следовательно, не зависит от температуры среды, поскольку происходит за счет неиспользованных связей, присущих частицам сил притяжения. Но зато для возбуждения реакций необходимы сами частицы. И если опять иметь в виду не отдельный акт реакции, а получение энергии в макроскопических масштабах, то это возможно лишь при возникновении цепной реакции. Последняя же возникает, когда возбуждающие реакцию частицы снова появляются как продукты экзоэнергетической реакции. [править] Цепные реакции
Цепные реакции широко распространены среди химических реакций, где роль частиц с неиспользованными связями выполняют свободные атомы или радикалы. Механизм цепной реакции при ядерных превращениях могут обеспечить нейтроны, не имеющие кулоновского барьера и возбуждающие ядра при поглощении. Появление в среде необходимой частицы вызывает цепь следующих, одна за другой реакций, которая продолжается до обрыва цепи вследствие потери частицы-носителя реакции. Основных причин потерь две: поглощение частицы без испускания вторичной и уход частицы за пределы объёма вещества, поддерживающего цепной процесс. Если в каждом акте реакции появляется только одна частица-носитель, то цепная реакция называется неразветвлённой. Неразветвлённая цепная реакция не может привести к энерговыделению в больших масштабах.
Если в каждом акте реакции или в некоторых звеньях цепи появляется более одной частицы, то возникает разветвленная цепная реакция, ибо одна из вторичных частиц продолжает начатую цепь, а другие дают новые цепи, которые снова ветвятся. Правда, с процессом ветвления конкурируют процессы, приводящие к обрывам цепей, и складывающаяся ситуация порождает специфические для разветвленных цепных реакций предельные или критические явления. Если число обрывов цепей больше, чем число появляющихся новых цепей, то самоподдерживающаяся цепная реакция (СЦР) оказывается невозможной. Даже если её возбудить искусственно, введя в среду какое-то количество необходимых частиц, то, поскольку число цепей в этом случае может только убывать, начавшийся процесс быстро затухает. Если же число образующихся новых цепей превосходит число обрывов, цепная реакция быстро распространяется по всему объёму вещества при появлении хотя бы одной начальной частицы.
Область состояний вещества с развитием цепной самоподдерживающейся реакции отделена от области, где цепная реакция вообще невозможна, критическим состоянием. Критическое состояние характеризуется равенством между числом новых цепей и числом обрывов.
Достижение критического состояния определяется рядом факторов. Деление тяжелого ядра возбуждается одним нейтроном, а в результате акта деления появляется более одного нейтрона (например, для 235U число нейтронов, родившихся в одном акте деления, в среднем равно 2,5). Следовательно, процесс деления может породить разветвленную цепную реакцию, носителями которой будут служить нейтроны. Если скорость потерь нейтронов (захватов без деления, вылетов из реакционного объёма и т. д.) компенсирует скорость размножения нейтронов таким образом, что эффективный коэффициент размножения нейтронов в точности равен единице, то цепная реакция идёт в стационарном режиме. Введение отрицательных обратных связей между эффективным коэффициентом размножения и скоростью энерговыделения позволяет осуществить управляемую цепную реакцию, которая используется, например, в ядерной энергетике. Если коэффициент размножения больше единицы, цепная реакция развивается экспоненциально; неуправляемая цепная реакция деления используется в ядерном оружии. 41. Т ермоядерные реакции Термоядерные реакции, ядерные реакции между лёгкими атомными ядрами, протекающие при очень высоких температурах (порядка 107 К и выше). Высокие температуры, то есть достаточно большие относительные энергии сталкивающихся ядер, необходимы для преодоления электростатического барьера, обусловленного взаимным отталкиванием ядер (как одноимённо заряженных частиц). Без этого невозможно сближение ядер на расстояниепорядка радиуса действия ядерных сил, а следовательно, и &
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.013 с.) |





 (
( -- интенсивность, создаваемая одной щелью). Предполагая, что радиус когерентности (максимальное поперечное направлению распространению волны расст., на котором возможно проявление интерференции) падающей волны намного превышает длину решетки. Так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результир. колеб в точке Р представл. собой сумму N колебаний с одинаковыми ампл.
-- интенсивность, создаваемая одной щелью). Предполагая, что радиус когерентности (максимальное поперечное направлению распространению волны расст., на котором возможно проявление интерференции) падающей волны намного превышает длину решетки. Так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результир. колеб в точке Р представл. собой сумму N колебаний с одинаковыми ампл.  , сдвинутых друг относительно друга по фазе на одну и ту же величину
, сдвинутых друг относительно друга по фазе на одну и ту же величину  . Интенсивность при этих условиях равна:
. Интенсивность при этих условиях равна: 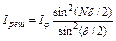 , где
, где  Следов, разность фаз
Следов, разность фаз 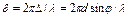
 ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При
), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При 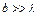 в центре получается резкое изображение источника света, т.е. имеет мет прямолинейное распространение света. Эта картина будет иметь место только для монохроматического света. При освещении щели белым светом, центральный максимум будет иметь место белой полоски, он общий для всех длин волн (при
в центре получается резкое изображение источника света, т.е. имеет мет прямолинейное распространение света. Эта картина будет иметь место только для монохроматического света. При освещении щели белым светом, центральный максимум будет иметь место белой полоски, он общий для всех длин волн (при  разность хода равна нулю для всех
разность хода равна нулю для всех 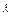 ).
).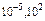 нм. Проникают через некоторые непрозрачные для видимого света материалы, испускаются при быстрых торможениях электронов в вещ-ве и при квантовых переходах электронов с внеш. эл. оболочек атома на внутр. Поставим две дифр. решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка (пусть ее штрихи вертикальны) даст в горизонтальном направлении ряд максимумов, положения которых определяются условием
нм. Проникают через некоторые непрозрачные для видимого света материалы, испускаются при быстрых торможениях электронов в вещ-ве и при квантовых переходах электронов с внеш. эл. оболочек атома на внутр. Поставим две дифр. решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка (пусть ее штрихи вертикальны) даст в горизонтальном направлении ряд максимумов, положения которых определяются условием  Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием:
Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием: 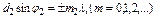 .
.
 и
и  . Такая же диф. картина получается, если вместо двух реальных решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Дифракция так же наблюдается на трехмерных структурах. т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной пл-ти направлениям. Подобными структурами являются все крист тела.Однако их период слишком мал (
. Такая же диф. картина получается, если вместо двух реальных решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Дифракция так же наблюдается на трехмерных структурах. т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной пл-ти направлениям. Подобными структурами являются все крист тела.Однако их период слишком мал ( ), чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие
), чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие  выполняется только для рентгеновских лучей.
выполняется только для рентгеновских лучей. Дисперсия света (ДС) – явление обусловленное зависимостью показателя преломления от длины волны. Для простоты в дальнешем рассмотрим преломление света на границе вакуум-данная среда, т.е. будем рассматривать зависимость абсолютного показателя преломления от длины волны n=f(λ). Дисперсия вещества (ДВ) – физическая величина, показывающая как быстро показатель преломления изменится с изменением длины волны. Если для двух длин волн λ1 и λ2, показатель преломления n1 и n2, то средний дисперсией в этом интервале будет
Дисперсия света (ДС) – явление обусловленное зависимостью показателя преломления от длины волны. Для простоты в дальнешем рассмотрим преломление света на границе вакуум-данная среда, т.е. будем рассматривать зависимость абсолютного показателя преломления от длины волны n=f(λ). Дисперсия вещества (ДВ) – физическая величина, показывающая как быстро показатель преломления изменится с изменением длины волны. Если для двух длин волн λ1 и λ2, показатель преломления n1 и n2, то средний дисперсией в этом интервале будет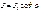 .
. . Из первого поляризатора выйдет плоско-поляризованный свет, интенсивность которого
. Из первого поляризатора выйдет плоско-поляризованный свет, интенсивность которого  . Согласно закону Малюса из второго поляризатора выйдет свет интенсивности
. Согласно закону Малюса из второго поляризатора выйдет свет интенсивности  . Интенсивность света, прошедшего второй поляризатор равна:
. Интенсивность света, прошедшего второй поляризатор равна:  .
. получается при
получается при 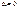 (поляризаторы параллельны). При
(поляризаторы параллельны). При  интенсивность равна нулю (скрещенные поляризаторы света не пропускают).
интенсивность равна нулю (скрещенные поляризаторы света не пропускают). Все твердые тела в природе условно можно разбить на 3 группы: 1) белые тела ρ=1, а=0 (отражают, но не поглощают). 2) абсолютно черные тела ρ=0, a=1 (поглощают, но не отражают), 3) серые тела 0<ρ<1, 0<a<1 (и поглощают и отражают). [ρ = коэффициент отражения, а – коэффициент поглощения]. Абсолютно черных тел (АЧТ) в природе не существует. Приближена – черная сажа (на 99% поглощает), черная фотобумага (на 95% поглощает.
Все твердые тела в природе условно можно разбить на 3 группы: 1) белые тела ρ=1, а=0 (отражают, но не поглощают). 2) абсолютно черные тела ρ=0, a=1 (поглощают, но не отражают), 3) серые тела 0<ρ<1, 0<a<1 (и поглощают и отражают). [ρ = коэффициент отражения, а – коэффициент поглощения]. Абсолютно черных тел (АЧТ) в природе не существует. Приближена – черная сажа (на 99% поглощает), черная фотобумага (на 95% поглощает.

 Иллюстрация к эффекту Комптона
Иллюстрация к эффекту Комптона
 и
и  (до и после рассеяния соответственно) связаны соотношением:
(до и после рассеяния соответственно) связаны соотношением: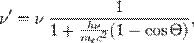
 — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).
— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).
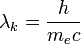 — комптоновская длина волны электрона.
— комптоновская длина волны электрона.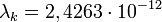 м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.
м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.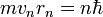 , где n — натуральные числа, а
, где n — натуральные числа, а 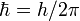 — постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.
— постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.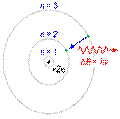 Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома
Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модельатома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]:
Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модельатома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]:  .
.
 , описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.
, описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.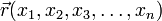 , в определенный момент времени t она будет иметь вид
, в определенный момент времени t она будет иметь вид 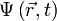 . В таком случае уравнение Шрёдингера запишется в виде:
. В таком случае уравнение Шрёдингера запишется в виде: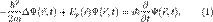
 ,
,  — постоянная Планка;
— постоянная Планка;  — масса частицы,
— масса частицы, 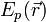 — внешняя по отношению к частице потенциальная энергия в точке
— внешняя по отношению к частице потенциальная энергия в точке  — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид: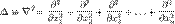
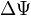 в декартовой системе координат заменяется выражением
в декартовой системе координат заменяется выражением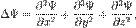

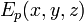 — потенциальная энергия в точке
— потенциальная энергия в точке 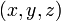
 не является функцией времени, можно записать в виде:
не является функцией времени, можно записать в виде:
 должна удовлетворять уравнению:
должна удовлетворять уравнению:
 от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции
от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции  в уравнении (2). Она производится следующим путём: временна́я зависимость функции
в уравнении (2). Она производится следующим путём: временна́я зависимость функции 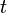 в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель
в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель  умножаетсяна потенциальную энергию
умножаетсяна потенциальную энергию 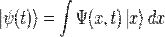
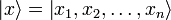 — координатный базисный вектор, а
— координатный базисный вектор, а 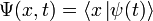 — волновая функция в координатном представлении.
— волновая функция в координатном представлении.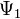 и
и  , то она может пребывать и в состоянии, описываемом волновой функцией
, то она может пребывать и в состоянии, описываемом волновой функцией при любых комплексных
при любых комплексных  и
и  .
.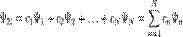 .
. определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией
определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией 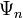 .
. .
.