Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель атома Резерфорда и её недостаткиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Создание Резерфордом планетарной, или ядерной, модели атома было крупным шагом вперед в познании строения атома. Но в некоторых случаях эта теория вступала в противоречие с твердо установленными фактами. Так планетарная модель не могла объяснить устойчивости атома. Вращаясь вокруг ядра, электрон должен часть своей энергии испускать в виде электромагнитных колебаний, что должно привести к нарушению равновесия между электростатическим притяжением электрона к ядру и центробежной силой, обусловленной вращением электрона вокруг ядра. Для восстановления равновесия электрон должен переместиться ближе к ядру. Следовательно, непрерывно излучая электромагнитную энергию, электрон должен постепенно приближаться к ядру и в конце концов упасть на него - существование атома должно прекратиться. В действительности атом очень устойчив и может существовать бесконечно долго.Модель Резерфорда не могла объяснить также характер атомного спектра. Известно, что солнечный свет, проходя через стеклянную призму, образует спектр - цветную полосу, содержащую все цвета радуги.Это явление объясняется тем, что солнечный свет состоит из электромагнитных волн различных частот. Волны различных частот неодинаково преломляются призмой, что приводит к образованию сплошного спектра.Аналогично ведет себя свет, излучаемый раскаленными жидкостями и твердыми телами. Спектр раскаленных газов и паров представляет собой отдельные цветные линии, разделенные темными промежутками, - линейчатый спектр. При этом атомы одного элемента дают вполне определенный спектр, отличающийся от спектра другого элемента.Линейчатый характер спектра водорода не согласуется с теорией Резерфорда, так как излучающий энергию электрон должен приближаться к ядру непрерывно, и его спектр должен быть непрерывным, сплошным.Следовательно, планетарная модель атома не могла объяснить ни устойчивости атомов, ни линейчатый характер спектра газов и паров. Постулаты Бора Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн. Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам для которых момент импульса квантуется: При переходе электрона с орбиты (энергетический уровень) на орбиту излучается или поглощается квант энергии h ν = En − Em, где En; Em — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.
22 Теория Бора для водородоподобных сил
Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты Rn и энергии En находящегося на этой орбите электрона:
Здесь me — масса электрона, Z — количество протонов в ядре, ε0 — диэлектрическая постоянная, e — заряд электрона. Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера, решая задачу о движении электрона в центральном кулоновском поле.Радиус первой орбиты в атоме водорода R0=5,2917720859(36)×10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты E 0 = − 13.6 эВ представляет собой энергию ионизации атома водорода. 23 Гипотеза де Бройля. Дифракция электронов. В 1924г Луи де-Бройль высказал гипотезу, согласно которой дуализм (двойственность) св-в присущи не только оптическим явлениям, но и к материи вообще. В частности с потоком электронов связан волновой процесс, который влияет на поведение электрона как частицу, заряд и масса которой локализованы в малом объеме пространства так, что ведет себя как точечный заряд. Д-Бройль показал, как можно определить длинну электронной волны по аналогии с длинной волны фотона. Pф=m(индекс ф)c=hνc/c (c.2)=hν/c=h/λ; λ(инд.c)=h/P(индекс е)= =h/m(инд. с) v(инд.с) (1). Длина волны, определяемая (1) называется дебройлевой длиной волны. Д-Бройль попробовал объяснить 1-й постулат Бора – постулат квантования. Согласно д-Бройлю, стационарными являются такие орбиты электрона, у которых вдоль периметра укладывается целое число волн д-Бройля. Т.е. вдоль орбиты устанавливается стоячая волна. 2πr = nλ(индекс с), 2π r = nh/mv; mvr = nh/2π=nh(в). Джемер и Дэвисон впервые обнаружили дифракцию электронов при рассеянии их на монохроматические никеля. Электроны, ускоренные разностью потенциалов U, вылетали из эл. пушки в виде узкого пучка, и фокусировались на клисталлической пластинке. Рассеяные электроны улавливались ловушкой цилиндра Фарадея, соединенного с чувствительным гальванометром. Электроны отдавали свой заряд ловушке и устанавливалась зависимость J от √U. Сила тока J является мерой отраженных от пластины электронов, а √U – мера их скорости. mv 2/2=eU; √U~v. Т.о. от кристалла отражаются лишь электроны определенных скоростей. Кристалл представляет собо пространственную дифракционную решетку, в которой источники вторичных волн, т.е. частицы в узлах кристаллической решетки, находятся на строго определенных расстояниях вдоль координатных осей. При прохождении через кристалл электро-магнитного излучения, частицы в узлах кристаллической решетки испускают вторичные волны, которые, налагаясь, образуют максимум и минимум дифракции. То, что от кристалла отражались лишь электроны определенных скоростей означало, что на кристалл падает излучение, представляющее собой волновой процесс, в его избирательное отражение есть результат дифракции.
24. Соотношение неопределенностей Гейзенберга. Во всех макроскопических системах электрон ведет себя как частица, локализованная в малом объеме, обладающая определенной координатой и скоростью. При движении электрона в атоме проявляются его волновые свойства в большей степени, как и во всех микроскопических частицах, но волна не локализована в пространстве, а безгранична. Пусть электроны движутся в направлении ОА со скоростью Vx и встречают узкую щель ВС с шириной а. DE – экран, на который будут попадать электроны. Т.к. электроны обладают волновыми свойствами, то при прохождении через узкую щель они дифрагируют, в результате чего электроны будут попадать не только в точки экрана DE, расположенные непосредственно за щелью, но распределяется по всему экрану. Представим, что электрон – классическая частица. Она характеризуется координатой и количеством движения. Можно охарактеризовать координату электрона в момент прохождения щели как координату щели. В таком определении координаты, однако, есть неточность, обусловленная шириной щели. Обозначим эту неопределенность через ∆x=a. После прохождения щели составляющая импульса Px≠0, т.к. вследствии дифракции изменяется скоростью. Составляющая импульса электрона не может быть определено точно, а лишь с некоторой погрешностью ∆Px≥Psinφ1=Pλ/a=hλ/λa=h/a; ∆Px*∆x≥h (1) – соотношение неопределенностей Гейзенберга. 25.Квантовое состояние. Уравнения Шредингера В квантовой физике вводится комплекснозначная функция Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами
где
[править]Случай трёхмерного пространства В трёхмерном случае пси-функция является функцией трёх координат и
тогда уравнение Шрёдингера примет вид:
где [править]Стационарное уравнение Шрёдингера Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда
где функция
которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции Важное значение имеет интерпретация величины
26 Волновая функция и её статические свойства. Суперпозиция состояний Волнова́я фу́нкция, или пси-функция
где Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями
Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией В таком состоянии квадрат модуля коэффициента Поэтому для нормированных волновых функций
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значенияволновой функции этого состояния в координатном представлении.
Волновая функция
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2014; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.204 (0.008 с.) |

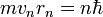 , где n — натуральные числа, а
, где n — натуральные числа, а 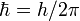 — постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.
— постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.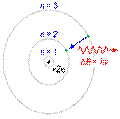 Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома
Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модельатома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]:
Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модельатома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]:  .
.
 , описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.
, описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.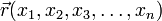 , в определенный момент времени t она будет иметь вид
, в определенный момент времени t она будет иметь вид 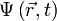 . В таком случае уравнение Шрёдингера запишется в виде:
. В таком случае уравнение Шрёдингера запишется в виде: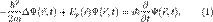
 ,
,  — постоянная Планка;
— постоянная Планка;  — масса частицы,
— масса частицы, 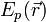 — внешняя по отношению к частице потенциальная энергия в точке
— внешняя по отношению к частице потенциальная энергия в точке  — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид: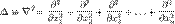
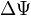 в декартовой системе координат заменяется выражением
в декартовой системе координат заменяется выражением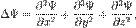

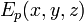 — потенциальная энергия в точке
— потенциальная энергия в точке 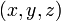
 не является функцией времени, можно записать в виде:
не является функцией времени, можно записать в виде:
 должна удовлетворять уравнению:
должна удовлетворять уравнению:
 от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции
от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции  в уравнении (2). Она производится следующим путём: временна́я зависимость функции
в уравнении (2). Она производится следующим путём: временна́я зависимость функции 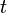 в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель
в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель  умножаетсяна потенциальную энергию
умножаетсяна потенциальную энергию 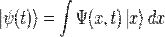
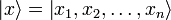 — координатный базисный вектор, а
— координатный базисный вектор, а 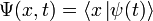 — волновая функция в координатном представлении.
— волновая функция в координатном представлении.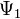 и
и  , то она может пребывать и в состоянии, описываемом волновой функцией
, то она может пребывать и в состоянии, описываемом волновой функцией при любых комплексных
при любых комплексных  и
и  .
.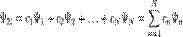 .
. определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией
определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией 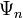 .
. .
.