
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовий гармонічний осциляторСодержание книги
Поиск на нашем сайте В квантовій теорії поняття енергії втрачає сенс, тому квантовий гармонічний осцилятор визначається як поведінка частини маси m з потенціальною енергією U(x) такою ж як у класичного осцилятора, а саме
Видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а і +а кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а) класичний осцилятор вийти не може. Квантовим осцилятором може бути лише елементарна частинка, яка поряд із корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Згідно класичної механіки осцилятор здійснює гармонічні коливання з циклічною частотою Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:
Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд 20. Квантова механіка системи тотожних частинок Симетричні і антисиметричні стани. Принцип Паулі..Хвильова функція електрона з урахуванням спіну Незвичайні, з класичної точки зору властивості, проявляються при вивченні руху системи квантових частинок. Квантова теорія систем частинок полягає в тому, що в цій теорії поняття хвильової функції відноситься лише до системи частинок. Кожна окрема частинка системи не знаходиться в певному квантовому стані і не може бути охарактеризована своєю хвильовою функцією, яка б залежала лише від параметрів даної частинки. Система квантових частинок набуває властивостей, яким не має аналога ні в класичній фізиці ні в квантовій механіці однієї частинки. Специфічна особливість квантової теорії систем частинок полягає в їх принциповій нерозрізненості. Всі частинки такої квантової системи є тотожними. Нерозрізненість тотожних частинок в квантових системах не властива для систем класичних частинок, де кожна частинка системи має свою індивідуальність. В квантовій фізиці однакові частинки втрачають свою індивідуальність, так як рухаються не по траєкторіях. Поняття траєкторії квантових частинок із за хвильових властивостей втрачає будь-який фізичний зміст. Із принципової нерозрізненості однакових частинок випливає, що перестановка місцями двох однакових частинок в системі не впливає ні на одну із фізичних величин, що характеризують цю систему.
Симетричні і антисиметричні стани. Нехай хвильова функція описує стан системи, яка містить N однакових частинок. Діючи на неї оператором перестановки Тут індекси та позначають, відповідно, симетричну і антисиметричною хвильові функції, а перестановки проводяться по всім парам частинок системи. Такий розподіл має абсолютний характер, тобто вид симетрії хвильових функцій не змінюється з часом. Якщо хвильова функція, що описує стан системи, в будь-який момент часу є симетричною (антисиметричною), то цей тип симетрії зберігається і в будь-який інший момент часу. Принцип Паулі. При́нцип ви́ключення Па́улі (або принцип заборони Паулі)— квантово-механічний принцип, згідно з яким у багаточастинковій системі невзаємодіючих ферміонів, жодні дві частки не можуть описуватися одночастинковими хвильовими функціями із однаковим набором усіх квантових чисел.Принцип був сформульований Вольфгангом Паулі в 1925 році. Він є наслідком принципу нерозрізнюваності часток (або принципу тотожності частинок).Ферміони характеризуються тим, що їхні хвильові функції антисиметричні щодо перестановки ідентичних частинок. Щоб забезпечити антисиметричність, хвильову функцію системи багатьох ферміонів зазвичай будують за допомогою детермінанта Слейтера, використовуючи певний набір одночастинкових хвильових функцій. Із цих одночастинкових функцій не може бути двох однакових, бо згідно з властивостями визначника при двох однакових рядках чи стовпчиках визначник дорівнює нулю. Наслідок для атомів, молекул та твердих тіл При побудові стану багаточастинкової квантовомеханічної системи із одноелектронних станів два електрони не можуть знаходитися в однаковому стані. Здебільшого спінова підсистема незалежна від координатної, тож, враховуючи дві можливі проекції спіна, один орбітальний стан можуть займати два електрони із протилежними спінами. Електронні конфігурації атомів і молекул будуються з врахуванням цього фактора. Принцип Паулі формально означає неявну взаємодію у багаточастинковій системі, навіть коли явної взаємодії нема, оскільки знаючи стан однієї частинки, точно відомо, що жодна інша частинка не перебуває у цьому стані.Розглянемо два електрони, просторові координати яких збігаються, тоді якщо спінові координати теж збігаються (спіни співнапрямлені), то електрони не можуть перебувати в одній точці, але якщо спіни напрямлені у протилежні сторони, то електрони можуть знаходитися в одній точці простору.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , χ – постійна. Графіком цієї функції є парабола.
, χ – постійна. Графіком цієї функції є парабола.
 . Виразимо χ через ω та m, отримаємо
. Виразимо χ через ω та m, отримаємо  .
. де m ― маса квантової частинки;
де m ― маса квантової частинки;  ― власна циклічна частота; Е ― повна енергія частинки.
― власна циклічна частота; Е ― повна енергія частинки. де n= 0,1,2,3,... ― будь-яке ціле число, починаючи з нуля;
де n= 0,1,2,3,... ― будь-яке ціле число, починаючи з нуля;  ― власна циклічна частота осцилятора;
― власна циклічна частота осцилятора;  ― стала Дірака. Аналізуючи дане рівняння бачимо, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:
― стала Дірака. Аналізуючи дане рівняння бачимо, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:  ,
,  ,
,  Отже, енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії рівних нулю.
Отже, енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії рівних нулю. , отримуємо
, отримуємо (1) Власними функціями оператора є функції, які при перестановці координат і-ої або j-ої частинок або залишаються незмінними (
(1) Власними функціями оператора є функції, які при перестановці координат і-ої або j-ої частинок або залишаються незмінними ( ), або змінюють знак (
), або змінюють знак (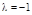 ). Ці функції називаються відповідно симетричними і антісімметрічние щодо перестановки частинок.Отриманий результат означає, що стану системи з N однакових частинок описуються хвильовими функціями, які або не змінюються (симетричні), або змінюють знак (антисиметрична) при перестановці місцями будь-якої пари частинок. Хвильові функції, що описують стан системи, не можуть бути симетричними при перестановці однієї частини частинок системи і антісімметрічние при перестановці іншій частині частинок. Симетрія або антисимметрія хвильових функцій зберігається по відношенню до перестановок всіх частинок системи.
). Ці функції називаються відповідно симетричними і антісімметрічние щодо перестановки частинок.Отриманий результат означає, що стану системи з N однакових частинок описуються хвильовими функціями, які або не змінюються (симетричні), або змінюють знак (антисиметрична) при перестановці місцями будь-якої пари частинок. Хвильові функції, що описують стан системи, не можуть бути симетричними при перестановці однієї частини частинок системи і антісімметрічние при перестановці іншій частині частинок. Симетрія або антисимметрія хвильових функцій зберігається по відношенню до перестановок всіх частинок системи.




