
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Експериментальні основи квантової механікиСодержание книги
Поиск на нашем сайте
Існують такі експерименти, які неможливо пояснити без залучення квантової механіки. Перший різновид квантових ефектів — квантування певних фізичних величин. Якщо локалізувати вільну частинку з розглянутого вище прикладу у прямокутній потенціальній ямі — області протору розміром L, обмеженій з обох боків нескінченно високим потенціальним бар'єром, то виявиться, що імпульс частинки може мати лише певні дискретні значення
де h — стала Планка, а n — довільне натуральне число. Про параметри, які можуть набувати лише дискретних значень кажуть, що вони квантуються. Прикладами квантованих параметрів є також момент імпульсу, повна енергія обмеженої у просторі системи, а також енергія електромагнітного випромінювання певної частоти.
Ще один квантовий ефект — це корпускулярно-хвильовий дуалізм. Можна показати, що за певних умов проведення експерименту, мікроскопічні об'єкти, такі як атоми або електрони, набувають властивостей частинок (тобто можуть бути локалізовані в певній області простору). За інших умов, ті самі об'єкти набувають властивостей хвиль та демонструють такі ефекти, як інтерференція.
Наступний квантовий ефект — це ефект сплутаних квантових станів. В деяких випадках вектор стану системи з багатьох частинок не може бути поданий як сума окремих хвильових функцій, які б відповідали кожній з частинок. В такому випадку кажуть, що стани частинок сплутані. І тоді, вимірювання, яке було проведено лише для однієї частинки, матиме результатом колапс загальної хвильової функції системи, тобто таке вимірювання буде мати миттєвий вплив на хвильові функції інших частинок системи, хай навіть деякі з них знаходяться на значній відстані. (Це не суперечить спеціальній теорії відносності, оскільки передача інформації на відстань в такий спосіб неможлива.)
Математичні основи квантової механіки Квантова механіка - фундаментальна фізична теорія, що в описі мікроскопічних об'єктів розширює, уточнює і поєднує результати класичної механіки і класичної електродинаміки. Оператором
Для обчислення середніх значень координати x та імпульсу p частинки в стані, що описується хвильовою функцією ψ(х), необхідно виконати такі операції: де символом Кожний вимірюваний параметр с-ми представляється ермітовим оператором у просторі станів. Кожний власний стан вимірюваного параметру відповідає власному вектору оператора, а відповідне власне значення дорівнює значенню вимірюваного параметру в даному власному стані. В процесі вимірювання, ймовірність переходу системи в один із власних станів визначається як квадрат скалярного добутку вектора власного стану та вектора стану перед вимірюванням. Принципу невизначеності Гейзенберга відповідає те, що оператори відповідних фізичної величин не комутують між собою. Аналітичний розв'язок рівняння Шредінгера існує для невеликої кількості гамільтоніанів. Проте існують певні методи наближеного розв'язку цих рівнянь. Наприклад, методи теорії збурень, «квазікласичного рівняння руху».
Рівн Шредінгера. Стаціо і загальне ріівн Шредінгера. Власт стаціонарних станів Рівняння Шредінгера - основне рівняння нерелятивістської квантової механіки, яке визначає закон еволюції квантової системи з часом.
,де Внаслідок квантового принципу суперпозиції станів рівняння, що описує еволюцію системи, має бути лінійним. Рівняння Шредінгера є саме таким. Рівняння Шредінгера не лоренц-інваріантне, тобто справедливе лише для частинок, швидкість яких набагато менша за швидкість світла. Загальніше рівняння Дірака переходить у рівняння Шредінгера при малих швидкостях. Тому при взаємодії з магнітним полем (яке є чисто релятивістським явищем) не можна використовувати звичайне рівняння Шредінгера. Комплексно спряжене рівняння Рівняння Шредінгера не виводиться, а постулюється. Правильність цього рівняння підтверджується узгодженням з експериментами, що, у свою чергу, надає йому характер закону природи. З погляду математики рівняння Шредінгера є лінійним диф. рівнянням з частинними похідними. Відомо, що такі р-ня мають багато розв’язків, причому таких, що лінійна комбінація будь-якої сукупності розв’язків рівняння також буде розв’язком рівняння. Існує формальний розв'язок рівняння Шредінгера
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.118 (0.007 с.) |

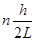
 називають рецепт, за яким за заданою функцією ψ(х) знаходять іншу функцію φ(х):
називають рецепт, за яким за заданою функцією ψ(х) знаходять іншу функцію φ(х):


 позначено операцію диференціювання.
позначено операцію диференціювання.
 - хвильова функція, H - гамільтоніан.
- хвильова функція, H - гамільтоніан. збігається з рівнянням Шредінгера, якщо замінити t на −t, а хвильову функцію
збігається з рівнянням Шредінгера, якщо замінити t на −t, а хвильову функцію  на
на  . Цей факт відображає зворотність процесів у квантовій механіці.
. Цей факт відображає зворотність процесів у квантовій механіці.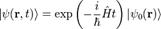 Тут
Тут  є не числом, а оператором, який називають оператором еволюції.
є не числом, а оператором, який називають оператором еволюції.


