
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантова теорія випромінюванняСодержание книги
Поиск на нашем сайте Густина енергії рівноважного випромінювання. Розглянемо основні положення теорії рівноважного теплового випромінювання. Для цього, не обмежуючи спільності висновків, припустимо, що порожнина з ідеально відбивають стінками має форму куба з ребром. Помістимо в цю порожнину мале за розмірами абсолютно чорне тіло, що має температуру. За рахунок випускання і поглинання електромагнітних хвиль цим тілом порожнину рівномірно заповниться рівноважним тепловим випромінюванням з певною об'ємної щільністю енергії, що залежить від температури. Цю інтегральну об'ємну щільність енергії теплового випромінювання можна розкласти по спектру частот, тобто представити у вигляді
Тут функція
30, Термодинам́ічні парáметри, ентропія, хімічний потенціал. Термодинам́ічні парáметри — це величини, що можуть змінюватися із зміною самої системи внаслідок її взаємовпливу з навколишнім середовищем. Термодинамічні парамтери можна поділити на основні та допоміжні. До основних термодинамічних параметрів належать такі, які легко визначити простими технічними засобами, як-от тиск, температура та питомий обє'м. Сукупність зазначених основних термодинамічних параметрів визначає стан системи у даний момент. Термодинамічні параметри: -температура\ -густина -теплоємність -питомий електричний опір і багато інших фізичних величин Ентропія - це скорочення доступної енергії речовини в результаті передачі енергії. Абсолютна ентропія (S) речовини або процесу - це зміна доступної енергії при теплопередачі при даній температурі (Btu / R, Дж / К). Математично ентропія дорівнює теплопередачі, поділеній на абсолютну температуру, при якій відбувається процес. Отже, процеси передачі великої кількості теплоти більше збільшують ентропію. Також зміни ентропії збільшаться при передачі теплоти при низькій температурі. Так як абсолютна ентропія стосується придатності всієї енергії всесвіту, температуру зазвичай вимірюють в абсолютних одиницях (R, К).Питому ентропію (S) вимірюють щодо одиниці маси речовини. Температурні одиниці, які використовуються при обчисленні різниць ентропії станів, часто наводяться з температурними одиницями в градусах за Фаренгейтом чи Цельсієм. Прагнення термодинамічних систем до встановлення рівноваги за складом кількісно характеризується величиною, яка називається хімічним потенціалом. Для визначення хімічного потенціалу потрібно знайти різницю між енергією системи із N+1 часткою і системи із N частками. Хімічний потенціал - це енергія, на яку потрібно надати частці, щоб помістити її в термодинамічну систему. Важливо при цьому пам'ятати, що частка поміщаєтсья в систему таким чином, щоб перебувати в тепловій рівновазі з іншими частками. Визначення хімічного потенціалу через інші термодинамічні потенціали можна записати у вигляді:
де Е — повна енергія системи, S — її ентропія, N — кількість частинок в системі. Ця формула визначає, окрім хімічного потенціалу, також тиск P і температуру T. Можна довести, що хімічний потенціал задається формулою Якщо енергія системи залежить не від об'єму, а від інших термодинамічних параметрів, А1, А1 …початкова формула приймає вигляд
31, Перший закон термодинаміки. Пе́рший зако́н термодина́міки — одне з основних положень термодинаміки, є, по суті, законом збереження енергії у застосуванні до термодинамічних процесів. Перший закон термодинаміки сформульований в середині 19 століття в результаті робіт Саді Карно, Юліуса фон Маєра, Джеймса Прескотта Джоуля і Германа фон Гельмгольца. Перший початок термодинаміки часто формулюють як неможливість існування вічного двигуна 1-го роду, який здійснював би роботу, не черпаючи енергію з якого-небудь джерела. Перший закон термодинаміки Зміна внутрішньої енергії закритої системи, яка відбувається в рівноважному процесі переходу системи із стану 1 в стан 2, дорівнює сумі роботи, зробленої над системою зовнішніми силами, і кількості теплоти, наданої системі: ΔU = A' + Q. Робота здійснена системою над зовнішніми тілами в процесі 1->2 (Назвемо її просто А) A=-A', тоді закон приймає вигляд: Кількість теплоти, що надається системі, витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил. Для елементарної кількості теплоти δQ; елементарної роботи δA і малої зміни dU внутрішньої енергії перший закон термодинаміки має вигляд:
32, Друге начало термодинаміки. Формулювання: Для системи із сталою температурою існує певна функція стану S — ентропія, яка визначається таким чином, що 1. Адіабатичний перехід із рівноважного стану A в рівноважний стан B можливий лише тоді, коли
2. Приріст ентропії в повільному квазістатичному процесі дорівнює де T — температура. Історична довідка Другий закон термодинаміки був сформульваний у середині 19-го століття. Досліди Майєра й Джоуля встановили еквівалентність між тепловою й механічною енергіями (перший закон термодинаміки). Виникло питання про ефективність теплових машин. Експериментальні дослідження свідчили про те, що частина тепла обов'язково втрачається при роботі будь-якої машини. У 1850-х, 1860-х роках Клаузіус у низці публікацій розробив поняття ентропії. В 1865 році він нарешті обрав для нового поняття ім'я. Ці публікації довели також, що тепло неможливо повністю перетворити в корисну роботу, сформулювавши таким чином другий закон термодинаміки. 33, Третє начало термодинаміки. Теорема Нернста, відома також під назвою третій закон термодинаміки, стверджує, що ентропія прямує до нуля при абсолютному нулі температури. Вперше закон спадання ентропії до нуля при нульовій температурі сформулював Вальтер Нернст (Нобелівська премія з хімії 1920 року). Обґрунтування Теорема Нернста базується на квантвомеханічних уявленнях. У класичній фізиці ентропія визначена з точністю до сталої, тому можна стверджувати лише те, що при нульовій температурі ентропія приймає мінімальне значення. Згідно з квантовою механікою при абсолютному нулі температури фізичне тіло перебуває в основному стані. Такий стан єдиний. Оскільки
де S — ентропія, k — стала Больцмана, Γ — кількість можливих станів, ентропія системи дорівнює нулю. Наслідки Внаслідок теореми Нернста при абсолютному нулі нульове значення мають також і ряд інших термодинамічних величин, наприклад: темлоємність і коефіцієнт теплового розширення. До нуля прямують як теплоємність при сталому обє'мі cV, так і теплоємність при сталому тиску cP, при чому
34, Метод термодинамічних потенціалів і метод циклів. Метод термодинамічних потенціалів (Дж. Гіббс, 1874—1878), заснований на спільному вживанні 1-го і 2-го початків Т., дозволяє отримати ряд важливих термодинамічних співвідношень між різними фізичними властивостями системи. Так, використання незалежності других змішаних похідних від порядку диференціювання приводить до зв'язку між теплоємкостямі с р і c v, коефіцієнтом теплового розширення і ізотермічним коефіцієнтом стискування до співвідношення між ізотермічним і адіабатичним коефіцієнтами стискування і т. п. З умови, що ізольована система в рівноважному стані володіє максимальним значенням ентропії, витікає умова мінімальності термодинамічних потенціалів в рівноважному стані по відношенню до довільних малих відхилень від рівноваги при фіксованих значеннях відповідних незалежних змінних. Це приводить до важливих нерівностей (умовам стійкості), зокрема, c p > c v > 0.
36, Статисти́чна фі́зика — розділ теоретичної фізики, що вивчає поводження систем з дуже великим числом часток у стані локальної рівноваги. Звичайно, при дослідженні таких систем нас не цікавить майже випадкове поводження кожної конкретної мікроскопічної частки. Статистична фізика саме відслідковує, як з таких мікроскопічних рухів складається усереднена еволюція системи в цілому. Статистична фізика дає мікроскопічний висновок термодинаміки багатьох реальних систем: ідеальних газів, реальних газів, квантових газів, простих конденсованих середовищ (наприклад, ідеальних кристалів, спінових ланцюжків). Зокрема, вона дає тлумачення фізичної природи запроважденого в термодинаміці терміну ентропії, і пояснює закон неспадання ентропії. Статистична фізика не описує те, як саме система приходить у стан локальної рівноваги; цю первісну еволюцію системи після її приготування описуєфізична кінетика. Частина статистичної фізики, яка вивчається в шкільному курсі, зветься молекулярною фізикою і є, по суті, більш-менш докладний виклад властивостейідеального газу.
37, Рівняння Ван дер Ваальса — модельне рівняння стану неідеального газу.
де P — тиск, V — об'єм, N — число молекул, T — температура, kB — стала Больцмана, a та b — характерні для кожного реального газу сталі, які будуть визначені нижче. Рівняння ван дер Ваальса описує збільшення тиску при зменшенні об'єму розріджених газів, перенасичену пару, перегріту рідину, різке зменшення стисливості в рідкій фазі. Рівняння ван дер Ваальса визначає також критичну температуру, вище якої газ не зріджується при жодному тиску. Фактично рівняння Ван дер Ваальса описує різницю між станом реального таідеального газів. Поправки a і b мають більше значення при високих тисках газів. Наприклад, для азоту при тиску порядку 80 атм розрахунки проведені за рівняннями ідеального та реального газів різняться приблизно на 5%, а при тиску порядку 400 атм різниця складає вже 100%. Рівняння ван дер Ваальса описує газ, молекули якого взаємодіють між собою. Потенціальна енергія взаємодії між двома молекулами задається функцією U(r), де r — відстань між молекулами. Молекули притягаються на великих відстанях і відштовхуються, підходячи близько одна до одної. Притягування зумовлене ван дер Ваальсовими силами, а відштовхування —принципом Паулі.
38, Теорія флуктуацій Флуктуація (від лат fluctuatio -. Коливання) - термін, що характеризує будь-яке коливання чи будь-яке періодичне зміна. У квантовій механіці - випадковівідхилення від середнього значення фізичних величин, які характеризують системуз великого числа частинок, викликаються тепловим рухом частинок абоквантовомеханічними ефектами.
39, Броунівський рух. Теорія Ейнштейна-Смолуховського Бро́унівський рух — невпорядкований, хаотичний рух дрібних частинок речовини в розчинах. Названий на честь ботаніка Роберта Брауна, який спостерігав[1] це явище під мікроскопом у 1827 р.. Теорію броунівського руху побудував у 1905 р. Альберт Ейнштейн. Відкриття й пояснення броунівського руху мало велике значення для фізики, оскільки було свідченням теплового руху молекул. Браун 1827 року відкрив хаотичний рух спор плауна у воді. Рух завислих частинок відбувався внаслідок руху молекул. Таким же чином рухаються частинки фарби у воді, пилинки в променях світла тощо. Молекули рідини зіштовхуються з завислими у ній частинками, а отже передають їм імпульс
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 .
. визначає об'ємну щільність енергії випромінювання, що припадає на одиничний інтервал частот поблизу частоти
визначає об'ємну щільність енергії випромінювання, що припадає на одиничний інтервал частот поблизу частоти  . Назвемо її спектральною щільністю енергії теплового. випромінювання при даній температур
. Назвемо її спектральною щільністю енергії теплового. випромінювання при даній температур  і.
і.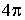 . Тому щільність енергії випромінювання, що припадає на тілесний кут
. Тому щільність енергії випромінювання, що припадає на тілесний кут  , тобто падаючого на майданчик під кутом до її нормалі, можна за. писати у вигляді
, тобто падаючого на майданчик під кутом до її нормалі, можна за. писати у вигляді 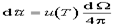









 .
.


