
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Математический аппарат квантовой механикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Глава 2. Математический аппарат квантовой механики Уравнение Шредингера Для того, чтобы определить волновую функцию Для свободной нерелятивистской частицы
С другой стороны, её волна де Бройля (
Рассмотрим производные:
Последнему выражению можно сопоставить следующее равенство
Это уравнение и является уравнением Шредингера для свободного одномерного движения. Проделанная процедура не есть получение уравнения, а просто наводящие соображения для его написания. Обобщение на трехмерный случай (свободная частица
Исходя из того, что полная энергия частицы во внешнем поле равна
получаем
Если ввести оператор Гамильтона - гамильтониан
то уравнение Шредингера примет вид
В таком виде мы имеем нестационарное уравнение Шредингера - основное динамическое уравнение нерелятивистской волновой механики. Оно играет такую же важную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в теории электромагнитного поля. Уравнение Шредингера описывает изменение во времени поведения микрообъектов, характеризуемых волновой функцией В стационарном случае, когда гамильтониан не зависит от времени, можно разделить уравнение (2.9) на два уравнения - для координатной и временной частей волновой функции. Для этого подставим волновую функцию в виде
в уравнение Шредингера.
Поделив обе части уравнения на полную функцию
Левая часть уравнения зависит только от времени t, а правая часть зависит только от пространственных координат. Поскольку это равенство справедливо при произвольных значениях независимых переменных, то обе части уравнения равны константе - константе разделения, которую обозначим через Е. Итак, мы имеем 2 уравнения. Первое уравнение
имеет решение
Уравнение для координатной части волновой функции
или
называется стационарным уравнением Шредингера. Полная волновая функция стационарного состояния имеет вид
где y(r) – решение стационарного уравнения Шредингера. Плотность вероятности распределения Операторы Операторный метод - традиционная и основная формулировка квантовой механики. В квантовой механике любой динамической переменной, любой физической величине приводится в соответствие квантово-механический оператор. Оператор
Ранее мы уже встречались с операторами: В квантовой механике применяются только линейные операторы, чтобы не нарушался принцип суперпозиции состояний. Свойство линейных операторов:
где С 1, С 2 - произвольные постоянные. Основные операторы квантовой механики в координатном представлении: 1) Оператор координаты:
2) Оператор полной энергии (гамильтониан)
является суммой операторов кинетической
и потенциальной энергии
3) Оператор импульса. Исходя из выражения для кинетической энергии
Оператор проекции импульса на ось x
4) Оператор момента импульса
Действия с операторами: 1) Суперпозиция
2) Сумма операторов
3) Произведение операторов
Вообще говоря, операторы
и антикоммутатор
Если для двух операторов выполняется условие
т.е. их коммутатор равен нулю, то говорят, что эти операторы коммутируют. Для того, чтобы найти коммутатор, надо подействовать им на произвольную функцию
Очевидно, что операторы Собственные функции и собственные значения В квантовой механике каждой физической величине сопоставляется оператор. Рассмотрим задачу определения собственных чисел f и g, и собственных функций j и y операторов
где n - значок, соответствующий номеру решения. Собственные функции - это такие функции, которые под действием оператора Спектр собственных значений может быть дискретным и непрерывным. Дискретный спектр gn имеет место, если уравнение Решения стационарного уравнения Шредингера Свойства d- функции. Функция
Геометрически d-функцию можно рассматривать как предел максимума, стремящегося к бесконечности в точке a и сохраняющего площадь под кривой равной единице. Важное свойство d- функции состоит в том, что она “вырезает” из функции в подынтегральном выражении значение этой функции в точке a
Последнее условие и нормировка позволяет получать коэффициенты
Потенциальные барьеры
 . Если на каком-то участке координаты x потенциальная энергия возрастает (или падает), то говорят об одномерной потенциальной ступеньке. . Если на каком-то участке координаты x потенциальная энергия возрастает (или падает), то говорят об одномерной потенциальной ступеньке.
Рассмотрим задачу, когда на одномерную потенциальную ступеньку налетает частица. Если выполняется условие, что размер области изменения потенциальной энергии D x мал по сравнению с волной де Бройля частицы В классическом случае, если энергия налетающей частицы E < U 0, то частица с достоверностью отражается и в правую область не проникает. Если ее энергия E > U 0, тогда частица с достоверностью проходит над барьером и в правой области она движется с меньшей скоростью Прямоугольный потенциальный барьер. Пусть на прямоугольный потенциальный барьер (Рис.3.6) слева падает поток частиц с полной энергией
Рис.3.6. Прохождение частицы сквозь прямоугольный потенциальный барьер.
Потенциальная энергия
Разобьем пространство на три части I, II и III. В I и III областях имеем уравнение Шредингера для свободной частицы:
Его решения: I область III область Во II области имеем:
Соответствующее решение под барьером
Волна exp (ikx) движется в положительном направлении оси x, а волна exp (- ikx) - в обратном. В III области не будет волны в обратном направлении оси x, т.к. из бесконечности нет потока частиц. Окончательно
На границах полная волновая функция и ее первая производная непрерывны. Эти граничные условия дают систему уравнений для определения коэффициентов A, B, C, D и G. При x = 0
При x = a Введем коэффициенты отражения и прохождениякак отношение плотностей потока
В I области поток вправо определяется волной, распространяющейся вдоль оси x,
Поток влево в I области определяется волной
Коэффициент отражения определяется
Коэффициент прохождения (поток пройденной волны определяется волной
В первой паре уравнений (3.32) сложим два уравнения, избавляясь от коэффициента В.
Во второй паре уравнений (3.33) делим на a второе уравнение, затем складывая и вычитая, получаем следующие два соотношения:
Выражая отсюда 2 С и 2 D и подставляя их в предыдущее уравнение, имеем
Раскрывая скобки, получаем
Введем гиперболический косинус и гиперболический синус:
Для них выполняется теорема Пифагора Тогда:
Теперь, раскрывая скобки и учитывая теорему Пифагора, получаем для отношения квадратов:
Здесь Результирующее выражение для коэффициента прохождения имеет вид
Исследование коэффициентов прохождения и отражения. То, что коэффициент прохождения не равен нулю при полной энергии частицы меньшей потенциального барьера E < U 0 – называется туннельным эффектом. В классической физике ничего подобного нет, туннельный эффект – чисто квантовый эффект. При условии a a >> 1 можно получить для коэффициента прохождения Т:
или Коэффициент отражения определяется соотношением
Как и должно быть из закона сохранения вероятности
Случай E > U 0. Решение получается тем же путем, как и ранее, только в области II имеем решение, описывающее движение свободной частицы с
В общем случае мы имеем коэффициент отражения не равный нулю Однако, есть характерные энергии, когда коэффициент отражения равен 0, а коэффициент прохождения равен 1:
При таких энергиях частица пролетает над барьером с достоверностью и при квантовом рассмотрении. Заметим, что при этом целое число полуволн де Бройля укладывается на барьере, чему соответствует условие Аналогичное решение для коэффициентов прохождения и отражения получаем для барьера в виде прямоугольной ямы, при этом меняется только " U 0" на "- U 0". Отметим, что в общем случае коэффициент отражения не равен нулю. Коэффициент прохождения обращается в единицу только для таких энергий когда на размере ямы укладывается целое число полуволн де Бройля. Барьер произвольной формы.
Рис.3.7. Прохождение частицы сквозь потенциальный барьер произвольной формы.
Приближенно задачу можно решить, если барьеры достаточно широкие, и при этом импульс p (x) и соответствующая волна де Бройля
Тогда связь волновой функции на выходе из барьера с волновой функцией на входе записывается, как
Коэффициент прохождения через барьер произвольной формы
Здесь мы поменяли местами потенциальную и полную энергии частицы. В итоге
Выражение (3.47) позволяет найти коэффициент прохождения через барьер произвольной формы в квазиклассическом приближении.
Глава 4. Момент импульса Глава 5. Физика атомов Уравнение для угловой части Угловая часть волновой функции находится из уравнения
Записывая явный вид оператора Лежандра, имеем
Перепишем (5.19) в виде
Уравнение для угловой части не зависит от конкретного вида потенциала U (r) и для всех центральных полей имеет одно и то же решение. Это уравнение также можно разделить, если подставить в (5.20)
Действуя, как и ранее, получаем
Это уравнение называется присоединенным уравнением Лежандра. Из математики известно, что его решения имеют вид
Функции
Полиномы Лежандра определяются формулой Родригеса
Приведем значения некоторых из присоединенных полиномов Лежандра:
Соответствующие сферические гармоники
Теперь мы можем записать полное решение уравнения Шредингера для атома водорода (в атомной системе единиц)
Уровень
т.е. каждому
Магнитный момент атома Из курса общей физики известно, что магнитный и орбитальный моменты электрона связаны соотношением
Знак минус показывает, что магнитный и орбитальный моменты электрона направлены в противоположные стороны. Отношение магнитного момента к орбитальному Из релятивистской теории Дирака и эксперимента следует, что для что магнитного и спинового моментов электрона имеет место соотношение
в котором коэффициент пропорциональности в два раза, чем в выражении (5.31). Иначе говоря, спин обладает удвоенным магнетизмом. В стационарном состоянии определенны значения могут иметь только модуль магнитного момента и его проекция на выделенную ось:
Мы ввели в (5.33) магнетон Бора Для атомного спина:
При S=1/2 ms =1/2, -1/2, Полный магнитный момент атома. Рассмотрим
Отсюда следует, что вектор полного магнитного момента
В силу (5.35)
Подставляя сюда явные выражения для
Сравнивая это выражение с (5.36), получаем фактор Ланде
Теперь
Отметим ряд наиболее интересных случаев: · в состоянии 5 · в состоянии 4 · в состоянии 6
Глава 6. Теория возмущений Таблица 1.
Состояние До сих пор мы рассматривали только систему независимых фермионов. В присутствии взаимодействия многочастичные волновые функции должны выражаться в виде линейных комбинаций типа
Приложение 2. Операторы в формализме чисел заполнения (вторичного квантования). Представим себе исходную систему, которая находится в состоянии Для фермионных операторов вводятся правила:
Отсюда следует, например, что:
Все состояния можно получить, действуя операторами
Из (П2.1) следует, что операторы
где знак “
Для фермионных операторов рождения и уничтожения выполняются коммутационные соотношения:
В коммутационных соотношениях уже заложены свойства антисимметрии волновой функции по отношению к перестановкам частиц. Все операторы квантовой механики можно записать в виде различных комбинаций этих двух операторов. Для этого потребуем равенства матричных элементов оператора, вычисленных в формализме чисел заполнения (вторичного квантования), и в обычном формализме квантовой механики. Тогда одночастичный оператор
в представлении чисел заполнения будет иметь вид
Чтобы убедиться в этом, достаточно рассмотреть
Аналогичным образом показывается, что двухчастичный оператор (потенциал межэлектронного взаимодействия
принимает вид
где Результаты (П2.5) и (П2.6) остаются справедливыми и для бозонов. При этом надо только изменить соотношения антикоммутации (П2.4.) на соотношения коммутации. Таким образом, многочастичный гамильтониан системы N взаимодействующих электронов (в поле N ионов) во внешнем потенциале
на языке вторичного квантования записывается в виде
где К сожалению, из-за наличия слагаемых типа гамильтониан Хаббарда - гамильтониан Гейзенберга - В последнем выражении
Литература. 1. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механика (серия Теоретическая физика, том 3), Москва, Физматлит, 2001г. 2. И. Е. Иродов, Квантовая физика, Москва, Физматлит, 2002г. 3. Д.И. Блохинцев, Основы квантовой механики. Москва, Высшая школа, 1983. ОГЛАВЛЕНИЕ
Глава 1. Введение 4 §1.1. Корпускулярно-волновой дуализм 4 §1.2. Волныде Бройля и их экспериментальное подтверждение 6 §1.3. Статистическое толкование волн де Бройля и соотношение неопределенностей 10 Глава 2. Математический аппарат квантовой механики 15 §2.1. Уравнение Шредингера 15 §2.2. Операторы. Собственные функции и собственные значения 19 §2.3. Самосопряженные (эрмитовы) операторы и их свойства 24 §2.4. Вычисление средних значений. Обозначения Дирака 30 §2.5. Дифференцирование операторов по времени 32 Глава 3. Уравнение Шредингера в одном измерении 33 §3.1. Одномерная потенциальная яма с бесконечно высокими | |||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 в общем случае используется основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (1926г.). Оно не выводится, а вводится как новый принцип, который затем проверяется на эксперименте. Это уравнение удовлетворяет требования, которые вытекают из самых общих физических соображений. Во-первых, оно должно быть линейным уравнением, т.к. должен выполняться принцип суперпозиции. Во-вторых, уравнение должно содержать только фундаментальные константы, например e, m, h.
в общем случае используется основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (1926г.). Оно не выводится, а вводится как новый принцип, который затем проверяется на эксперименте. Это уравнение удовлетворяет требования, которые вытекают из самых общих физических соображений. Во-первых, оно должно быть линейным уравнением, т.к. должен выполняться принцип суперпозиции. Во-вторых, уравнение должно содержать только фундаментальные константы, например e, m, h. (2.1)
(2.1) )
) (2.2)
(2.2)


 ) тривиально:
) тривиально:
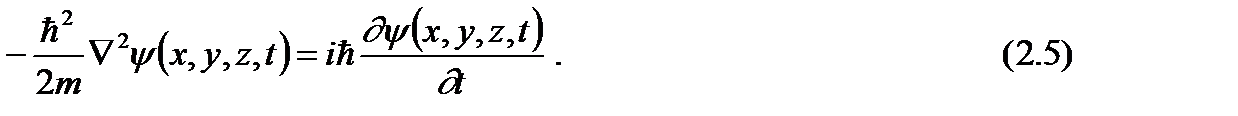




 .
.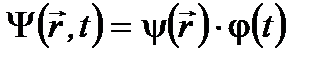 (2.10)
(2.10)
 , имеем
, имеем





 не зависит от времени, т.е. стационарна.
не зависит от времени, т.е. стационарна. - это правило, по которому любой выбранной функции j приводится в соответствие другая функция f:
- это правило, по которому любой выбранной функции j приводится в соответствие другая функция f:
 . При использовании операторов имеется договорное условие: оператор пишется всегда слева от функции, которая стоит справа от него и оператор действует на все, что стоит справа от него (если нет ограничивающих скобок).
. При использовании операторов имеется договорное условие: оператор пишется всегда слева от функции, которая стоит справа от него и оператор действует на все, что стоит справа от него (если нет ограничивающих скобок). , (2.19)
, (2.19)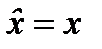 является оператором умножения;
является оператором умножения;


 , получим, что оператор импульса равен
, получим, что оператор импульса равен




 (
( ; (2.28)
; (2.28) и
и 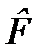 некоммутативны, т.е. их последовательное действие не совпадает с последовательным обратным действием:
некоммутативны, т.е. их последовательное действие не совпадает с последовательным обратным действием:  . Можно определить коммутатор двух операторов
. Можно определить коммутатор двух операторов

 , (2.31)
, (2.31)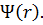 Например, не коммутируют операторы
Например, не коммутируют операторы  , коммутатор которых равен:
, коммутатор которых равен: 

 и
и 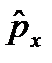 коммутируют, т.е.
коммутируют, т.е.  .
. (2.33)
(2.33) . Собственныеволновые функции описывают в квантовой механике такие состояния, в которых данная физическая величина gимеет определенное значениеgn. Иначе говоря, если частица (или система) находится в состоянии
. Собственныеволновые функции описывают в квантовой механике такие состояния, в которых данная физическая величина gимеет определенное значениеgn. Иначе говоря, если частица (или система) находится в состоянии  , то ее физическая величина g в этом состоянии равна gn и постоянна. Совокупность собственных значений gn называется спектром оператора
, то ее физическая величина g в этом состоянии равна gn и постоянна. Совокупность собственных значений gn называется спектром оператора  имеет решение не при всех, а только при определенных gn. Непрерывный или сплошной спектр gn имеет место, когда это уравнение имеет решение при всех значениях gn или хотя бы при всех gn в некоторой области. Спектр собственных значений может быть смешанным, т.е. состоящим из дискретных и непрерывных значений gn. Уравнение на собственные значения оператора координаты
имеет решение не при всех, а только при определенных gn. Непрерывный или сплошной спектр gn имеет место, когда это уравнение имеет решение при всех значениях gn или хотя бы при всех gn в некоторой области. Спектр собственных значений может быть смешанным, т.е. состоящим из дискретных и непрерывных значений gn. Уравнение на собственные значения оператора координаты  в координатном представлении квантовой механики имеет решение при всех значениях координаты, т.е. x имеет сплошной спектр. Собственные функции оператора проекции импульса
в координатном представлении квантовой механики имеет решение при всех значениях координаты, т.е. x имеет сплошной спектр. Собственные функции оператора проекции импульса  находятся из
находятся из  . Решения существуют при любых значениях px, т.е. оператор проекции импульса
. Решения существуют при любых значениях px, т.е. оператор проекции импульса  имеет непрерывный спектр.
имеет непрерывный спектр. зависят от вида оператора потенциальной энергии
зависят от вида оператора потенциальной энергии  . При этом можно получить как дискретный спектр (электрон в атоме водорода), так и непрерывный спектр (свободная частица).
. При этом можно получить как дискретный спектр (электрон в атоме водорода), так и непрерывный спектр (свободная частица). везде равна нулю за исключением точки x = a, где она обращается в бесконечность:
везде равна нулю за исключением точки x = a, где она обращается в бесконечность: или
или 
 или
или 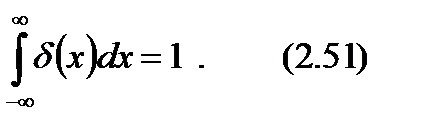

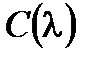 .
. , то тогда можно считать барьер прямоугольным, для которого
, то тогда можно считать барьер прямоугольным, для которого  .
. . В рамках квантово-механического рассмотрения решается уравнение Шредингера в области до порога x < 0 и после порога x > 0, а затем решения “сшиваются” на границе (x = 0).
. В рамках квантово-механического рассмотрения решается уравнение Шредингера в области до порога x < 0 и после порога x > 0, а затем решения “сшиваются” на границе (x = 0). , меньшей величины барьера.
, меньшей величины барьера. (3.25)
(3.25) . (3.26)
. (3.26)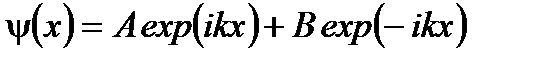 , (3.27)
, (3.27) . (3.28)
. (3.28) . (3.29)
. (3.29) (3.30)
(3.30) . (3.31)
. (3.31) . (3.32)
. (3.32) . (3.33)
. (3.33)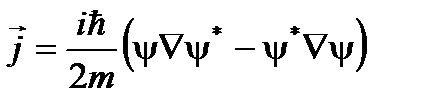 . (3.34)
. (3.34) . Поэтому
. Поэтому (3.35)
(3.35) , а
, а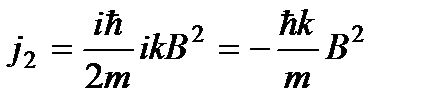 (3.36)
(3.36) (3.37)
(3.37)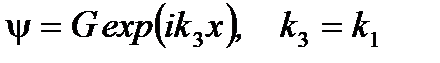 ):
): (3.38)
(3.38)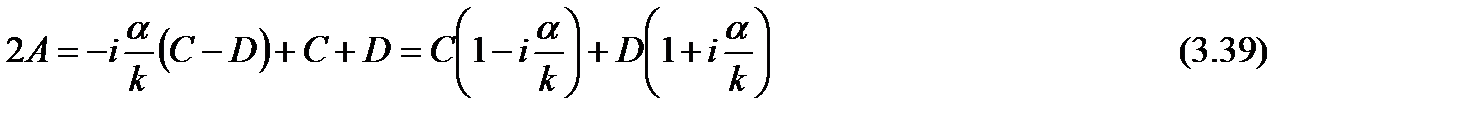








 . (3.40)
. (3.40) .
. . (3.41)
. (3.41) ,
,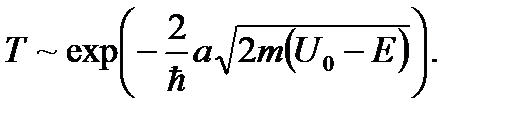
 . Подставляя решения системы уравнений (3.32) - (3.33), получаем
. Подставляя решения системы уравнений (3.32) - (3.33), получаем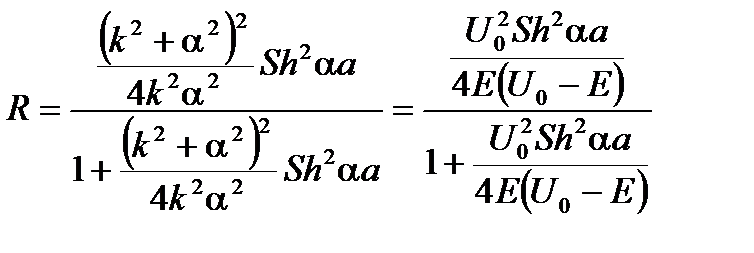 . (3.42)
. (3.42) . (3.43)
. (3.43) . В итоге мы получаем те же формулы для коэффициентов прохождения и отражения, только "a" меняем на " i a" и " Sh " на "- iSin ":
. В итоге мы получаем те же формулы для коэффициентов прохождения и отражения, только "a" меняем на " i a" и " Sh " на "- iSin ": , (3.44)
, (3.44)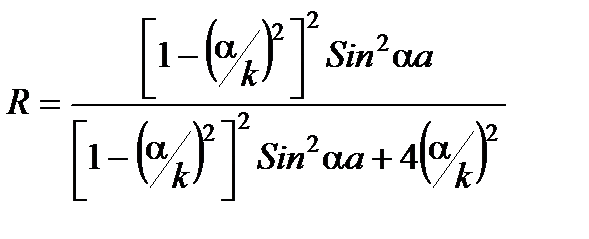 . (3.45)
. (3.45) (и
(и  ), т.е. частица может отразиться от барьера и при энергии, превышающей величину барьера, когда по классической механике частица проходит с достоверностью над барьером.
), т.е. частица может отразиться от барьера и при энергии, превышающей величину барьера, когда по классической механике частица проходит с достоверностью над барьером.
 (3.46)
(3.46) .
. медленно меняются на расстоянии ~ l. Это условие называется условием применения квазиклассического приближения. В самом деле, воспользуемся описанием изменения волновой функции при распространении частицы в пространстве с постоянным потенциалом, а именно:
медленно меняются на расстоянии ~ l. Это условие называется условием применения квазиклассического приближения. В самом деле, воспользуемся описанием изменения волновой функции при распространении частицы в пространстве с постоянным потенциалом, а именно:  , где p (x) = const (временной множитель
, где p (x) = const (временной множитель 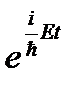 не существенен для определения координатной зависимости). Разбивая барьер на маленькие прямоугольные барьеры шириной D x, можно считать, что на ширине D x такого барьера U (x) = const и импульс частицы не меняется
не существенен для определения координатной зависимости). Разбивая барьер на маленькие прямоугольные барьеры шириной D x, можно считать, что на ширине D x такого барьера U (x) = const и импульс частицы не меняется  . Можно записать последовательность приближенного изменения волновой функции при переходе от одного барьера к другому:
. Можно записать последовательность приближенного изменения волновой функции при переходе от одного барьера к другому:

 ………
………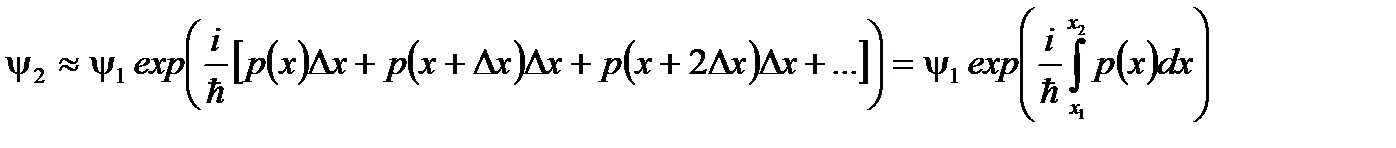 .
.
 . (3.47)
. (3.47) (5.18)
(5.18) . (5.19)
. (5.19) (5.20)
(5.20) , где
, где  .
. . (5.21)
. (5.21) (5.22)
(5.22) называются присоединенными полиномами Лежандра. Они cвязаны с полиномами Лежандра
называются присоединенными полиномами Лежандра. Они cвязаны с полиномами Лежандра  соотношением
соотношением (5.23)
(5.23) (5.24)
(5.24)
 , которые нормированы и ортогональны по индексам l и m, имеют вид:
, которые нормированы и ортогональны по индексам l и m, имеют вид:


 (5.25)
(5.25) нормировка радиальной функции учитывается в коэффициентах
нормировка радиальной функции учитывается в коэффициентах  . Для водородоподобного атома надо в этом выражении
. Для водородоподобного атома надо в этом выражении  заменить на
заменить на  .
. вырожден по числам
вырожден по числам  т.к. при заданном главном квантовом числе n орбитальное число
т.к. при заданном главном квантовом числе n орбитальное число  пробегает значения от нуля до n-1, а
пробегает значения от нуля до n-1, а  Кратность вырождения равна
Кратность вырождения равна (5.26)
(5.26) волновых функций.
волновых функций. . Поэтому, такое же соотношение выполняется и для операторов
. Поэтому, такое же соотношение выполняется и для операторов . (5.31)
. (5.31) называется гиромагнитным отношением.
называется гиромагнитным отношением. (5.32)
(5.32)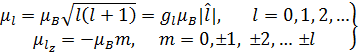 (5.33)
(5.33) = 0.927 ×10-20 эрг/Гс - элементарный квант магнитного момента. Для атома в (5.33) под
= 0.927 ×10-20 эрг/Гс - элементарный квант магнитного момента. Для атома в (5.33) под 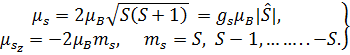 (5.34)
(5.34)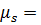

 Поэтому, принято говорить, что спиновый магнитный момент равен одному магнетону Бора.
Поэтому, принято говорить, что спиновый магнитный момент равен одному магнетону Бора. ). (5.35)
). (5.35)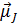 и вектор
и вектор  - неколлинеарные векторы. Чтобы найти гиромагнитное отношение этих векторов найдем проекции
- неколлинеарные векторы. Чтобы найти гиромагнитное отношение этих векторов найдем проекции  и
и  на направление вектора
на направление вектора  .
. . (5.36)
. (5.36) и
и  из (5.33) и (5.34), получаем
из (5.33) и (5.34), получаем =
=  .
. .(5.37)
.(5.37) (5.38)
(5.38) фактор Ланде
фактор Ланде  больше двух;
больше двух;
 =0, т.е. полный момент есть, а магнитного момента нет;
=0, т.е. полный момент есть, а магнитного момента нет; фактор Ланде
фактор Ланде 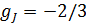 отрицателен, т.е. магнитный момент направлен в ту же сторону, что и полный момент количества движения.
отрицателен, т.е. магнитный момент направлен в ту же сторону, что и полный момент количества движения.



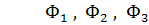 …
…



 без единой частицы называется истинным “вакуумом”. Совокупность всех функций
без единой частицы называется истинным “вакуумом”. Совокупность всех функций 
 (П1.3)
(П1.3) =
=  Пусть теперь эта система подверглась внешнему воздействию
Пусть теперь эта система подверглась внешнему воздействию  , в результате которого она перешла в состояние
, в результате которого она перешла в состояние  . Другими словами, действие оператора сводится в уничтожению частицы в одном состоянии и создании (рождении) частицы в другом. Чтобы описать все воздействия в системе, вводят два основных оператора: оператор уничтожения
. Другими словами, действие оператора сводится в уничтожению частицы в одном состоянии и создании (рождении) частицы в другом. Чтобы описать все воздействия в системе, вводят два основных оператора: оператор уничтожения  который уничтожает частицу в состоянии
который уничтожает частицу в состоянии  , и оператор рождения
, и оператор рождения  , который рождает частицу в состоянии
, который рождает частицу в состоянии 
 (П2.1)
(П2.1)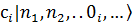 = 0,
= 0, 

 .
. “эрмитово сопряжены” друг с другом, т.е.
“эрмитово сопряжены” друг с другом, т.е. , (П2.2)
, (П2.2) ” соответствует эрмитову сопряжению. Отсюда следует, что сами операторы
” соответствует эрмитову сопряжению. Отсюда следует, что сами операторы  неэрмитовы и поэтому не отвечают наблюдаемым переменным. Легко показать, что оператор
неэрмитовы и поэтому не отвечают наблюдаемым переменным. Легко показать, что оператор  , который называется оператором числа частиц, является эрмитовым оператором. Оператор полного числа частиц
, который называется оператором числа частиц, является эрмитовым оператором. Оператор полного числа частиц  также эрмитов. В общем случае, из (П2.1) следует, что
также эрмитов. В общем случае, из (П2.1) следует, что (П2.3)
(П2.3) (П2.4)
(П2.4)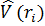 с матричными элементами
с матричными элементами
 =
=  . (П2.5)
. (П2.5)
 .
.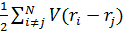 )
) , (П2.6)
, (П2.6) . (П2.7)
. (П2.7)


 , (П2.8)
, (П2.8)
 – собственные функции, и собственные значения одночастичного оператора
– собственные функции, и собственные значения одночастичного оператора  .
. для решения уравнения Шредингера с гамильтонианом (П2.8) приходится прибегать к целому ряду приближений, вводя модельные гамильтонианы. В твердом теле важнейшими модельными гамильтонианами являются:
для решения уравнения Шредингера с гамильтонианом (П2.8) приходится прибегать к целому ряду приближений, вводя модельные гамильтонианы. В твердом теле важнейшими модельными гамильтонианами являются: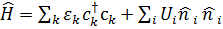 , (П2.9)
, (П2.9) . (П2.10)
. (П2.10) - параметры обменного взаимодействия Гейзенберга между атомными спинами
- параметры обменного взаимодействия Гейзенберга между атомными спинами  и
и 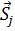 .
.


