
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одномерная потенциальная яма с конечными стенкамиСодержание книги
Поиск на нашем сайте
Рис.3.2. Одномерная прямоугольная яма со стенками конечной высоты. Выберем начало координат на дне ямы симметрично относительно стенок:
Найдем сначала решения уравнения Шредингера внутри и вне ямы. Для получения общего решения необходимо “сшить” эти решения на границе ямы. При энергии частицы E > U 0 имеем непрерывный спектр энергий, частица пролетает над ямой и может иметь любую энергию. В самом деле, внутри ямы имеем уравнение Рассмотрим подробнее случай, когда энергия частицы E < U 0. В этом случае мы получаем дискретный спектр связанных состояний. Для двух областей: | x | < a /2 | x | > a /2 Введем оператор четности с помощью соотношения
Из (3.15) следует, что все собственные функции гамильтониана имеют определенную четность. Рассмотрим эти состояния поочередно. Нечетные состояния. Запишем решения уравнений (3.13) и (3.14) для нечетных состояний
Рис.3.3. Схематический вид нечетной волновой функции в прямоугольной яме конечной глубины.
На Рис.3.3. показано, что частица проникает вне области ямы, при этом глубина проникновения частицы под барьер Из условий непрерывности волновой функции и её производной на границе x = a /2 следует:
Делением верхнего уравнения на нижнее уравнение получаем, что
Это трансцендентное уравнение определяет энергии разрешенных состояний. То же самое уравнение получим в силу симметрии из граничного условия при x = - a /2. Введем обозначение
где введен параметр мощности ямы:
Для определения спектра надо решить трансцендентное уравнение
Рассмотрим решение этого уравнения графически, для чего построим отдельно правую и левую части уравнения. Точки пересечения дают корни этого уравнения. Из рисунка видно, что решения имеются не при всех t. Чем больше мощность ямы t, тем больше корней уравнения - больше уровней энергии. При уменьшении t число корней уменьшается. А при мощности
корней соответствующих нечетным состояниям нет вовсе. Напомним, что t 0 = 0 и E 0 = 0 не являются корнями, т.к. при этом решение внутри ямы есть
Рис.3.4. Графическое нахождение собственных энергий нечетных состояний.
Итак, для нечетных состояний, получаем: - при мощности ямы - при мощности ямы - при мощности ямы Четные состояния. Запишем теперь решения для четных состояний:
На границе ямы при x = a /2 имеем:
Откуда получаем новое трансцендентное уравнение
В силу симметрии то же уравнение дают граничные условия при x = - a /2. Из графического решения этого уравнения видно, что при всех возможных значениях параметра t хоть одно решение есть всегда. Чем больше t, тем больше четных решений.
Рис.3.4. Графическое нахождение собственных энергий четных состояний.
Итак, при мощности ямы Рассмотрим теперь “мелкую” яму, для которой t << 1. Для такой ямы достаточно легко найти энергию единственного четного состояния (t £ t << 1). Из (3.23) следует, что
а для энергии
Первый (четный) уровень энергии находится теперь у самого “верха” ямы. В одномерной яме с конечными стенками всегда существует хотя бы одно связанное состояние. При малой глубине и ширине (мощности) ямы в яме имеется только один четный уровень. С ростом U 0 и a растет мощность ямы, и появляются новые уровни при прохождении параметром t значений
Рис.3.5. Качественное поведение волновых функции низших состояний.
В одномерной потенциальной яме хотя бы один уровень существует всегда, но это не так в трехмерной потенциальной яме. Для нее существование хотя бы одного уровня зависит от “мощности” потенциальной ямы:
Потенциальные барьеры
 . Если на каком-то участке координаты x потенциальная энергия возрастает (или падает), то говорят об одномерной потенциальной ступеньке. . Если на каком-то участке координаты x потенциальная энергия возрастает (или падает), то говорят об одномерной потенциальной ступеньке.
Рассмотрим задачу, когда на одномерную потенциальную ступеньку налетает частица. Если выполняется условие, что размер области изменения потенциальной энергии D x мал по сравнению с волной де Бройля частицы В классическом случае, если энергия налетающей частицы E < U 0, то частица с достоверностью отражается и в правую область не проникает. Если ее энергия E > U 0, тогда частица с достоверностью проходит над барьером и в правой области она движется с меньшей скоростью Прямоугольный потенциальный барьер. Пусть на прямоугольный потенциальный барьер (Рис.3.6) слева падает поток частиц с полной энергией
Рис.3.6. Прохождение частицы сквозь прямоугольный потенциальный барьер.
Потенциальная энергия
Разобьем пространство на три части I, II и III. В I и III областях имеем уравнение Шредингера для свободной частицы:
Его решения: I область III область Во II области имеем:
Соответствующее решение под барьером
Волна exp (ikx) движется в положительном направлении оси x, а волна exp (- ikx) - в обратном. В III области не будет волны в обратном направлении оси x, т.к. из бесконечности нет потока частиц. Окончательно
На границах полная волновая функция и ее первая производная непрерывны. Эти граничные условия дают систему уравнений для определения коэффициентов A, B, C, D и G. При x = 0
При x = a Введем коэффициенты отражения и прохождениякак отношение плотностей потока
В I области поток вправо определяется волной, распространяющейся вдоль оси x,
Поток влево в I области определяется волной
Коэффициент отражения определяется
Коэффициент прохождения (поток пройденной волны определяется волной
В первой паре уравнений (3.32) сложим два уравнения, избавляясь от коэффициента В.
Во второй паре уравнений (3.33) делим на a второе уравнение, затем складывая и вычитая, получаем следующие два соотношения:
Выражая отсюда 2 С и 2 D и подставляя их в предыдущее уравнение, имеем
Раскрывая скобки, получаем
Введем гиперболический косинус и гиперболический синус:
Для них выполняется теорема Пифагора Тогда:
Теперь, раскрывая скобки и учитывая теорему Пифагора, получаем для отношения квадратов:
Здесь Результирующее выражение для коэффициента прохождения имеет вид
Исследование коэффициентов прохождения и отражения. То, что коэффициент прохождения не равен нулю при полной энергии частицы меньшей потенциального барьера E < U 0 – называется туннельным эффектом. В классической физике ничего подобного нет, туннельный эффект – чисто квантовый эффект. При условии a a >> 1 можно получить для коэффициента прохождения Т:
или Коэффициент отражения определяется соотношением
Как и должно быть из закона сохранения вероятности
Случай E > U 0. Решение получается тем же путем, как и ранее, только в области II имеем решение, описывающее движение свободной частицы с
В общем случае мы имеем коэффициент отражения не равный нулю Однако, есть характерные энергии, когда коэффициент отражения равен 0, а коэффициент прохождения равен 1:
При таких энергиях частица пролетает над барьером с достоверностью и при квантовом рассмотрении. Заметим, что при этом целое число полуволн де Бройля укладывается на барьере, чему соответствует условие Аналогичное решение для коэффициентов прохождения и отражения получаем для барьера в виде прямоугольной ямы, при этом меняется только " U 0" на "- U 0". Отметим, что в общем случае коэффициент отражения не равен нулю. Коэффициент прохождения обращается в единицу только для таких энергий когда на размере ямы укладывается целое число полуволн де Бройля. Барьер произвольной формы.
Рис.3.7. Прохождение частицы сквозь потенциальный барьер произвольной формы.
Приближенно задачу можно решить, если барьеры достаточно широкие, и при этом импульс p (x) и соответствующая волна де Бройля
Тогда связь волновой функции на выходе из барьера с волновой функцией на входе записывается, как
Коэффициент прохождения через барьер произвольной формы
Здесь мы поменяли местами потенциальную и полную энергии частицы. В итоге
Выражение (3.47) позволяет найти коэффициент прохождения через барьер произвольной формы в квазиклассическом приближении.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

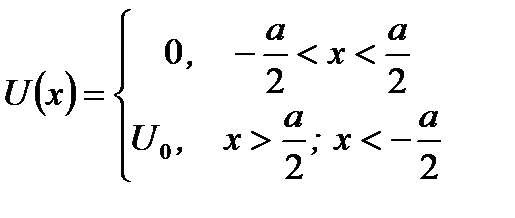 (3.12)
(3.12)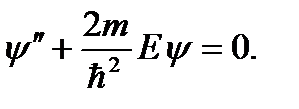 Вводя
Вводя 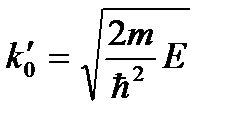 , записываем решение в этой области
, записываем решение в этой области  Вне ямы имеем уравнение
Вне ямы имеем уравнение  Вводя волновое число
Вводя волновое число 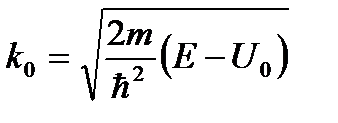 , получаем решение вне ямы
, получаем решение вне ямы  . Сшивая эти решения на границе, получаем, что любые энергии частицы разрешены. Таким образом, имеем сплошной спектр при E > U 0.
. Сшивая эти решения на границе, получаем, что любые энергии частицы разрешены. Таким образом, имеем сплошной спектр при E > U 0.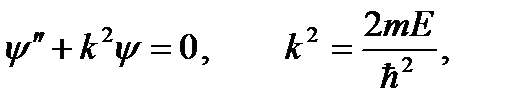 (3.13)
(3.13) (3.14)
(3.14) . Собственные числа оператора четности могут быть получены, если повторно подействовать им на исходную волновую функцию. Тогда получаем, что
. Собственные числа оператора четности могут быть получены, если повторно подействовать им на исходную волновую функцию. Тогда получаем, что 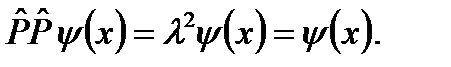 Таким образом, значения собственных чисел l = ±1. Для значения l = 1, получаем “четное” состояние, а для l = -1, имеем “нечетное” состояние. Поскольку
Таким образом, значения собственных чисел l = ±1. Для значения l = 1, получаем “четное” состояние, а для l = -1, имеем “нечетное” состояние. Поскольку  , то оператор четности коммутирует с гамильтонианом рассматриваемой задачи
, то оператор четности коммутирует с гамильтонианом рассматриваемой задачи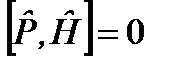 . (3.15)
. (3.15) (3.16)
(3.16) .
. (3.17)
(3.17)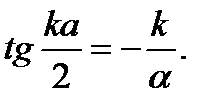 (3.18)
(3.18) , тогда для правой части (3.18) получаем
, тогда для правой части (3.18) получаем ,
, . (3.19)
. (3.19) . (3.20)
. (3.20)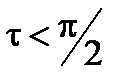 , т.е. при
, т.е. при ,
, , которое не удовлетворяет граничным условиям.
, которое не удовлетворяет граничным условиям.
 нет дискретных состояний;
нет дискретных состояний; существует 1 нечетное состояние;
существует 1 нечетное состояние;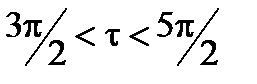 существует 2 нечетных состояний и т.д.
существует 2 нечетных состояний и т.д. (3.21)
(3.21) (3.22)
(3.22) или
или 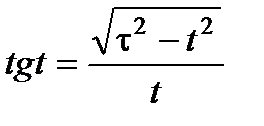 . (3.23)
. (3.23)
 получаем одно четное решение, при мощности
получаем одно четное решение, при мощности 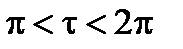 получаем два четных решения и т.д.
получаем два четных решения и т.д. Решая это уравнение, получаем
Решая это уравнение, получаем Вспоминая, что
Вспоминая, что 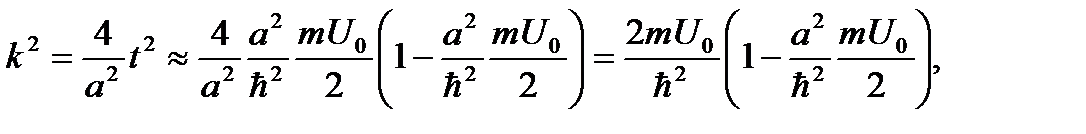
 (3.24)
(3.24) , где n – целое число. Четные и нечетные уровни появляются по очереди, причем вначале четные. Качественное поведение волновых функции низших состояний показано на Рис.3.5. Возводя в квадрат эти волновые функции, получаем плотность вероятности нахождения частицы при данной координате.
, где n – целое число. Четные и нечетные уровни появляются по очереди, причем вначале четные. Качественное поведение волновых функции низших состояний показано на Рис.3.5. Возводя в квадрат эти волновые функции, получаем плотность вероятности нахождения частицы при данной координате. , где U 0 – глубина ямы, а a – ее размер. При малых мощностях ямы энергия частицы тоже должна быть малой, т.е. частица имеет большую волну де Бройля, и она как бы не “помещается” внутри ямы.
, где U 0 – глубина ямы, а a – ее размер. При малых мощностях ямы энергия частицы тоже должна быть малой, т.е. частица имеет большую волну де Бройля, и она как бы не “помещается” внутри ямы. , то тогда можно считать барьер прямоугольным, для которого
, то тогда можно считать барьер прямоугольным, для которого  .
. . В рамках квантово-механического рассмотрения решается уравнение Шредингера в области до порога x < 0 и после порога x > 0, а затем решения “сшиваются” на границе (x = 0).
. В рамках квантово-механического рассмотрения решается уравнение Шредингера в области до порога x < 0 и после порога x > 0, а затем решения “сшиваются” на границе (x = 0). , меньшей величины барьера.
, меньшей величины барьера. (3.25)
(3.25) . (3.26)
. (3.26)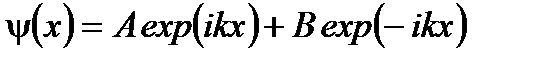 , (3.27)
, (3.27) . (3.28)
. (3.28) . (3.29)
. (3.29) (3.30)
(3.30) . (3.31)
. (3.31) . (3.32)
. (3.32) . (3.33)
. (3.33)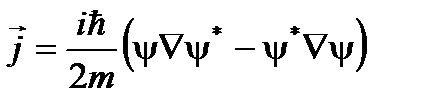 . (3.34)
. (3.34) . Поэтому
. Поэтому (3.35)
(3.35) , а
, а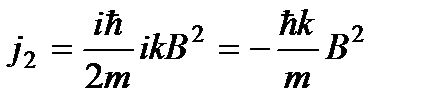 (3.36)
(3.36) (3.37)
(3.37)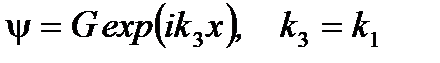 ):
): (3.38)
(3.38)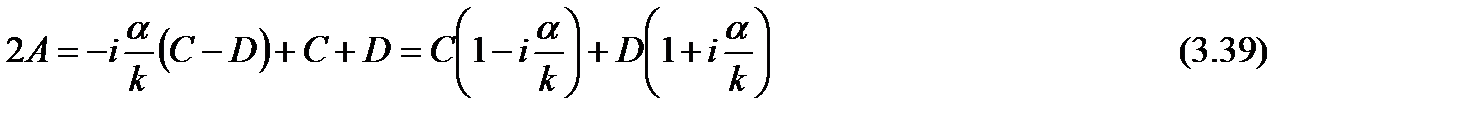








 . (3.40)
. (3.40) .
. . (3.41)
. (3.41) ,
,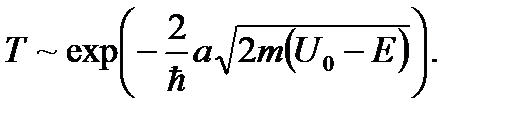
 . Подставляя решения системы уравнений (3.32) - (3.33), получаем
. Подставляя решения системы уравнений (3.32) - (3.33), получаем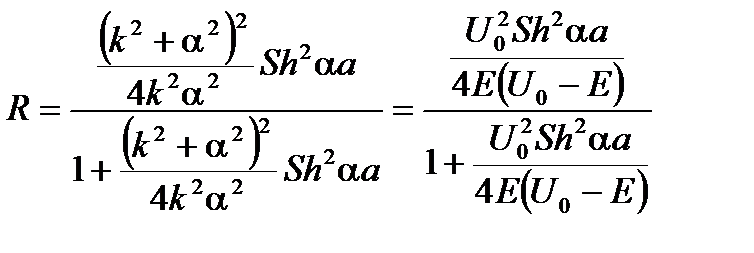 . (3.42)
. (3.42) . (3.43)
. (3.43) . В итоге мы получаем те же формулы для коэффициентов прохождения и отражения, только "a" меняем на " i a" и " Sh " на "- iSin ":
. В итоге мы получаем те же формулы для коэффициентов прохождения и отражения, только "a" меняем на " i a" и " Sh " на "- iSin ": , (3.44)
, (3.44)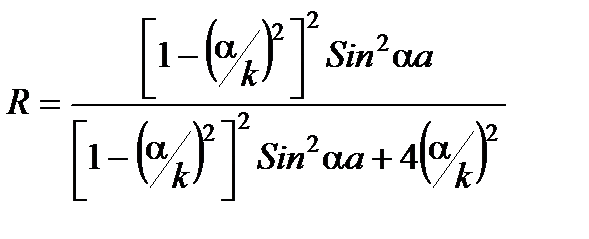 . (3.45)
. (3.45) (и
(и  ), т.е. частица может отразиться от барьера и при энергии, превышающей величину барьера, когда по классической механике частица проходит с достоверностью над барьером.
), т.е. частица может отразиться от барьера и при энергии, превышающей величину барьера, когда по классической механике частица проходит с достоверностью над барьером.
 (3.46)
(3.46) .
. медленно меняются на расстоянии ~ l. Это условие называется условием применения квазиклассического приближения. В самом деле, воспользуемся описанием изменения волновой функции при распространении частицы в пространстве с постоянным потенциалом, а именно:
медленно меняются на расстоянии ~ l. Это условие называется условием применения квазиклассического приближения. В самом деле, воспользуемся описанием изменения волновой функции при распространении частицы в пространстве с постоянным потенциалом, а именно:  , где p (x) = const (временной множитель
, где p (x) = const (временной множитель 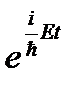 не существенен для определения координатной зависимости). Разбивая барьер на маленькие прямоугольные барьеры шириной D x, можно считать, что на ширине D x такого барьера U (x) = const и импульс частицы не меняется
не существенен для определения координатной зависимости). Разбивая барьер на маленькие прямоугольные барьеры шириной D x, можно считать, что на ширине D x такого барьера U (x) = const и импульс частицы не меняется  . Можно записать последовательность приближенного изменения волновой функции при переходе от одного барьера к другому:
. Можно записать последовательность приближенного изменения волновой функции при переходе от одного барьера к другому:

 ………
………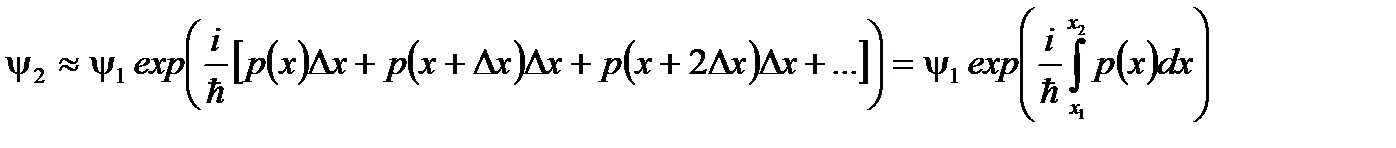 .
.
 . (3.47)
. (3.47)


