
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Состояние электронов в атоме. Спин электронаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Атом с более чем одним электроном представляет собой сложную систему взаимодействующих друг с другом электронов. Тем не менее, можно ввести понятие о стационарных состояниях отдельного электрона, движущегося в некотором центрально-симметричном потенциальном поле, создаваемым остальными электронами. Такое поле называется самосогласованным. Поскольку это поле центрально - симметрично, то состояния электронов в этом поле можно характеризовать значением его орбитального момента Спин электрона. Учтем теперь, что каждый электрон обладает собственным моментом количества движения В общем случае вводится полный момент импульса частицы (вектор)
который складывается из орбитального момента
где (2S+1) где L –символ состояния, соответствующий полному орбитальному моменту: L = 0 1 2 3 4 5 6 7 8 9 10 1, S =1/2, J =3/2. Электронные конфигурации теперь записываются в виде 1s22s22p63d3 и т.п. Для квантового числа j действует правило отбора, согласно которому переходы между уровнями возможны только при выполнении условия
Правила Хунда. Для определения, какой терм отвечает минимуму энергии электронов, находящихся в одной подоболочке, существуют полуэмпирические правила Хунда. Первое правило - минимальной энергией данной электронной конфигурации обладает терм с наибольшим полным спином S и с наибольшим (для этого S) значением L. Второе правило – J = | L-S |, если оболочка заполнена менее, чем наполовину, и J = L+S во всех остальных случаях. Рассмотрим, например, конфигурацию 3d6. Для неё l =2. Максимальная сумма проекций спина
Магнитный момент атома Из курса общей физики известно, что магнитный и орбитальный моменты электрона связаны соотношением
Знак минус показывает, что магнитный и орбитальный моменты электрона направлены в противоположные стороны. Отношение магнитного момента к орбитальному Из релятивистской теории Дирака и эксперимента следует, что для что магнитного и спинового моментов электрона имеет место соотношение
в котором коэффициент пропорциональности в два раза, чем в выражении (5.31). Иначе говоря, спин обладает удвоенным магнетизмом. В стационарном состоянии определенны значения могут иметь только модуль магнитного момента и его проекция на выделенную ось:
Мы ввели в (5.33) магнетон Бора Для атомного спина:
При S=1/2 ms =1/2, -1/2, Полный магнитный момент атома. Рассмотрим
Отсюда следует, что вектор полного магнитного момента
В силу (5.35)
Подставляя сюда явные выражения для
Сравнивая это выражение с (5.36), получаем фактор Ланде
Теперь
Отметим ряд наиболее интересных случаев: · в состоянии 5 · в состоянии 4 · в состоянии 6
Глава 6. Теория возмущений
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

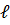 . При заданном
. При заданном  Состояния отдельных электронов с различными n и
Состояния отдельных электронов с различными n и 
 , названного спином. Спин – такое же внутреннее свойство электрона, как масса и заряд. Это квантовая величина, не имеющая классического аналога. Он не имеет ничего общего с вращением в реальном пространстве. Экспериментально установлено, что: для электрона s=1/2, т.е.
, названного спином. Спин – такое же внутреннее свойство электрона, как масса и заряд. Это квантовая величина, не имеющая классического аналога. Он не имеет ничего общего с вращением в реальном пространстве. Экспериментально установлено, что: для электрона s=1/2, т.е.  ; для протона и нейтрона s=1/2; для фотона s=1. С учетом спина кратность вырождения энергетических уровней атома водорода равна
; для протона и нейтрона s=1/2; для фотона s=1. С учетом спина кратность вырождения энергетических уровней атома водорода равна  , а не
, а не  .
. , (5.27)
, (5.27) и спина
и спина  + s-1,… |
+ s-1,… |  , то j =1/2. Это правило следует из правила сложения любых двух операторов момента импульса
, то j =1/2. Это правило следует из правила сложения любых двух операторов момента импульса  (без вывода). Для системы частиц (в схеме Рассела - Саундерса)
(без вывода). Для системы частиц (в схеме Рассела - Саундерса) (5.28)
(5.28) - полный орбитальный момент,
- полный орбитальный момент, 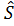 - полный спин системы. Операторы спина и полного момента удовлетворяют тем же правилам коммутации, что и операторы орбитального момента. В первом приближении можно считать абсолютные значения орбитального момента L и спина S (но не направления) сохраняющимися и характеризовать с их помощью уровни энергии. В результате релятивистских эффектов уровень с фиксированными значениями L и S расщепляется на ряд подуровней различными значениями J. Возникает тонкая структура (мультиплетное расщепление) уровня. Число J пробегает значения от L+S до |L-S|. Атомные уровни энергии (спектральные термы) принято обозначать символами
- полный спин системы. Операторы спина и полного момента удовлетворяют тем же правилам коммутации, что и операторы орбитального момента. В первом приближении можно считать абсолютные значения орбитального момента L и спина S (но не направления) сохраняющимися и характеризовать с их помощью уровни энергии. В результате релятивистских эффектов уровень с фиксированными значениями L и S расщепляется на ряд подуровней различными значениями J. Возникает тонкая структура (мультиплетное расщепление) уровня. Число J пробегает значения от L+S до |L-S|. Атомные уровни энергии (спектральные термы) принято обозначать символами , (5.29)
, (5.29) (5.30)
(5.30) 2, значит S
2, значит S  . Максимальное значение проекций орбитального момента шести электронов L =2. Так как оболочка заполнена более, чем наполовину, то J = L + S, и основным термом будет 5
. Максимальное значение проекций орбитального момента шести электронов L =2. Так как оболочка заполнена более, чем наполовину, то J = L + S, и основным термом будет 5 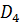 .
. . Поэтому, такое же соотношение выполняется и для операторов
. Поэтому, такое же соотношение выполняется и для операторов . (5.31)
. (5.31) называется гиромагнитным отношением.
называется гиромагнитным отношением. (5.32)
(5.32)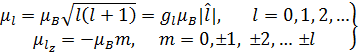 (5.33)
(5.33) = 0.927 ×10-20 эрг/Гс - элементарный квант магнитного момента. Для атома в (5.33) под
= 0.927 ×10-20 эрг/Гс - элементарный квант магнитного момента. Для атома в (5.33) под  надо понимать L.
надо понимать L.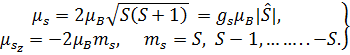 (5.34)
(5.34)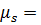

 Поэтому, принято говорить, что спиновый магнитный момент равен одному магнетону Бора.
Поэтому, принято говорить, что спиновый магнитный момент равен одному магнетону Бора. ). (5.35)
). (5.35)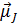 и вектор
и вектор  - неколлинеарные векторы. Чтобы найти гиромагнитное отношение этих векторов найдем проекции
- неколлинеарные векторы. Чтобы найти гиромагнитное отношение этих векторов найдем проекции  и
и  на направление вектора
на направление вектора  .
. . (5.36)
. (5.36) и
и  из (5.33) и (5.34), получаем
из (5.33) и (5.34), получаем =
=  .
. .(5.37)
.(5.37) (5.38)
(5.38) фактор Ланде
фактор Ланде  больше двух;
больше двух;
 =0, т.е. полный момент есть, а магнитного момента нет;
=0, т.е. полный момент есть, а магнитного момента нет; фактор Ланде
фактор Ланде 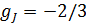 отрицателен, т.е. магнитный момент направлен в ту же сторону, что и полный момент количества движения.
отрицателен, т.е. магнитный момент направлен в ту же сторону, что и полный момент количества движения.


