
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самосопряженные (эрмитовы) операторы и их свойстваСодержание книги
Поиск на нашем сайте
Непосредственно измеряемые (“наблюдаемые”) физические величины вещественны, т.е. все собственные значения оператора 1) если физическая система (частица) находится в состоянии, описываемом собственной функцией 2) если система (частица) описывается произвольной функцией Введем понятие транспонированного оператора
т.е. транспонированный оператор дает тот же результат, действуя на левую функцию, что и оператор Самосопряженные операторы определяются следующим равенством
где Если
то этот оператор называется эрмитовым или самосопряженным оператором. Можно сказать, что действие оператора
Таким образом, сопряженный оператор – это комплексно сопряженный оператор от транспонированного оператора
Рассмотрим оператор дифференцирования
Таким образом, оператор, сопряженный оператору и, следовательно, оператор оператор импульса
Оператор координаты Рассмотрим уравнения
Данное равенство означает, что собственные значения эрмитова оператора в ещественны. Произведение двух эрмитовых коммутирующих операторов есть эрмитов оператор
Пусть мы имеем дискретный набор собственных значений и собственных функций эрмитова оператора
В математике строго доказано, что набор собственных волновых функций эрмитова оператора образует полную систему ортонормированных волновых функций, т.е.
В самом деле, для доказательства ортогональности рассмотрим два равенства
Умножим слева первое уравнение на
Отсюда следует, что если l n ¹ l m, то В случае, когда имеем вырождение, волновая функция берется в виде линейной комбинации Рассмотрим разложение произвольной функции в ряд по системе собственных функций самосопряженного линейного оператора
Коэффициенты разложения можно получить, умножив обе части выражения на
Таким образом,
Квадрат коэффициента | Если имеем непрерывный спектр значений, тогда волновую функцию раскладываем в интеграл
где коэффициенты определяются
Волновые функции непрерывного спектра нормируются на d -функцию
Свойства d- функции. Функция
Геометрически d-функцию можно рассматривать как предел максимума, стремящегося к бесконечности в точке a и сохраняющего площадь под кривой равной единице. Важное свойство d- функции состоит в том, что она “вырезает” из функции в подынтегральном выражении значение этой функции в точке a
Последнее условие и нормировка позволяет получать коэффициенты
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.112.44 (0.008 с.) |

 - { gn } должны быть вещественны. В результате измерения физической величины, описываемой оператором
- { gn } должны быть вещественны. В результате измерения физической величины, описываемой оператором 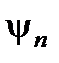 , то при измерении получим соответствующее собственное значение gn;
, то при измерении получим соответствующее собственное значение gn; , то при измерении наблюдаемой, т.е. действии оператора
, то при измерении наблюдаемой, т.е. действии оператора  , который определяется из соотношения
, который определяется из соотношения , (2.34)
, (2.34) , действуя на правую.
, действуя на правую.
 - оператор, сопряженный к оператору
- оператор, сопряженный к оператору 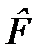 .
. (2.36)
(2.36)

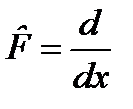 . Будем считать, что волновые функции равны нулю на бесконечности. Вычислим оператор, сопряженный оператору
. Будем считать, что волновые функции равны нулю на бесконечности. Вычислим оператор, сопряженный оператору  с помощью интегрирования по частям:
с помощью интегрирования по частям: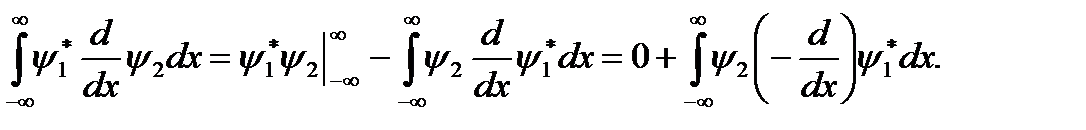

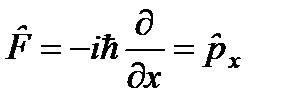 - самосопряженный оператор.
- самосопряженный оператор.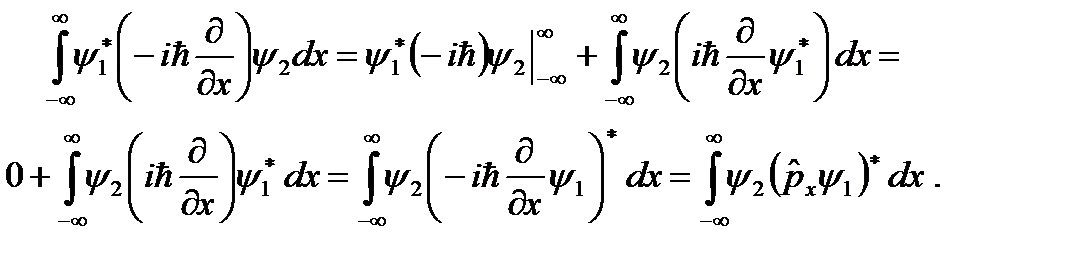
 также эрмитов оператор.
также эрмитов оператор. и
и 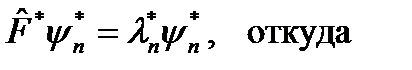
 (2.39)
(2.39)
 разные для разных собственных значений
разные для разных собственных значений  ):
):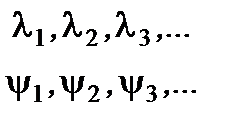


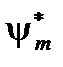 , второе на
, второе на  , и проинтегрируем. Вычитая второе уравнение из первого уравнения и учитывая, что (
, и проинтегрируем. Вычитая второе уравнение из первого уравнения и учитывая, что ( - эрмитов оператор)
- эрмитов оператор)  , получаем:
, получаем: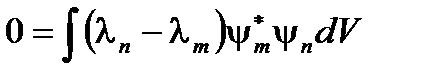 ,
,
 . Полнота набора означает, что любую функцию можно разложить в ряд по функциям
. Полнота набора означает, что любую функцию можно разложить в ряд по функциям  .
. , где все волновые функции имеют одно и то же собственное значение
, где все волновые функции имеют одно и то же собственное значение 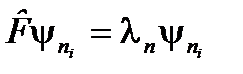 . При этом линейные комбинации можно сделать такими, что новые волновые функции будут ортонормированными.
. При этом линейные комбинации можно сделать такими, что новые волновые функции будут ортонормированными.
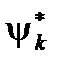 и интегрируя:
и интегрируя:

 | дает вероятность того, что в состоянии, описываемом
| дает вероятность того, что в состоянии, описываемом 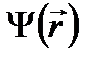 , присутствует примесь состояния
, присутствует примесь состояния 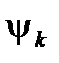 .
.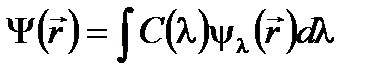 , (2.47)
, (2.47)

 везде равна нулю за исключением точки x = a, где она обращается в бесконечность:
везде равна нулю за исключением точки x = a, где она обращается в бесконечность: или
или 
 или
или 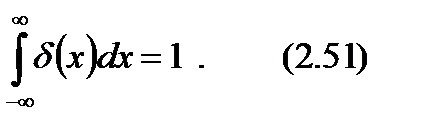

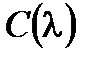 .
.


