
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнения Шредингера одномерного осциллятора при помощи операторов рождения и уничтоженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Существует более простой и современный метод решения уравнения Шредингера гармонического осциллятора, основанный на представлениях об операторах рождения и уничтожения. Кроме того, в этом параграфе воспользуемся формализмом Дирака.
Введем операторы:
Прямым вычислением легко показать, что их коммутатор
[
Гамильтониан одномерного квантового осциллятора записывается с помощью этих операторов в виде
Удобно определять в дальнейшем энергию в единицах
 - нормированное собственное состояние с энергией - нормированное собственное состояние с энергией
En = n+1/2, т.е.
Тогда
Таким образом, действие оператора Интерпретация: состояние Заметим, что собственные значения оператора
равны n, поэтому
Таким образом, нормированное состояние
Отличные от нуля матричные элементы операторов рождения и уничтожения равны
Прямым вычислением легко показать, что
Как уже отмечалось, волновая функция основного состояния
Это сразу же дает
Для волновой функции с n >0получаем компактное выражение
Очевидно, что эти состояния (волновые функции) ортонормированны. Это легко показать, используя соотношения коммутации (3.69) и условие (3.79).
Квантовый осциллятор в электрическом поле. Гамильтониан одномерного осциллятора в электрическом поле F, направленном вдоль оси х, имеет вид
где Введём операторы
Все коммутационные соотношения для новых операторов совпадают с коммутационными соотношениями для операторов
где
Рассмотрим оператор координаты
В отсутствии поля все малые колебания происходят вокруг
Глава 4. Момент импульса Момент импульса в квантовой механике Оператор момента импульса
где проекции оператора момента импульса:
Вычислим коммутатор двух проекций момента импульса, используя известное нам соотношение коммутации
Для остальных проекций момента импульса получаем:
Так как коммутаторы в (4.5) отличны от нуля, то две любые проекции момента импульса не могут одновременно иметь определенные значения. Следовательно, и вектор момента импульса
Здесь
В терминах этих операторов квадрат момента импульса
Из (4.8) и (4.7) сразу же следует, что
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.45.11 (0.009 с.) |



 ,
,  . (3.68)
. (3.68) ]=1. (3.69)
]=1. (3.69) . (3.70)
. (3.70) тогда
тогда  . Используя (3.69), нетрудно показать, что
. Используя (3.69), нетрудно показать, что . (3.71)
. (3.71)
 . (3.72)
. (3.72) и
и  - собственные состояния (ненормированные) с энергией
- собственные состояния (ненормированные) с энергией  +1 и
+1 и  1 соответственно. Действительно,
1 соответственно. Действительно, , (3.73)
, (3.73) . (3.74)
. (3.74) на состояние
на состояние  , то есть повышает энергию состояния на единицу,
, то есть повышает энергию состояния на единицу,  , а действие оператора a на состояние
, а действие оператора a на состояние  переводит его в состояние
переводит его в состояние 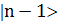 , то есть понижает энергию состояния на единицу.
, то есть понижает энергию состояния на единицу. каждая. Оператор
каждая. Оператор  называют повышающим оператором или оператором рождения такой частицы, а оператор
называют повышающим оператором или оператором рождения такой частицы, а оператор  - понижающим оператором или оператором уничтожения. Состояние
- понижающим оператором или оператором уничтожения. Состояние  , соответствующее условию n=0 (отсутствию возбуждений) называется основным состоянием. Понизить энергию этого состояния нельзя, поэтому это состояние должно удовлетворять уравнению
, соответствующее условию n=0 (отсутствию возбуждений) называется основным состоянием. Понизить энергию этого состояния нельзя, поэтому это состояние должно удовлетворять уравнению  .
. (3.75)
(3.75) называют оператором числа частиц. Найдем коэффициент cn. Для этого вычислим норму вектора
называют оператором числа частиц. Найдем коэффициент cn. Для этого вычислим норму вектора  :
: =
=  . (3.76)
. (3.76) . (3.77)
. (3.77) . (3.78)
. (3.78)
 ,
,  ,
, .
. может быть найдена из условия
может быть найдена из условия . (3.80)
. (3.80) . (3.81)
. (3.81) (3.82)
(3.82) .
. , тогда
, тогда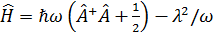 . (3.83)
. (3.83) и
и 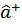 . Очевидно, что
. Очевидно, что , (3.84)
, (3.84)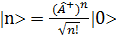 . (3.85)
. (3.85) . (3.86)
. (3.86) . Электрическое поле просто сдвигает положение
. Электрическое поле просто сдвигает положение  из нуля в точку
из нуля в точку  .
. (4.1)
(4.1) , (4.2)
, (4.2) (4.3)
(4.3)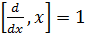 :
: (4.4)
(4.4) (4.5)
(4.5) не имеет определенного направления в пространстве. Кроме соотношения (4.5), выполняются следующие правила коммутации, которые в сжатом виде можно представить, как (
не имеет определенного направления в пространстве. Кроме соотношения (4.5), выполняются следующие правила коммутации, которые в сжатом виде можно представить, как ( ):
): ,
,  (4.6)
(4.6) – единичный псевдотензор третьего ранга. Он равен нулю, если любая пара индексов совпадает, равен единице в случае
– единичный псевдотензор третьего ранга. Он равен нулю, если любая пара индексов совпадает, равен единице в случае  и меняет знак при перестановке соседних индексов
и меняет знак при перестановке соседних индексов  Рассмотрим теперь более подробно оператор
Рассмотрим теперь более подробно оператор  . Введём операторы
. Введём операторы 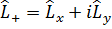 ,
,  , для которых имеют место соотношения:
, для которых имеют место соотношения: ,
, 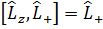 ,
,  . (4.7)
. (4.7) (4.8)
(4.8) . Таким образом, в квантовой механике векторная величина момента импульса не может иметь определенного значения. Определенное значение имеют одновременно абсолютная величина момента импульса (квадрат момента импульса сохраняется) и одна из его проекций, которая не может совпадать с модулем
. Таким образом, в квантовой механике векторная величина момента импульса не может иметь определенного значения. Определенное значение имеют одновременно абсолютная величина момента импульса (квадрат момента импульса сохраняется) и одна из его проекций, которая не может совпадать с модулем 



