
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекции по квантовой механике и статистической физикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» им. В.И.Ульянова (Ленина) С.М.Дунаевский ЛЕКЦИИ ПО КВАНТОВОЙ МЕХАНИКЕ И СТАТИСТИЧЕСКОЙ ФИЗИКЕ СТАТИСТИЧЕСКАЯ ФИЗИКА
Учебное пособие
Санкт-Петербург
Печатается по решению издательского совета факультета электроники.
С.М.Дунаевский Лекции квантовой механике и статистической физике. Статистическая физика. Учебное пособие. Данное пособие представляет собой вторую часть расширенного конспекта лекций по курсу квантовой механики и статистической физики, который читается в весеннем семестре студентам третьего курса факультета электроники Санкт-Петербургского Государственного Электротехнического Университета (“ЛЭТИ”) им. В. И. Ульянова (Ленина). В пособии изложены основные законы и приведены выводы необходимых формул классической и квантовой статистической физики.
ОГЛАВЛЕНИЕ
Глава1. Статистические распределения. §1.1. Введение. Термодинамический и статистический подходы. §. 1.2.Основные понятия теории вероятностей. §.1.3. Среднее значение случайных величин. Флуктуации. §1.4.Биномиальное распределение молекул в объеме. §1.5. Статистическое распределение. Квазизамкнутость. §1.6.Фазовое пространство. Функция распределения. §1.7. Функция распределения по энергиям. §1.8.Энтропия. Глава 2. Распределение Гиббса. §2.1.Канонический ансамбль. Распределение Гиббса. §2.2.Распределение Максвелла и его свойства. §2.3. Распределение Больцмана и его свойства. Статистическое равновесие. Если замкнутая макросистема находится в состоянии, в котором для каждой ее части, также являющейся самой по себе макросистемой, физические величины с большой относительной точностью равны своим средним значениям, то рассматриваемая замкнутая система находится в состоянии статистического равновесия. Если система наблюдается в течение достаточно большого промежутка времени, то подавляющую часть этого промежутка оно проводит в состоянии статистического равновесия. Если в какой-то начальный момент времени система не находилась в состоянии статистического равновесия (например, искусственно была выведена из него внешними воздействиями, а потом снова стала замкнутой), то в дальнейшем она обязательно перейдет в состояние статистического равновесия. Промежуток времени перехода в статистическое равновесие называется временем релаксации. §1.6. Фазовое пространство. Функция распределения. Рассмотрим идеальный газ (нет взаимодействия между молекулами). Полная энергия идеального газа есть сумма кинетических энергий отдельных молекул: Подсистему (молекулу) будем характеризовать координатами и скоростями (или импульсами): x, y, z, px, py, pz. Таким образом, 6 величин задают положение частицы и ее состояние.
Рис.1.1. Координатное и импульсное фазовые пространства. Введем понятие фазового пространства как пространства координат и импульсов (скоростей). Для подсистемы из одной молекулы это 6-ти мерное пространство. Различные состояния частицы можно изображать точками этого фазового пространства. С течением времени состояние частицы будет меняться, и тогда, соединяя все положения точек в различные моменты времени, получим фазовую линию в этом пространстве. Если система состоит из двух молекул, то их состояние задается 6+6 = 12 величинами, и мы имеем 12-ти мерное фазовое пространство. Рассмотрим фазовое пространство в общем случае. Пусть рассматриваемая макросистема имеет n степеней свободы, т.е. положение точек этой системы в пространстве характеризуется n координатами, которые обозначим за qi (i =1,2,3,..., n). Состояние системы тогда определяется n координатами qi и n скоростями Каждая система имеет свое фазовое пространство. Вероятность реализации различных состояний системы есть функция от координат и импульсов той системы. Координаты и импульсы в этом пространстве меняются непрерывном образом, а для непрерывных значений необходимо задавать элемент объема фазового пространства (как произведение координатной и импульсной частей объема):
Это малая область пространства, куда может попасть система (поскольку точка не имеет измерения). Для одной частицы имеем
Для n частиц
Рассмотрим вероятность попадания системы в элемент этого фазового объема для идеального газа. Вероятность нахождения частицы в объеме
Рис.1.2. Элементы объёмов в координатном и импульсном фазовом пространстве.
всем коллективом и считать, сколько частиц попало в данный элемент фазового объема. Итак, для координатной части вероятность
что вносит ограничение на элементы объема импульсов. В общем случае элемент фазового объема
где Свойства функции распределения. Рассмотрим основные свойства функции распределения. Во-первых, выполняется условие нормировки
Наконец, в-третьих, функция распределения обладает свойством стационарности. Рассматриваем подсистему в течение большого промежутка времени, который разобьем на большое число маленьких промежутков с моментами времени между ними t 1, t 2, t 3,.... В эти моменты времени подсистема в фазовом пространстве изображается точкой. Количество этих точек в единице объема этого пространства (т.е. их плотность) будет пропорционально значению функции распределения Через момент времени D t состояния всех одновременно рассматриваемых подсистем изменяется согласно уравнениям механики. Новые состояния подсистем (они совпадают с состояниями исходной подсистемы в моменты t 1+D t, t 2+D t,....) изобразятся в фазовом пространстве точками, которые с тем же правом, что и предыдущие, будут распределены с плотностью ~ Теорема Лиувилля. Всякий объем фазового пространства при своем движении соответствующего изменению состояния системы остается по величине неизменным. Другими словами, если в начальный момент времени фазовые точки qi, pi непрерывно заполняли некоторую область G в фазовом пространстве, а с течением времени перешли в другую область G t этого пространства, то, согласно теореме Лиувилля, соответствующие фазовые объемы равны между собой. Таким образом, движение точек, изображающих состояния системы в фазовом пространстве, подобно движению несжимаемой жидкости. Это означает, что плотности точек в этих объемах одинаковы и пропорциональны
Для того, чтобы функция распределения Таким образом, для идеального газа и вообще для любой квазизамкнутой системы функция распределения §1.7. Функция распределения по энергиям. Учитывая определяющую роль энергии, естественно перейти от вероятности попадания молекулы в объем Вероятность того, что энергия молекулы находится в диапазоне (E ¸ E + dE), равна по теореме о сложении вероятностей
где интегрирование ведется по шаровому слою от p до p + dp. Так как шаровой слой очень тонкий, то
Здесь введено обозначение Объем шарового слоя равен
Функция распределения молекул по их энергиям, следовательно, определяется соотношением Важно отличать друг от друга две функции распределения. Функция микрораспределения Функция макрораспределения Зависимость
Выражение (1.43) выполняется только тогда, когда
где a и b неизвестные пока постоянные. Итак, в общем случае
До сих пор рассматривали идеальный газ. Однако все эти рассуждения могут быть применены к произвольному макроскопическому телу (неидеальные газы, жидкость, твердое тело). Для этого надо выразить дифференциал d G E через дифференциал dE и ввести функцию макрораспределения подсистемы по энергиям:
§1.8. Энтропия. Флуктуации аддитивных величин. Итак, нам известно, что статистическое поведение и свойства замкнутой (квазизамкнутой) системы определяются аддитивными интегралами движения. Одним из наиболее важных свойств аддитивных величин является то, что их флуктуации в состоянии равновесия малы (
При выводе этой формулы мы воспользовались тем, что
Тогда для относительной квадратичной флуктуации получаем:
Как видно из этого соотношения, при больших значениях N относительные флуктуации ничтожно малы. Как и для распределения молекул по объему квазизамкнутая система живет подавляющую часть времени в состоянии с энергией близкой к средней энергии. Иначе, энергия равновесной подсистемы E практически постоянна во времени и равна своему среднему значению:
где Статистический вес. По порядку величины
Здесь Введем понятие статистического веса как числа микросостояний реализующих данное макросостояние. При статистическом описании тепловых свойств тел роль статистического веса играет фазовый объем
где Если подсистему со средней энергией
Энтропия. Удобнее вводить аддитивную величину, характеризующую макроскопическое состояние подсистемы (аддитивные величины обладают малыми флуктуациями). Энтропия подсистемы определяется соотношением
Энтропия дает информацию, как и статистический вес, о полном числе микросостояний подсистемы, которые реализуют данное равновесное состояние системы с энергией Из (1.51) получаем
Энтропия большой подсистемы, статистический вес которой равен произведению статистических весов малых подсистем
равна сумме энтропий её малых равновесных частей
Энтропия - аддитивная величина. Следовательно, для энтропии флуктуации также малы
Здесь первое слагаемое - приращение энтропии за счет изменения энергии тела, второе - за счет изменения объема тела.Во всех имеющихся в природе замкнутых системах энтропия никогда самопроизвольно не убывает, она увеличивается или остается постоянной ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» им. В.И.Ульянова (Ленина) С.М.Дунаевский ЛЕКЦИИ ПО КВАНТОВОЙ МЕХАНИКЕ И СТАТИСТИЧЕСКОЙ ФИЗИКЕ СТАТИСТИЧЕСКАЯ ФИЗИКА
Учебное пособие
Санкт-Петербург
Печатается по решению издательского совета факультета электроники.
С.М.Дунаевский Лекции квантовой механике и статистической физике. Статистическая физика. Учебное пособие. Данное пособие представляет собой вторую часть расширенного конспекта лекций по курсу квантовой механики и статистической физики, который читается в весеннем семестре студентам третьего курса факультета электроники Санкт-Петербургского Государственного Электротехнического Университета (“ЛЭТИ”) им. В. И. Ульянова (Ленина). В пособии изложены основные законы и приведены выводы необходимых формул классической и квантовой статистической физики.
ОГЛАВЛЕНИЕ
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , где
, где 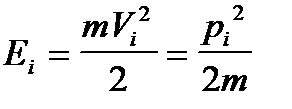 . Поскольку молекулы не взаимодействуют, то каждая молекула может быть рассмотрена как квазизамкнутая подсистема. Обмен энергиями происходит при редких столкновениях молекул. Все молекулы обладают разными скоростями, даже в положении равновесия.
. Поскольку молекулы не взаимодействуют, то каждая молекула может быть рассмотрена как квазизамкнутая подсистема. Обмен энергиями происходит при редких столкновениях молекул. Все молекулы обладают разными скоростями, даже в положении равновесия.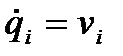 (или импульсами pi). Введем фазовое пространство системы с числом измерений 2 n. С течением времени состояние системы меняется и в фазовом пространстве, и это описывается фазовой линией.
(или импульсами pi). Введем фазовое пространство системы с числом измерений 2 n. С течением времени состояние системы меняется и в фазовом пространстве, и это описывается фазовой линией.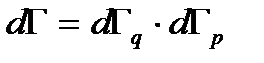 (1.33)
(1.33)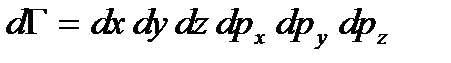 . (1.34)
. (1.34)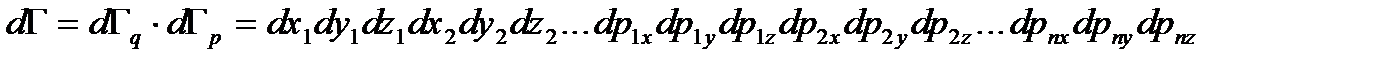 (1.35)
(1.35)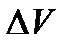 известна:
известна: 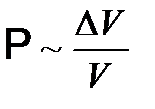 , где
, где 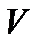 - весь пространственный объем. В силу равной вероятности нахождения частицы в любой точке пространства можно записать
- весь пространственный объем. В силу равной вероятности нахождения частицы в любой точке пространства можно записать 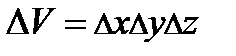 . Причем в идеальном газе можно следить за состоянием 1 частицы в течение длительного времени (и определить
. Причем в идеальном газе можно следить за состоянием 1 частицы в течение длительного времени (и определить 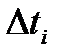 в каждом i -ом состоянии) или следить сразу за
в каждом i -ом состоянии) или следить сразу за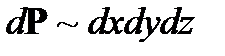 пропорциональна объёму (если нет внешнего поля). Для пространства импульсов энергия системы постоянна
пропорциональна объёму (если нет внешнего поля). Для пространства импульсов энергия системы постоянна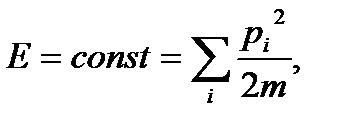 (1.36)
(1.36)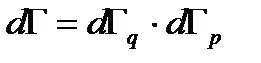 , и тогда вероятность частицы попасть в этот элемент фазового объема можно записать
, и тогда вероятность частицы попасть в этот элемент фазового объема можно записать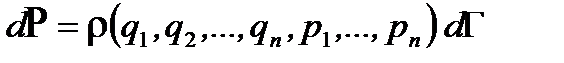 , (1.37)
, (1.37)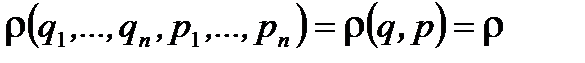 - плотность вероятности (функции распределения) для системы иметь координаты и импульсы (скорости) в этом элементе объема. Запись (1.37) для вероятности справедлива для любой квазизамкнутой системы.
- плотность вероятности (функции распределения) для системы иметь координаты и импульсы (скорости) в этом элементе объема. Запись (1.37) для вероятности справедлива для любой квазизамкнутой системы.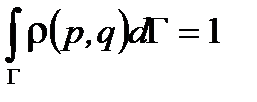 , где интегрирование ведется по всему фазовому объему. Во-вторых, среднее значение физической величины
, где интегрирование ведется по всему фазовому объему. Во-вторых, среднее значение физической величины 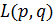 определяется выражением
определяется выражением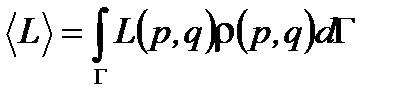 (1.38)
(1.38)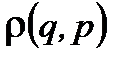 .
.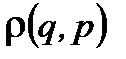 . Логично предположить, что обе совокупности точек описываются одной и той же функцией распределения. Это свойство квазизамкнутых систем называется свойством стационарности статистического распределения.
. Логично предположить, что обе совокупности точек описываются одной и той же функцией распределения. Это свойство квазизамкнутых систем называется свойством стационарности статистического распределения.  Имеет место теорема Лиувилля.
Имеет место теорема Лиувилля.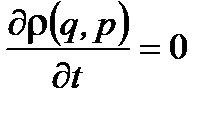 (1.39)
(1.39)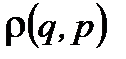 , описывающая статистическое состояние системы, зависит только от энергии. Вывод - энергия в статистике приобретает исключительную роль.
, описывающая статистическое состояние системы, зависит только от энергии. Вывод - энергия в статистике приобретает исключительную роль.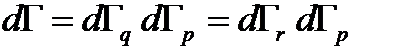 к вероятности для молекулы иметь энергию E. Для идеального газа нет необходимости рассматривать пространственную часть объема фазового пространства
к вероятности для молекулы иметь энергию E. Для идеального газа нет необходимости рассматривать пространственную часть объема фазового пространства 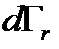 , т.к. энергия не зависит от координат для невзаимодействующих молекул. Ищем вероятность состояния молекулы с энергией в интервале от E до (E+dE),
, т.к. энергия не зависит от координат для невзаимодействующих молекул. Ищем вероятность состояния молекулы с энергией в интервале от E до (E+dE), 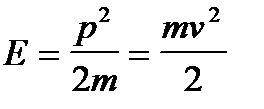 . Для определенной скорости v, или импульса p, область, соответствующая диапазону (E ¸ E + dE), имеет вид тонкого шарового слоя, радиусом
. Для определенной скорости v, или импульса p, область, соответствующая диапазону (E ¸ E + dE), имеет вид тонкого шарового слоя, радиусом 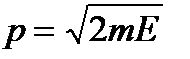
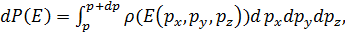 (1.40)
(1.40)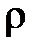 внутри можно считать постоянной. Тогда
внутри можно считать постоянной. Тогда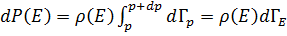 . (1.41)
. (1.41)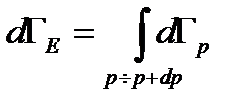 - объем шарового слоя с радиусом p. Объем шара в импульсном пространстве равен
- объем шарового слоя с радиусом p. Объем шара в импульсном пространстве равен 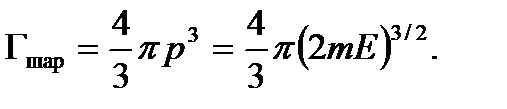
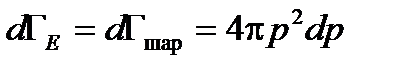 . Учитывая, что
. Учитывая, что 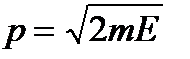 , запишем
, запишем 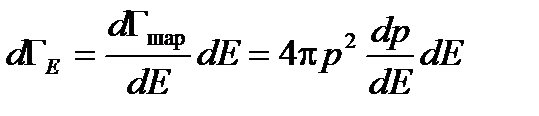 . Итак, вероятность для молекулы идеального газа иметь энергию в интервале от E до E + dE равна
. Итак, вероятность для молекулы идеального газа иметь энергию в интервале от E до E + dE равна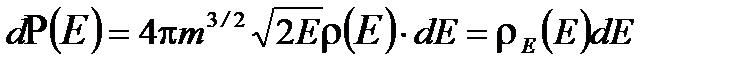 (1.42)
(1.42)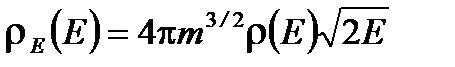 .
.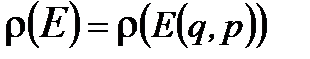 представляет собой плотность вероятности обнаружить систему в единице фазового объема с координатами q и p.
представляет собой плотность вероятности обнаружить систему в единице фазового объема с координатами q и p.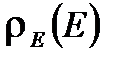
 от энергии. Используя вероятностные соображения, можно найти зависимость функции
от энергии. Используя вероятностные соображения, можно найти зависимость функции 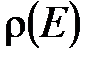 от энергии. Выделим в газе квазизамкнутую подсистему из двух невзаимодействующих молекул. Энергия подсистемы- аддитивная величина -
от энергии. Выделим в газе квазизамкнутую подсистему из двух невзаимодействующих молекул. Энергия подсистемы- аддитивная величина - 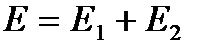 . Функция распределения подсистемы по теореме умножения вероятностей равна
. Функция распределения подсистемы по теореме умножения вероятностей равна 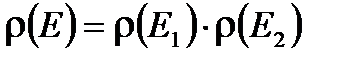 . Таким образом, функция распределения не аддитивная величина. Так как всегда удобнее работать с аддитивными величинами, то будем в квазизамкнутой системе рассматривать логарифм распределения, который есть аддитивная величина от энергии:
. Таким образом, функция распределения не аддитивная величина. Так как всегда удобнее работать с аддитивными величинами, то будем в квазизамкнутой системе рассматривать логарифм распределения, который есть аддитивная величина от энергии: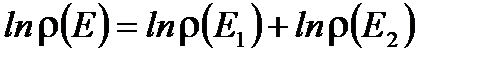 . (1.43)
. (1.43)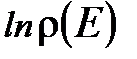 является линейной функцией энергии E
является линейной функцией энергии E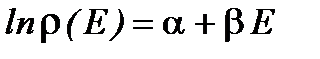 , (1.44)
, (1.44) . (1.45)
. (1.45)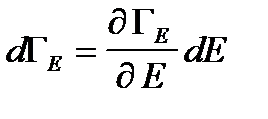 ,
, 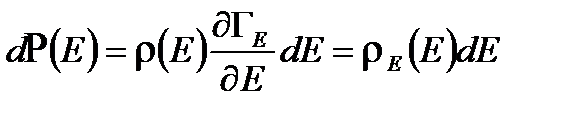 ,
, 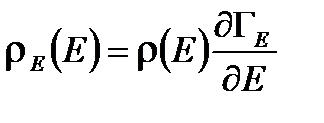 .
.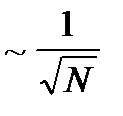 , где N число подсистем). Для доказательства разобьем квазизамкнутую подсистему на множество более мелких, квазизамкнутых одинаковых подсистем (каждая из них слабо взаимодействует с окружением). Пусть число таких подсистем N. Тогда энергия подсистемы равна сумме энергий более мелких подсистем:
, где N число подсистем). Для доказательства разобьем квазизамкнутую подсистему на множество более мелких, квазизамкнутых одинаковых подсистем (каждая из них слабо взаимодействует с окружением). Пусть число таких подсистем N. Тогда энергия подсистемы равна сумме энергий более мелких подсистем: 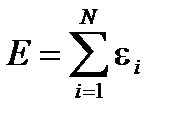 . Для оценки средней энергии подсистемы можно считать, что средние энергии малых подсистем одинаковы, поскольку мы разбивали на мелкие одинаковые подсистемы. Тогда средняя энергия равна
. Для оценки средней энергии подсистемы можно считать, что средние энергии малых подсистем одинаковы, поскольку мы разбивали на мелкие одинаковые подсистемы. Тогда средняя энергия равна  . Сосчитаем среднюю квадратичную флуктуацию
. Сосчитаем среднюю квадратичную флуктуацию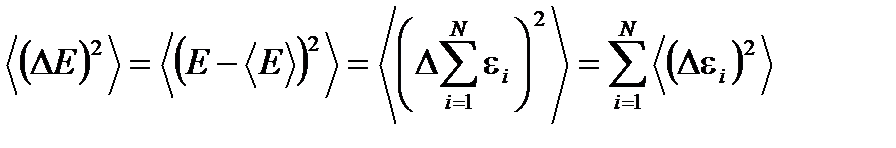 (1.46)
(1.46)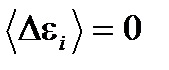 . То, что формула справедлива, проще всего увидеть на примере двух малых подсистем с энергиями e1 и e2. В самом деле, для двух подсистем
. То, что формула справедлива, проще всего увидеть на примере двух малых подсистем с энергиями e1 и e2. В самом деле, для двух подсистем 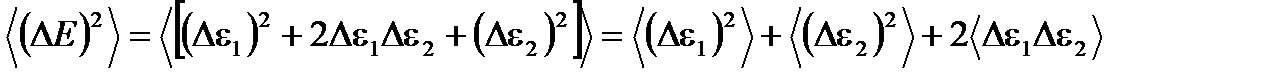 . В силу квазинезависимости малых подсистем
. В силу квазинезависимости малых подсистем 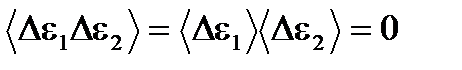 , т.к.
, т.к. 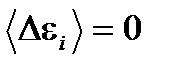 . Поэтому
. Поэтому 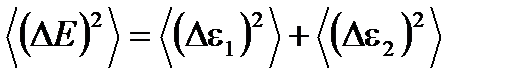 . Аналогичный результат получается и для N малых подсистем. Воспользуемся еще раз тем, что малые подсистемы примерно одинаковы, и флуктуации в них в среднем также имеют одинаковые величины
. Аналогичный результат получается и для N малых подсистем. Воспользуемся еще раз тем, что малые подсистемы примерно одинаковы, и флуктуации в них в среднем также имеют одинаковые величины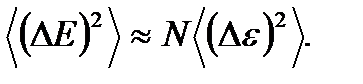 (1.47)
(1.47)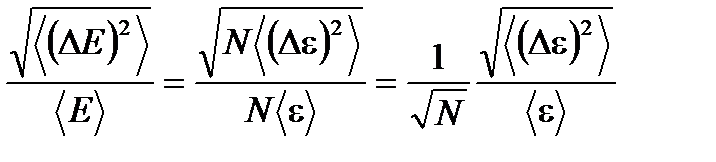 (1.48).
(1.48). . Это означает, что функция распределения имеет резкий пик при энергии
. Это означает, что функция распределения имеет резкий пик при энергии 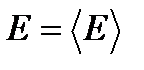 и имеет качественную зависимость, изображенную на рисунке. Заметную величину
и имеет качественную зависимость, изображенную на рисунке. Заметную величину 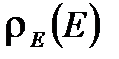 имеет только при ничтожно малых отклонениях E от среднего значения
имеет только при ничтожно малых отклонениях E от среднего значения 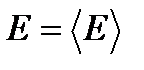 . Итак, любая квазизамкнутая система почти все время проводит в очень небольшой части фазового пространства, соответствующей энергии вблизи
. Итак, любая квазизамкнутая система почти все время проводит в очень небольшой части фазового пространства, соответствующей энергии вблизи 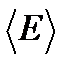 . Эту область можно оценить, исходя из того, что площадь под кривой равна единице:
. Эту область можно оценить, исходя из того, что площадь под кривой равна единице: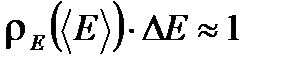 , (1.49)
, (1.49)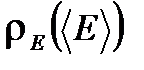 высота области, а
высота области, а 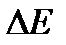 ширина этой области (на полувысоте).
ширина этой области (на полувысоте).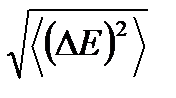 . Поэтому для оценки разрешенной части фазового пространства, в которой рассматриваемая подсистема проводит подавляющую часть времени, можно в распределении по энергиям поставить среднее значение энергии. Тогда (1.49) можно записать в виде
. Поэтому для оценки разрешенной части фазового пространства, в которой рассматриваемая подсистема проводит подавляющую часть времени, можно в распределении по энергиям поставить среднее значение энергии. Тогда (1.49) можно записать в виде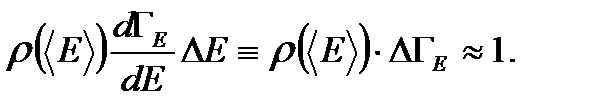 (1.50)
(1.50)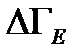 - та разрешенная часть фазового пространства, в которой рассматриваемая подсистема со средней энергией
- та разрешенная часть фазового пространства, в которой рассматриваемая подсистема со средней энергией 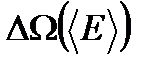 как величину, пропорциональную фазовому объему
как величину, пропорциональную фазовому объему 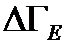 :
: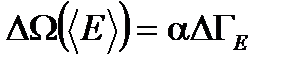 (1.51)
(1.51)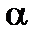 - размерный коэффициент пропорциональности.
- размерный коэффициент пропорциональности.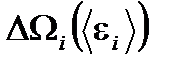 ее макросостояния с энергией в интервале от
ее макросостояния с энергией в интервале от 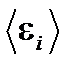 до
до 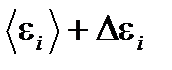 . Так как маленькие подсистемы статистически независимы, то энергия рассматриваемой подсистемы
. Так как маленькие подсистемы статистически независимы, то энергия рассматриваемой подсистемы 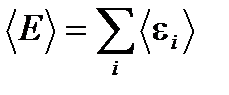 , а её статистический вес по теореме об умножении вероятностей равен
, а её статистический вес по теореме об умножении вероятностей равен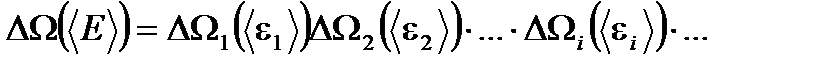 (1.52)
(1.52)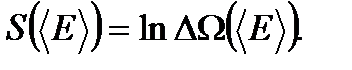 (1.53)
(1.53)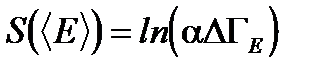 . (1.54)
. (1.54)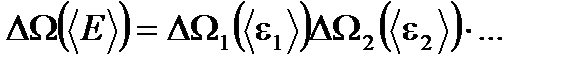 ,
,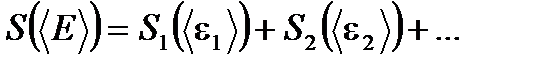 (1.55)
(1.55)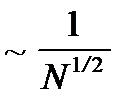 . Из свойства аддитивности следует, что энтропия помимо энергии зависит от объема тела V, но не зависит от формы тела, т.к. изменение формы тела - это только перестановка его частей, соответствующая перестановке слагаемых в сумме энтропий отдельных малых подсистем. Таким образом, энтропия
. Из свойства аддитивности следует, что энтропия помимо энергии зависит от объема тела V, но не зависит от формы тела, т.к. изменение формы тела - это только перестановка его частей, соответствующая перестановке слагаемых в сумме энтропий отдельных малых подсистем. Таким образом, энтропия 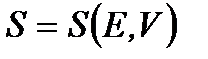 , т.е. макроскопическое состояние определяется всего двумя параметрами: энергией тела E и его объемом V. Небольшое изменение макроскопического состояния тела сопровождается малым изменением энтропии dS, которое состоит из двух вкладов
, т.е. макроскопическое состояние определяется всего двумя параметрами: энергией тела E и его объемом V. Небольшое изменение макроскопического состояния тела сопровождается малым изменением энтропии dS, которое состоит из двух вкладов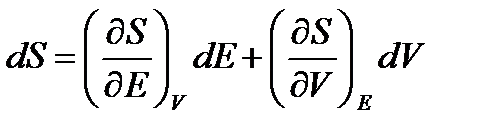 . (1.56)
. (1.56)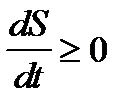 . Закон возрастания энтропии устанавливает определенное направление течения процессов в природе.
. Закон возрастания энтропии устанавливает определенное направление течения процессов в природе.


