
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Максвелла по проекциям скорости.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Когда проводится экспериментальная проверка распределения Максвелла, то регистрируются молекулы, летящие в одну сторону. Чтобы получить функцию распределения молекул по проекциям скорости перепишем распределение Максвелла в виде
Эту вероятность можно представить в виде произведения
Легко увидеть, что плотность вероятности Если рассматривать фазовый объем в распределении по проекциям скорости, то этот фазовый объем постоянен для всех значений vx, и равен dvx. Следовательно, вероятность больше там, где больше плотность частиц. Вычислим среднюю энергию, приходящуюся на одну степень свободы, т.е. сосчитаем
Так как
Итак, кинетическая энергия, приходящаяся на одну степень свободы, равна “половинке” kT, причем
§2.3. Распределение Больцмана и его свойства. В начале настоящей главы мы писали для классической подсистемы
Так как
Эта формула носит название распределения Больцмана. Если отсчет вести от точки, где
Примеры использования распределения Больцмана: 1) Распределение частиц в сосуде по высоте в однородном поле тяжести (
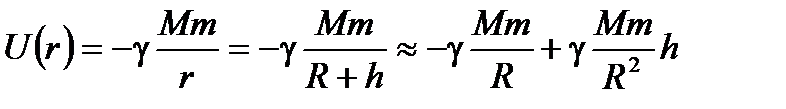 , ,
Получаем
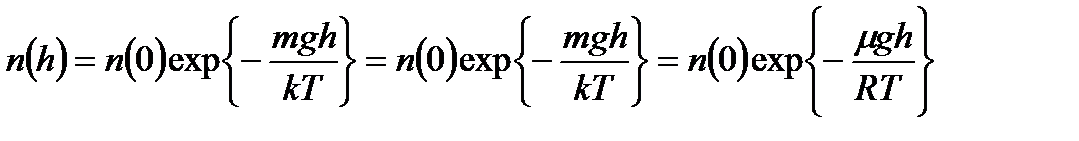 . .
Здесь m - молярная масса газа, R - универсальная газовая постоянная. Воспользовавшись связью между концентрацией и давлением, получаем барометрическую формулу Больцмана
Концентрация частиц убывает с высотой, причем концентрация более тяжелых частиц убывает с высотой быстрее. Это создает подъемную силу для более легких объектов (воздушные шары). Для более высоких температур распределение с высотой становится более равномерным. При этом полное число частиц сосуде N постоянно и равно 2) Распределение частиц во вращающемся сосуде. Имеем сосуд длины L, который вращается с угловой скоростью w вокруг одного из его оснований. Сила инерции, действующая на молекулу, находящуюся на расстоянии r от основания, равна 3) Средняя энергия, приходящаяся на колебательную степень свободы. Распределение Максвелла-Больцмана (Гиббса) позволяет получить среднюю энергию, приходящуюся на колебательную степень свободы. Этим мы подтвердим теорему о равнораспределении энергии по степеням свободы и получим теплоемкость твердых тел при высоких температурах T (для которых применимо классическое описание). Равновесное состояние кристалла - периодическое расположение атомов в пространстве. Однако, атомы не находятся в покое, а совершают малые тепловые колебания относительно положений равновесия. Пусть колебания совершаются вдоль оси 0 x, тогда энергия такого осциллятора равна:
где m масса атома,
Во избежание путаницы здесь и далее вместо kT в знаменателе стоит T. Нормировочная постоянная A состоит из произведения двух постоянных (А = А 1 А 2), которые равны соответственно:
Найдем стандартным образом среднюю энергию тела, колеблющегося вдоль оси x:
Второй интеграл в первом слагаемом есть по сути нормировочный интеграл и равен (А 2)-1. То же относится к первому интегралу во втором слагаемом, который равен (А 1)-1. Другие интегралы равны:
Подставляя (2.43) в выражение для средней энергии, получаем
Итак, на одну колебательную степень свободы приходится энергия, равная в общепринятых единицах kT. Из расчета видно, что kТ /2 возникла из-за усреднения кинетической энергии колебательного движения, а k Т /2 - из-за потенциальной энергии колебательного движения. Здесь мы доказали теорему о равномерном распределении энергии по степеням свободы. Согласно этой теореме на каждую колебательную степень свободы приходится энергия, равная kТ.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

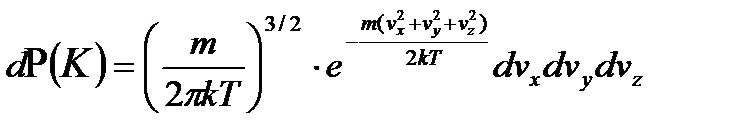 (2.32)
(2.32)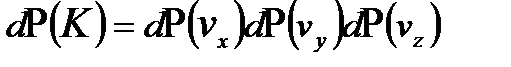 , где каждый из сомножителей представляет собой распределение Максвелла для проекций скорости молекул. Очевидно, что
, где каждый из сомножителей представляет собой распределение Максвелла для проекций скорости молекул. Очевидно, что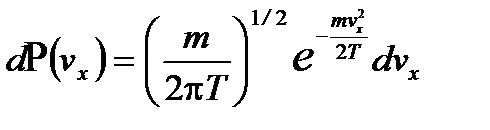 . (2.33)
. (2.33)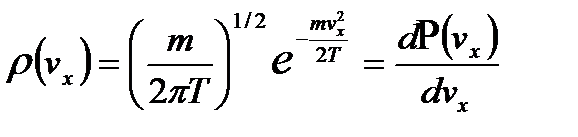 симметрично относительно начала координат и имеет максимум при vx = 0. Положительные и отрицательные значения vx имеют одинаковую вероятность, поэтому наиболее вероятная проекция и средняя проекция скорости равны нулю
симметрично относительно начала координат и имеет максимум при vx = 0. Положительные и отрицательные значения vx имеют одинаковую вероятность, поэтому наиболее вероятная проекция и средняя проекция скорости равны нулю 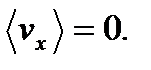 Можно пояснить на простых картинках фазового объема различие в распределениях по абсолютным значениям скорости и по их проекциям, а также, почему наиболее вероятная проекция скорости равна нулю. Плотность числа точек наибольшая в центре системы координат скоростей, а затем падает по экспоненте -
Можно пояснить на простых картинках фазового объема различие в распределениях по абсолютным значениям скорости и по их проекциям, а также, почему наиболее вероятная проекция скорости равна нулю. Плотность числа точек наибольшая в центре системы координат скоростей, а затем падает по экспоненте - 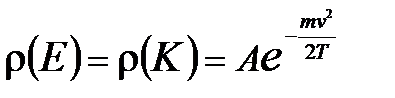 . Для абсолютных значений скорости фазовый объем растет с увеличением абсолютного значения скорости пропорционально ~ 4p v 2 dv. Поэтому при малых скоростях распределение растет из-за фазового объема, достигает максимума и затем падает из-за быстрого падения плотности частиц (хотя фазовый объем по -прежнему растет).
. Для абсолютных значений скорости фазовый объем растет с увеличением абсолютного значения скорости пропорционально ~ 4p v 2 dv. Поэтому при малых скоростях распределение растет из-за фазового объема, достигает максимума и затем падает из-за быстрого падения плотности частиц (хотя фазовый объем по -прежнему растет).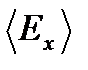 - долю кинетической энергии, относящуюся к движению по оси x. По определению
- долю кинетической энергии, относящуюся к движению по оси x. По определению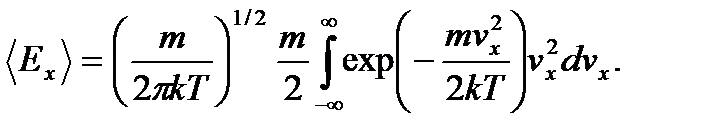
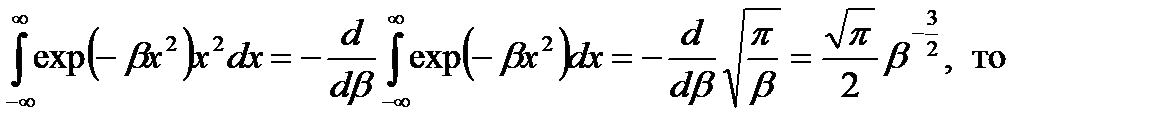
 . (2.34)
. (2.34)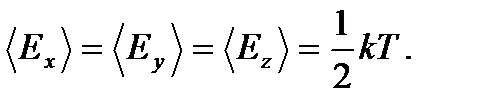 Тогда среднее значение полной энергии равно
Тогда среднее значение полной энергии равно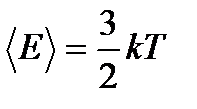 . (2.35)
. (2.35)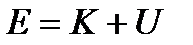 , и поскольку кинетическая энергия есть функция скоростей, а потенциальная энергия - функция координат, то вероятность для подсистемы иметь энергию Е равна
, и поскольку кинетическая энергия есть функция скоростей, а потенциальная энергия - функция координат, то вероятность для подсистемы иметь энергию Е равна 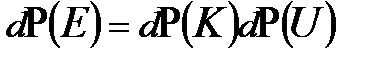 . В силу независимости событий (произведение вероятностей) иметь определенные значения кинетической и потенциальной энергий можно рассматривать отдельно вероятность распределения частиц во внешнем поле
. В силу независимости событий (произведение вероятностей) иметь определенные значения кинетической и потенциальной энергий можно рассматривать отдельно вероятность распределения частиц во внешнем поле 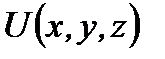
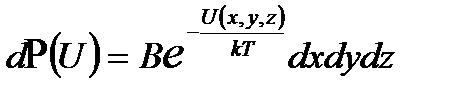 , (2.36)
, (2.36) , то число молекул в объеме
, то число молекул в объеме  определяется формулой
определяется формулой 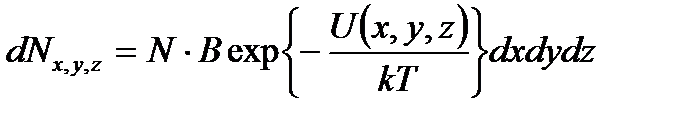 . Смысл множителя NB легко понять, если рассмотреть число частиц в единице объема, т.е. плотность (концентрацию) числа частиц
. Смысл множителя NB легко понять, если рассмотреть число частиц в единице объема, т.е. плотность (концентрацию) числа частиц 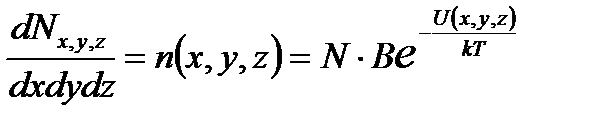 . Очевидно, что произведение NB равно плотности числа частиц
. Очевидно, что произведение NB равно плотности числа частиц 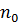 в точке, где U = 0. Тогда
в точке, где U = 0. Тогда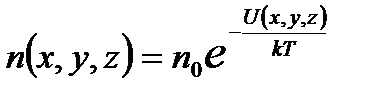 . (2.37)
. (2.37)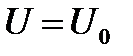 , то распределение Больцмана принимает вид
, то распределение Больцмана принимает вид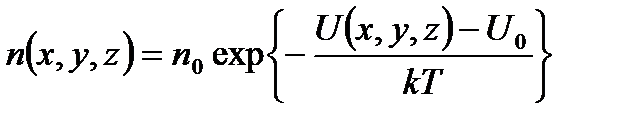 . (2.38)
. (2.38) ). Для Земли поле тяжести однородно для небольших высот h << R3 (R3 - радиус Земли):
). Для Земли поле тяжести однородно для небольших высот h << R3 (R3 - радиус Земли):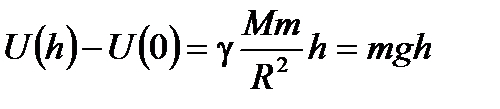 .
.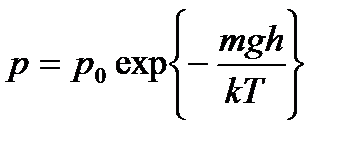 (2.39)
(2.39)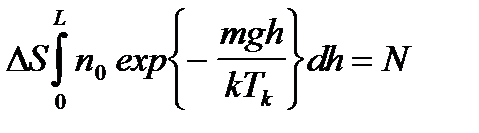 . Здесь D S площадь сечения сосуда, а L его полная высота;
. Здесь D S площадь сечения сосуда, а L его полная высота; , а потенциальная энергия молекулы равна
, а потенциальная энергия молекулы равна 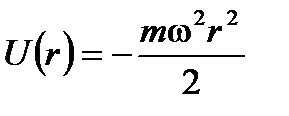 . Распределение частиц описывается функцией
. Распределение частиц описывается функцией 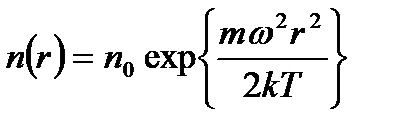 ,которая показывает, что концентрация молекул растет с радиусом и достигает максимального значения у противоположного основания;
,которая показывает, что концентрация молекул растет с радиусом и достигает максимального значения у противоположного основания;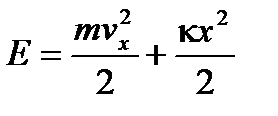 (2.40)
(2.40)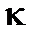 упругая постоянная. Статистическое описание атомов с энергией Е можно вести с помощью распределения Максвелла-Больцмана, которое для одного осциллятора имеет вид
упругая постоянная. Статистическое описание атомов с энергией Е можно вести с помощью распределения Максвелла-Больцмана, которое для одного осциллятора имеет вид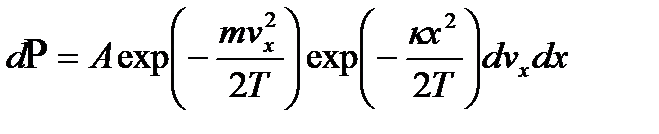 . (2.41)
. (2.41)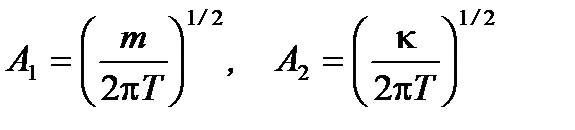 . (2.42)
. (2.42)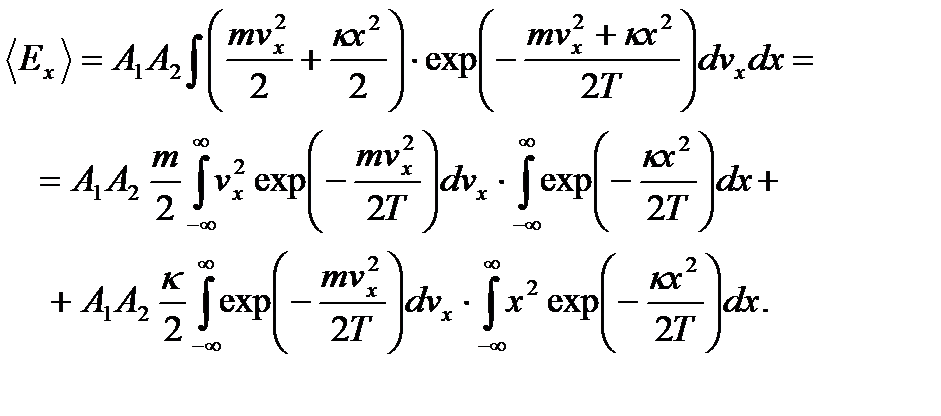
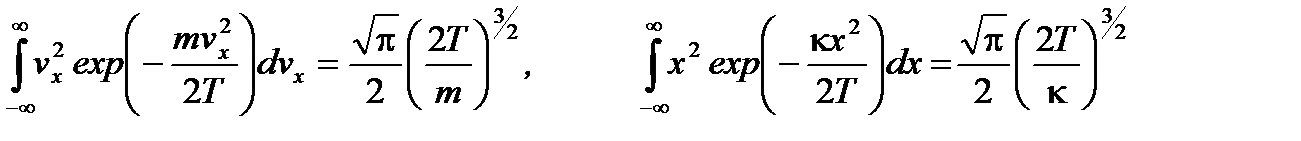 . (2.43)
. (2.43)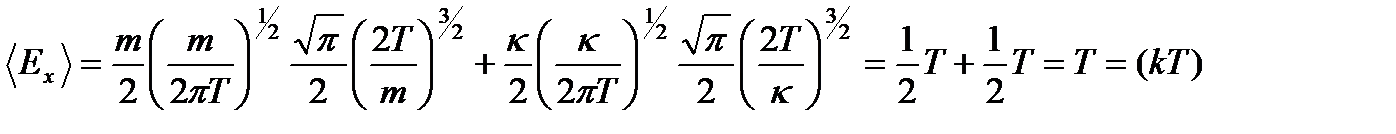 (2.44)
(2.44)


