
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ток смещения, система уравнений Максвелла.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ток смещения или абсорбционный ток — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного поля для описания слабых токов, возникающих при смещении заряженных частиц в диэлектриках. В природе существует два вида токов: ток проводимости и ток смещения. Во времена Максвелла, ток проводимости мог быть экспериментально зарегистрирован и измерен (например, амперметром, индикаторной лампой), тогда как движение зарядов внутри диэлектриков могло быть лишь косвенно оценено. При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения. Ток смещения существует и в проводниках по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:
В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому надо писать уравнение Максвелла так - Максвелла уравнения, фундаментальные уравнения классической макроскопической электродинамики, описывающие электромагнитные явления в произвольной среде. Максвелла уравнения сформулированы Дж. К. Максвеллом в 60-х годах 19 века на основе обобщения эмпирических законов электрических и магнитных явлений. Опираясь на эти законы и развивая плодотворную идею М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля, Максвелл создал теорию электромагнитных процессов, математически выражаемую Максвелла уравнения Современная форма Максвелла уравнения дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом.
Максвелла уравнения связывают величины, характеризующие электромагнитное поле, с его источниками, то есть с распределением в пространстве электрических зарядов и токов. В пустоте электромагнитное поле характеризуется двумя векторными величинами, зависящими от пространственных координат и времени: напряжённостью электрического поля Е и магнитной индукцией В. Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задаётся плотностью заряда r (зарядом в единице объёма) и плотностью тока j (зарядом, переносимым в единицу времени через единичную площадку, перпендикулярную направлению движения зарядов). Для описания электромагнитных процессов в материальной среде (в веществе), кроме векторов Е и В, вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: электрическая индукция D и напряжённость магнитного поля Н.
Максвелла уравнения позволяют определить основные характеристики поля (Е, В, D и Н) в каждой точке пространства в любой момент времени, если известны источники поля j и r как функции координат и времени. Максвелла уравнения могут быть записаны в интегральной или в дифференциальной форме (ниже они даны в абсолютной системе единиц Гаусса; см. СГС система единиц).
Максвелла уравнения в интегральной форме определяют по заданным зарядам и токам не сами векторы поля Е, В, D, Н в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов Е и Н вдоль произвольных замкнутых контуров и потоки векторов D и B через произвольные замкнутые поверхности.
Первое Максвелла уравнения является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.
Первое Максвелла уравнения имеет вид:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.100 (0.012 с.) |

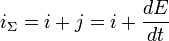 Надо для различия тока проводимости и тока смещения обозначать разными символами - i и j.
Надо для различия тока проводимости и тока смещения обозначать разными символами - i и j.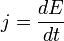 Этим восстанавливается историческая справедливость Максвелла, когда он определил, что свет есть электромагнитная волна с векторами Н и Е -
Этим восстанавливается историческая справедливость Максвелла, когда он определил, что свет есть электромагнитная волна с векторами Н и Е - 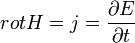
 то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S
то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S  , — проекция плотности тока смещения на ту же нормаль, а с = 3×1010 см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.
, — проекция плотности тока смещения на ту же нормаль, а с = 3×1010 см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.


