
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновое уравнение для эпизодических колебаний. Вектор пойтинга.Содержание книги
Поиск на нашем сайте
Продифференцируем дважды по каждой переменной уравнение (8.6):
Сложим последние три уравнения и получим
Из (8.7) следует
Это уравнение носит название волнового уравнения. Всякая функция, удовлетворяющая этому уравнению описывает некоторую волну. Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред.
Интерференция волн, условия максимума и минимума. Интерференция волн возможна только при выполнении условия когерентности. Слово когерентность означает согласованность. Когерентными называются колебания с одинаковой частотой и постоянной во времени разностью фаз. Интерференция волн - явление, наблюдающееся при одновременном распространении в пространстве нескольких волн и состоящее в стационарном (или медленно изменяющемся) пространственном распределении амплитуды и фазы результирующей волны. Интерференция волн - это явление усиления или ослабления колебаний, которое происходит в результате сложения двух или нескольких волн с одинаковыми периодами, распространяющихся в пространстве, и зависит от соотношения между фазами складывающихся колебаний. Явление интерференции происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях. При этом оно наблюдается и у волн, распространяющихся в средах, и у электромагнитных волн То есть интерференция является свойством волн как таковых и не зависит ни от свойств среды, ни от ее наличия. Чтобы понять ее механизм, проще всего вернуться к примеру волн на водной поверхности и представить себе, что каждая волна несет в себе инструкцию для элементов поверхности, например «подняться на 1 метр» или «опуститься на 30 см». В точке взаимодействия двух волн поверхность просуммирует две такие инструкции — в данном примере, она поднимется на 70 см (1 метр минус 30 см). Самое поразительное происходит в точке встречи двух волн равной амплитуды, достигших места встречи в противофазе (то есть когда пик максимума амплитуды одной волны накладывается на пик минимума амплитуды другой). В таком случае, условно говоря, одна волна передает поверхности инструкцию «подняться на 1 м», а другая — «опуститься на 1 м», в результате чего поверхность воды просто остается на месте. В этом случае на воде мы наблюдаем точку штиля. В акустике — мертвую точку. В оптике — точку полного затемнения. Это явление называется интерференционным гашением волн, или деструктивной интерференцией. Возможна и прямо противоположная ситуация, когда две волны встречаются в точке совпадения фаз, и амплитуды колебаний среды складываются (при равной амплитуде встретившихся волн, например, амплитуда линейных колебаний среды удвоится). Это явление называется интерференционным усилением волн, или конструктивной интерференцией. Волны на поверхности воды в таких точках будут самыми высокими, звуки — самыми громкими, свет — самым ярким. Естественно, имеется множество промежуточных значений интерференционной амплитуды колебаний, лежащих в пределах от полностью конструктивной до полностью деструктивной интерференции, которые образуют причудливую и в то же время упорядоченную интерференционную картину взаимодействия волн.
Стоячие волны. Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны
и уравнения отраженной волны Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме
Это уравнение стоячей волны определяет смещение любой точки волны.
не зависит от времени и определяет амплитуду любой точки с координатой х. Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда Аст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния х. Если придавать х значения, равные
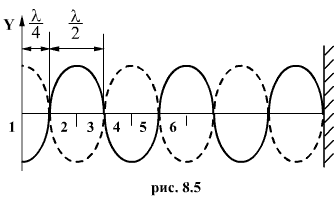
где λ - длина бегущей волны. В стоячей волне все точки среды, в которой они распространяются, расположенные между двумя соседними узлами, колеблются в одной фазе. Точки среды, лежащие по разные стороны от узла, колеблются в противофазе -фазы их отличаются на π. т.е. при переходе через узел фаза колебаний скачкообразно меняется на π. В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная волны переносят энергию в равных количествах и в прямом и в противоположном направлениях. В том случае, когда волна отражается от среды более плотной, чем та среда, где распространяется волна, в месте отражения возникает узел, фаза изменяется на противоположную. При этом говорят, что происходит потеря половины волны. Когда волна отражается от среды менее плотной в месте отражения, появляется кучность, и потери половины волны нет.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.006 с.) |

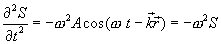

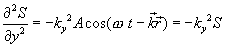

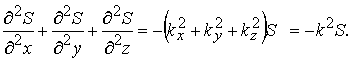
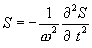
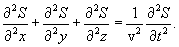
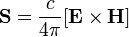
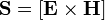 где E и H — векторы напряжённости электрического и магнитного полей соответственно.
где E и H — векторы напряжённости электрического и магнитного полей соответственно. где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.



 . После несложных преобразований, получаем
. После несложных преобразований, получаем

 и т.д., то при подстановке в уравнение (8.16) получим
и т.д., то при подстановке в уравнение (8.16) получим  . Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
. Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно



