
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия магнитного поля. Плотность энергии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Энергия магнитного поля. Плотность энергии.Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.
18. Магнитное поле в веществе, вектор намагничивания, описание поля в магнетиках. Элементарные частицы обладают внутренним квантовомеханическим свойством известным как спин. Оно аналогично угловому моменту объекта вращающегося вокруг собственного центра масс, хотя строго говоря, эти частицы являются точечными и нельзя говорить об их вращении. Спин измеряют в единицах приведённой планковской постоянной (
Магнитное поле, создаваемое магнитным моментом атома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона как и всех фермионов подчиняться правилу запрета Паули, по которому два электрона не могут находится в одном и том же квантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов. В ферромагнитных элементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседних атомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когда магнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалы состоят из атомов, магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля. Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесии спины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких как ксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемого гиперполяризацией. Это состояние имеет важное прикладное значение в магнитно-резонансной томографии. Принято различать макро- и микро-токи. Макротоки - это токи, текущие по проводникам. В любом веществе электроны движутся по круговым орбитам. Движение электронов в атоме по круговым орбитам тоже приводит к созданию магнитного поля. Токи, создаваемые в веществах движущимися электронами называют микротоками. Гипотеза Ампера: в каждом веществе за счёт движения электронов возникают микротоки.
Молекулярные токи − токи, обусловленные движением электронов в атомах, ионах, молекулах. Намагниченность — характеристика магнитного состояния макроскопического физического тела. Обозначается обычно М или J. Намагниченность равна отношению магнитного момента тела к его объёму. В случае однородно намагниченного тела намагниченность определяется как магнитный момент J единицы объёма тела: J = M/V, где М — магнитный момент тела, V — его объём. В случае неоднородно намагниченного тела намагниченность определяется для каждой точки тела (точнее, для каждого физически малого объёма dV): J = dM/dV, где dM — магнитный момент объёма dV. Единица намагниченности в Международной системе единиц — ампер на метр (1 А/м — намагниченность, при которой 1 м³ вещества обладает магнитным моментом 1 А·м²), в системе СГС — эрг/(Гс·см³); 1 эрг/(Гс·см³) = 10³ А/м. Намагниченность тел зависит от внешнего магнитного поля и температуры. У ферромагнетиков зависимость J от напряжённости внешнего поля Н выражается кривой намагничивания (см. Намагничивания кривые, Гистерезис). В изотропных веществах направление J совпадает с направлением Н, в анизотропных (см. Магнитная анизотропия) направления J и Н в общем случае различны. Вектор намагничивания — магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность достигает значительных величин в анизотропных магнетиках, и близка к нулю в изотропных магнетиках. Поэтому, в последних возможно выразить вектор намагничивания через напряжённость магнитного поля и коэффициент Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе. (Объёмная) магнитная восприимчивость равна отношению намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. Она является безразмерной величиной и измеряется в безразмерных единицах. Магнитная восприимчивость, рассчитанная на единицу массы вещества, называется удельной магнитной восприимчивостью. Аналогично определяется молярная магнитная восприимчивость. Магнитная восприимчивость может быть как положительной, так и отрицательной. Отрицательной обладают диамагнетики: они намагничиваются не по полю, а против поля. У парамагнетиков и ферромагнетиков она положительна (намагничивание по полю). Магнитная восприимчивость, как правило, зависит от температуры (исключение составляют большинство диамагнетиков и некоторые парамагнетики — щелочные и, отчасти, щёлочноземельные металлы). Магнитная восприимчивость парамагнетиков уменьшается с температурой, следуя закону Кюри — Вейса. В ферромагнитных телах магнитная восприимчивость с ростом температуры увеличивается, достигая резкого максимума вблизи точки Кюри. Магнитная восприимчивость антиферромагнетиков увеличивается с ростом температуры до точки Нееля, а затем падает по закону Кюри — Вейса.
Закон полного тока в веществе. Если вещество не заполняет всего пространства, занимаемого магнитным полем или если свойства магнетика меняются от точки к точке, то учет влияния среды представляет собой сложную задачу. В этом случае оказывается удобным ввести в рассмотрение кроме индукции магнитного поля еще одну расчетную векторную величину получившую название напряженности магнитного поля. Если магнитное поле существует в однородной среде, то напряженность не зависит от магнитных свойств среды, а зависит только от силы тока, создающего поле, формы и размеров контура этого тока и положения точки в магнитном поле. Фундаментальный закон полного тока, справедливый и для случая неоднородных сред: циркуляция вектора напряженности равна алгебраической сумме токов, охватываемых контуром интегрирования. При более точной формулировке закона полного тока учитывается, что токи могут быть распределены в пространстве с некоторой плотностью. т.е. циркуляция вектора напряженности по некоторому контуру равна сумме токов, пронизывающих произвольную поверхность, опирающуюся на этот контур. Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и магнитным полем H в веществе. Обозначается μ. У изотропных веществ μ = B / H (в Международной системе единиц СИ).Выделяют относительную и абсолютную магнитные проницаемости У анизотропных тел (кристаллов) М. п. — тензор. М. п. связана с магнитной восприимчивостью c соотношением m= 1 + 4pc (в СГС системе единиц) или m = 1 +c (в ед. СИ), m измеряется в безразмерных единицах. Для физич. вакуума c = 0 и m= 1. Магнитные материалы, магнетики — материалы, вступающие во взаимодействие с магнитным полем, выражающееся в его изменении, а также в других физических явлениях — изменение физических размеров, температуры, проводимости, возникновению электрического потенциала и т. д.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.82.168 (0.009 с.) |

 Значит, энергия магнитного поля, которое связано с контуром,
Значит, энергия магнитного поля, которое связано с контуром,  Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем
Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем  Так как I=B l /(μ0μN) и В=μ0μH, то
Так как I=B l /(μ0μN) и В=μ0μH, то  где S l = V — объем соленоида. Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью
где S l = V — объем соленоида. Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью  Формула для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н, т.е. оно относится только к пара- и диамагнетикам.
Формула для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н, т.е. оно относится только к пара- и диамагнетикам. ), тогда электроны, протоны и нейтроны имеют спин равный ½
), тогда электроны, протоны и нейтроны имеют спин равный ½  названный магнитной восприимчивостью:
названный магнитной восприимчивостью: 
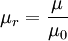 где μr - относительная, а μ - абсолютная проницаемость, μ0 — магнитная постоянная.
где μr - относительная, а μ - абсолютная проницаемость, μ0 — магнитная постоянная.


