

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Волновое уравнение для электромагнитного поля. Свойства
Похожие статьи вашей тематики
Волновое уравнение для электромагнитного поля. Покажем, что существование электромагнитных волн вытекает из уравнений Максвелла. В случае однородной нейтральной непроводящей среды с постоянными проницаемостями 
Поэтому уравнения (71.1) — (71.4) можно написать следующим образом:  (104.1) Возьмем ротор от обеих частей уравнения (104.1): (104.1) Возьмем ротор от обеих частей уравнения (104.1):  (104.5) Символ означает дифференцирование по координатам. Изменение последовательности дифференцирования по координатам и времени приводит к равенству (104.5) Символ означает дифференцирование по координатам. Изменение последовательности дифференцирования по координатам и времени приводит к равенству 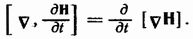 Произведя в (104.5) такую замену и подставив в получившееся уравнение значение (104.3) для ротора Н, получим Произведя в (104.5) такую замену и подставив в получившееся уравнение значение (104.3) для ротора Н, получим 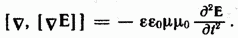 (104.6) Согласно (11.40). В силу (104.4) первый член этого выражения равен нулю. Поэтому левая часть формулы (104.6) представляет собой. Таким образом, опустив слева и справа знак минус, приходим к уравнению (104.6) Согласно (11.40). В силу (104.4) первый член этого выражения равен нулю. Поэтому левая часть формулы (104.6) представляет собой. Таким образом, опустив слева и справа знак минус, приходим к уравнению  В соответствии с (39.15). Поэтому уравнению можно придать вид В соответствии с (39.15). Поэтому уравнению можно придать вид  (104.7) Раскрыв оператор Лапласа, получим (104.7) Раскрыв оператор Лапласа, получим  Взяв ротор от обеих частей уравнения (104.3) и произведя аналогичные преобразования, придем к уравнению Взяв ротор от обеих частей уравнения (104.3) и произведя аналогичные преобразования, придем к уравнению  Уравнения (104.8) и (104.9) неразрывно связаны друг с другом, так как они получены из уравнений (104.1) и (104.3), каждое из которых содержит и Е, и Н.Уравнения (104.8) и (104.9) прёдставляют собой типичные волновые уравнения (см. (96.2)). Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (104.8) и (104.9) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна Уравнения (104.8) и (104.9) неразрывно связаны друг с другом, так как они получены из уравнений (104.1) и (104.3), каждое из которых содержит и Е, и Н.Уравнения (104.8) и (104.9) прёдставляют собой типичные волновые уравнения (см. (96.2)). Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (104.8) и (104.9) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна  (104.10) В вакууме (т. е. при) скорость электромагнитных волн совпадает со скоростью света в пустоте с. (104.10) В вакууме (т. е. при) скорость электромагнитных волн совпадает со скоростью света в пустоте с.
| Свойства электромагнитных волн. Электромагнитные волны представляют собой распространение электромагнитных полей в пространстве и времени.Рассмотрим основные свойства электромагнитных волн. 1. Электромагнитные волны излучаются колеблющимися зарядами. Наличие ускорения - главное условие излучения электромагнитных волн. 2. Такие волны могут распространяться не только в газах, жидкостях и твердых средах, но и в вакууме. 3. Электромагнитная волна является поперечной.. Периодические изменения электрического поля (вектора напряженности Е) порождают изменяющееся магнитное поле (вектор индукцииВ), которое в свою очередь порождает изменяющееся электрическое поле. Колебания векторов Е и В происходят во взаимно перпендикулярных плоскостях и перпендикулярно линии распространения волны (вектору скорости) и в любой точке совпадают по фазе. Силовые лини электрического и магнитного полей в электромагнитной волне являются замкнутыми. Такие поля называют вихревыми.
| 4. Скорость электромагнитных волн в вакууме с=300000 км/с. Распространение электромагнитной волны в диэлектрике представляет собой непрерывное поглощение и переизлучение электромагнитной энергии электронами и ионами вещества, совершающими вынужденные колебания в переменном электрическом поле волны. При этом в диэлектрике происходит уменьшение скорости волны.
5. При переходе из одной среды в другую частота волны не изменяется. 6. Электромагнитные волны могут поглощаться веществом. Это обусловлено резонансным поглощением энергии заряженными частицами вещества. Если собственная частота колебаний частиц диэлектрика сильно отличается от частоты электромагнитной волны, поглощение происходит слабо, и среда становится прозрачной для электромагнитной волны. 7. Попадая на границу раздела двух сред, часть волны отражается, а часть проходит в другую среду, преломляясь. Если второй средой является металл, то прошедшая во вторую среду волна быстро затухает, а большая часть энергии (особенно у низкочастотных колебаний) отражается в первую среду (металлы являются непрозрачными для электромагнитных волн)
67. Энергия электромагнитных волн. Вектор Пойнтинга.
Энергия электромагнитных волн. Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях. В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна  (1.1) а магнитного поля – (1.1) а магнитного поля –  (1.2) где (1.2) где  и и  – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна  (1.3) Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением (1.3) Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением  , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля: , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:  (1.4) Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Плотность энергии электромагнитного поля можно представить в виде: (1.4) Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Плотность энергии электромагнитного поля можно представить в виде:  (1.5). Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства. Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия (1.5). Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства. Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия  , равная , равная  , где , где  – скорость электромагнитной волны в вакууме. Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны: – скорость электромагнитной волны в вакууме. Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:  (1.6) Подставляя в последнее соотношение выражения для (1.6) Подставляя в последнее соотношение выражения для  и и  , получим , получим  . .
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:  (в системе СГС), (в системе СГС),  (в системе СИ), где E и H — векторы напряжённости электрического и магнитного полей соответственно. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии: (в системе СИ), где E и H — векторы напряжённости электрического и магнитного полей соответственно. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии:  (в системе СГС), (в системе СГС),  (в системе СИ), где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи. Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред. (в системе СИ), где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи. Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.
Излучение диполя.
ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ - излучение, обусловленное изменением во времени дипольного момента системы. В случав эл--магн. Д. и., о к-ром далее только и будет идти речь, различают электрич. и магн. Д. и. в зависимости от того, вызывается ли оно изменением электрич. ре или магн. рm дипольных моментов.
Классическая теория. Произвольное распределение неподвижных или движущихся зарядов можно описать с помощью плотностей заряда  и тока j, удовлетворяющих ур-нию непрерывности: и тока j, удовлетворяющих ур-нию непрерывности:  . Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения . Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения  ; ;  . Это ограничивает скорости и движения зарядов нерелятивистскими значениями, . Это ограничивает скорости и движения зарядов нерелятивистскими значениями,  . Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам . Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам   , и магнитного, соответствующего токам , и магнитного, соответствующего токам   . Здесь . Здесь  - дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников, - дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников,  , т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:) , т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:)  Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа( Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа(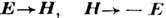 , ,  ). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ. ). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ.
В случае гармонич. закона изменения дипольного момента,  , с частотой , с частотой  ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна  , а её угл. распределение (диаграмма направленности) имеет вид: , а её угл. распределение (диаграмма направленности) имеет вид:  где где  - интенсивность, отнесённая к единице телесного угла, - интенсивность, отнесённая к единице телесного угла,  - угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l: - угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l:  (элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S: (элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S:  и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то   . При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение). . При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение).
|




 (104.1) Возьмем ротор от обеих частей уравнения (104.1):
(104.1) Возьмем ротор от обеих частей уравнения (104.1):  (104.5) Символ означает дифференцирование по координатам. Изменение последовательности дифференцирования по координатам и времени приводит к равенству
(104.5) Символ означает дифференцирование по координатам. Изменение последовательности дифференцирования по координатам и времени приводит к равенству 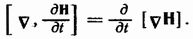 Произведя в (104.5) такую замену и подставив в получившееся уравнение значение (104.3) для ротора Н, получим
Произведя в (104.5) такую замену и подставив в получившееся уравнение значение (104.3) для ротора Н, получим 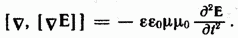 (104.6) Согласно (11.40). В силу (104.4) первый член этого выражения равен нулю. Поэтому левая часть формулы (104.6) представляет собой. Таким образом, опустив слева и справа знак минус, приходим к уравнению
(104.6) Согласно (11.40). В силу (104.4) первый член этого выражения равен нулю. Поэтому левая часть формулы (104.6) представляет собой. Таким образом, опустив слева и справа знак минус, приходим к уравнению  В соответствии с (39.15). Поэтому уравнению можно придать вид
В соответствии с (39.15). Поэтому уравнению можно придать вид  (104.7) Раскрыв оператор Лапласа, получим
(104.7) Раскрыв оператор Лапласа, получим  Взяв ротор от обеих частей уравнения (104.3) и произведя аналогичные преобразования, придем к уравнению
Взяв ротор от обеих частей уравнения (104.3) и произведя аналогичные преобразования, придем к уравнению  Уравнения (104.8) и (104.9) неразрывно связаны друг с другом, так как они получены из уравнений (104.1) и (104.3), каждое из которых содержит и Е, и Н.Уравнения (104.8) и (104.9) прёдставляют собой типичные волновые уравнения (см. (96.2)). Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (104.8) и (104.9) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна
Уравнения (104.8) и (104.9) неразрывно связаны друг с другом, так как они получены из уравнений (104.1) и (104.3), каждое из которых содержит и Е, и Н.Уравнения (104.8) и (104.9) прёдставляют собой типичные волновые уравнения (см. (96.2)). Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (104.8) и (104.9) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна  (104.10) В вакууме (т. е. при) скорость электромагнитных волн совпадает со скоростью света в пустоте с.
(104.10) В вакууме (т. е. при) скорость электромагнитных волн совпадает со скоростью света в пустоте с. (1.1) а магнитного поля –
(1.1) а магнитного поля –  (1.2) где
(1.2) где  и
и  – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна
– электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна  (1.3) Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением
(1.3) Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением  , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:
, то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:  (1.4) Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Плотность энергии электромагнитного поля можно представить в виде:
(1.4) Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Плотность энергии электромагнитного поля можно представить в виде:  (1.5). Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства. Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия
(1.5). Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства. Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия  , равная
, равная  , где
, где  – скорость электромагнитной волны в вакууме. Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:
– скорость электромагнитной волны в вакууме. Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:  (1.6) Подставляя в последнее соотношение выражения для
(1.6) Подставляя в последнее соотношение выражения для  и
и  .
. (в системе СГС),
(в системе СГС),  (в системе СИ), где E и H — векторы напряжённости электрического и магнитного полей соответственно. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии:
(в системе СИ), где E и H — векторы напряжённости электрического и магнитного полей соответственно. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии:  (в системе СГС),
(в системе СГС),  (в системе СИ), где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи. Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.
(в системе СИ), где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи. Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред. и тока j, удовлетворяющих ур-нию непрерывности:
и тока j, удовлетворяющих ур-нию непрерывности:  . Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения
. Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения  ;
;  . Это ограничивает скорости и движения зарядов нерелятивистскими значениями,
. Это ограничивает скорости и движения зарядов нерелятивистскими значениями,  . Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам
. Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам 
 , и магнитного, соответствующего токам
, и магнитного, соответствующего токам 
 . Здесь
. Здесь  - дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников,
- дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников,  , т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:)
, т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:)  Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа(
Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа(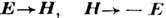 ,
,  ). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ.
). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ. , с частотой
, с частотой  ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна
ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна  , а её угл. распределение (диаграмма направленности) имеет вид:
, а её угл. распределение (диаграмма направленности) имеет вид:  где
где  - интенсивность, отнесённая к единице телесного угла,
- интенсивность, отнесённая к единице телесного угла,  - угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l:
- угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l:  (элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S:
(элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S:  и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то
и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то 
 . При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение).
. При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение).


