
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловая скорость и угловое ускорение. Связь между угловыми и линейными характеристикамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Угловая скорость и угловое ускорение. Связь между угловыми и линейными характеристиками Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени: омега=dфи/dt. Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки.При вращении точки вокруг неподвижной оси, угловое ускорение по модулю равно a=domega/dt. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости omega по времени.
Основная задача динамики Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.1)Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.2)Обратная задача динамики: по заданным силам определить характер движения тела Масса, импульс, сила. Силы в механике. Ма́сса — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: p=mV. Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений.2 з.Н.: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодейст вующей всех приложенных к ней сил и обратно пропорцио нально её массе. a=F/m. В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. F=dp/dt. 3й з Н.: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F12=-F21. Силы инерции существенно отличаются от тех сил, что фигурируют в формулировках второго и третьего законов Ньютона. В частности, они не имеют материального источника, не являются результатом взаимо действия каких-либо тел и не подчиняются третьему закону Ньютона. В связи с этим о данных силах говорят, что они не являются физическими силами, их называют фиктивными, кажущимися или псевдо силами. Cила трения- сила которая препятствует скольжению соприкасающихся тел друг относительно друга. F= fN, gde f-koofecient treniya, a N- davlenie Законы Ньютона. 1з.Н.: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. 2 з.Н.: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. a=F/m. В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. F=dp/dt. 3й з Н.: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F12=-F21.
Момент силы и момент импульса тела. Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. М= [r x F] Характеризует вращательное действие силы на твёрдое тело. Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. L=[r x p]
7) Уравнение динамики вращательного движения твердого тела. Момент инерции тела. Теорема Штейнера. Уравнение движения материальной точки: F=dp/dt. – скорость изменения импульса мат. Точки равна действу ющей на нее силе. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).Единица измерения СИ: кг·м². Теорема Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относи тельно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: J=Jc+mdd
Законы сохранения импульса и момента импульса - фундаментальные законы природы. Применение этих законов к решению задач механики. Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота. Согласно теореме Нётер каждому закону сохранения ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен Кинетическая энергия и работа при вращательном движении. Кинетическая энергия- функция состояния, или мера работоспособности движущегося тела. Сила, действуя на покоющееся тело и вызывая его движение совершает работу, а энергию движущегося тела возрастает на вел-ну затраченной работы. dA=dT. К.Э. вращ. Движения Твр= I *omega^2/2 Работа и мощность тока. Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась. Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:
По закону сохранения энергии: работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия В системе СИ:
МОЩНОСТЬ ПОСТОЯННОГО ТОКА - отношение работы тока за время t к этому интервалу времени.
В системе СИ:
Согласно Максвеллу, всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле. Циркуляция вектора напряженности E этого поля по любому неподвижному замкнутому контуру s определяется выражением
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индукцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Излучение диполя. ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ - излучение, обусловленное изменением во времени дипольного момента системы. В случав эл--магн. Д. и., о к-ром далее только и будет идти речь, различают электрич. и магн. Д. и. в зависимости от того, вызывается ли оно изменением электрич. ре или магн. рm дипольных моментов. Классическая теория. Произвольное распределение неподвижных или движущихся зарядов можно описать с помощью плотностей заряда В случае гармонич. закона изменения дипольного момента, Гипотеза Планка о квантовом характере излучения. Формула Планка. Формула Планка — выражение для спектральной плотности мощности (Спектральной Плотности Энергетической Светимости) излучения абсолютно чёрного тела, которое было получено Максом Планком. Для плотности энергии излучения Формула Планка («форма» зависимости
Коэффициент пропорциональности Гипотеза Планка. Стремясь преодолеть затруднения классической теории при объяснении излучения нагретого твердого тела, немецкий физик Макс Планк в 1900 г. высказал гипотезу, которая положила начало подлинной революции в теоретической физике. Смысл этой гипотезы заключается в том, что запас энергии колебательной системы, находящейся в равновесии с электромагнитным излучением, не может принимать любые значения. Энергия элементарных систем, поглощающих и излучающих электромагнитные волны, обязательно должна быть равна целому кратному некоторого определенного количества энергии. Минимальное количество энергии, которое система может поглотить или излучить, называется квантом энергии. Энергия кванта
Коэффициент пропорциональности Принцип соответствия Бора. Более совершенную квантовую модель атома предложил в 1913 г. молодой датский физик Н. Бор, работавший в лаборатории Резерфорда. Бор понял, что для построения теории, которая объясняла бы и результаты опытов по рассеянию α -частиц, и устойчивость атома, и сериальные закономерности, и ряд других экспериментальных данных, нужно отказаться от ряда принципов классической физики. Бор взял за основу модель атома Резерфорда и дополнил ее новыми гипотезами, которые не следуют или даже противоречат классическим представлениям. Эти гипотезы известны как постулаты Бора. Они сводятся к следующему. 2. Электрон способен переходить с одной стационарной орбиты на другую. Только в этом случае он испускает или поглощает определенную порцию энергии монохроматического излучения определенной частоты. Эта частота зависит от уровня изменения энергии атома при таком переходе. Бор предложил грубый критерий для классического предела: переход происходит, когда квантовые числа, описывающие систему являются большими, означая или возбуждение системы до больших квантовых чисел, или то, что система описана большим набором квантовых чисел, или оба случая. Более современная формулировка говорит, что классическое приближение справедливо при больших значениях действия
(произведение характерного импульса процесса на его характерный размер и произведение характерной энергии процесса на его характерное время значительно больше Принцип соответствия — один из инструментов, доступных физикам для того, чтобы выбрать соответствующую действительности квантовую теорию. Принципы квантовой механики довольно широки — например, они заявляют, что состояния физической системы занимают Гильбертово пространство, но не говорят, какое именно. Принцип соответствия ограничивает выбор теми пространствами, которые воспроизводят классическую механику в классическом пределе. Угловая скорость и угловое ускорение. Связь между угловыми и линейными характеристиками Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени: омега=dфи/dt. Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки.При вращении точки вокруг неподвижной оси, угловое ускорение по модулю равно a=domega/dt. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости omega по времени.
Основная задача динамики Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.1)Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.2)Обратная задача динамики: по заданным силам определить характер движения тела
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.236.188 (0.014 с.) |





 , где Ф – магнитный поток, пронизывающий контур s.
, где Ф – магнитный поток, пронизывающий контур s. и тока j, удовлетворяющих ур-нию непрерывности:
и тока j, удовлетворяющих ур-нию непрерывности:  . Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения
. Поле, создаваемое такими источниками вне области их размещения, описывается как совокупность полей мультиполей: монополя (заряда), диполя, квадруполя и т. д. Однако такое описание продуктивно только тогда, когда размер l области, содержащей источники, мал по сравнению с длиной волны излучения  ;
;  . Это ограничивает скорости и движения зарядов нерелятивистскими значениями,
. Это ограничивает скорости и движения зарядов нерелятивистскими значениями,  . Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам
. Д.и. из таких областей можно представить как излучение сосредоточенного (точечного) дипольного момента - электрического, соответствующего источникам 
 , и магнитного, соответствующего токам
, и магнитного, соответствующего токам 
 . Здесь
. Здесь  - дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников,
- дельта-функция Дирака, а точка - знак дифференцирования по времени. Поле излучения создаётся только соленоидальными частями этих распределений, потенц. части ответственны лишь за квазистатич. поля. На больших расстояниях R от области источников,  , т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:)
, т. е. в волновой зоне (см. Антенна),электрическое E и магнитное H поля в вакуумевыражают след. ф-лами (Гаусса система единиц:)  Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа(
Здесь n - единичный вектор вдоль R, запаздывающий аргумент t-R/c учитывает разницу между моментом возникновения волнового возмущения в точке источника и моментом прихода его в точку наблюдения. Поле магн. Д. и. получают отсюда при помощи двойственности перестановочной принципа(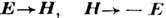 ,
,  ). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ.
). Эл--магн. поле (*) представляет собой сферически расходящуюся волну с векторами E и H, перпендикулярными направлению её распространения, т. е. вдали от источников это квазиплоские волны типа ТЕМ. , с частотой
, с частотой  ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна
ср. интенсивность излучения в единицу времени (ср. мощность излучения) равна  , а её угл. распределение (диаграмма направленности) имеет вид:
, а её угл. распределение (диаграмма направленности) имеет вид:  где
где  - интенсивность, отнесённая к единице телесного угла,
- интенсивность, отнесённая к единице телесного угла,  - угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l:
- угол между п и р0. Обычно (но не всегда!) магн. Д. и. меньше электрич. Д. и. и сопоставимо лишь с электрич. квадрупольным излучением. Если диполь электрический представить как элемент тока J длины l:  (элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S:
(элементарный вибратор, или диполь Герца), а диполь магнитный - как рамку с током J и площадью S:  и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то
и считать токи одинаковыми, а размеры области источников соизмеримыми (S~ l 2), то 
 . При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение).
. При движении гармонически колеблющегося диполя в пространстве частота его Д. и. зависит от направления излучения (см. Доплера эффект), а диаграмма направленности искажается, стягиваясь к направлению движения диполя (см. также Синхротронное излучение, Ондуляторное излучение). :
: 
 от частоты и температуры) первоначально была «выведена» эмпирически. Формула Планка была получена после того, как стало ясно, что формула Рэлея—Джинса, которая следует из классической теории электромагнитного поля, удовлетворительно описывает излучение только в области длинных волн. С убыванием длин волн формула Рэлея—Джинса сильно расходится с эмпирическими данными. Более того, в пределе она даёт расхождение — бесконечную энергию излучения (ультрафиолетовая катастрофа). В связи с этим Планк в 1900 году сделал предположение, противоречащее классической физике, о том, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:
от частоты и температуры) первоначально была «выведена» эмпирически. Формула Планка была получена после того, как стало ясно, что формула Рэлея—Джинса, которая следует из классической теории электромагнитного поля, удовлетворительно описывает излучение только в области длинных волн. С убыванием длин волн формула Рэлея—Джинса сильно расходится с эмпирическими данными. Более того, в пределе она даёт расхождение — бесконечную энергию излучения (ультрафиолетовая катастрофа). В связи с этим Планк в 1900 году сделал предположение, противоречащее классической физике, о том, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:
 впоследствии назвали постоянной Планка,
впоследствии назвали постоянной Планка,  должна быть пропорциональна частоте колебаний
должна быть пропорциональна частоте колебаний  :
: . (82.1)
. (82.1) в этом выражении носит название постоянной Планка. Постоянная Планка равна 6,626·10-34 Дж·с.
в этом выражении носит название постоянной Планка. Постоянная Планка равна 6,626·10-34 Дж·с. . В терминах «школьной» физики это означает, что должны соблюдаться неравенства:
. В терминах «школьной» физики это означает, что должны соблюдаться неравенства:




