
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критические скорости вращения роторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При определенных скоростях вращения роторов возникают поперечные изгибные колебания, которые в некоторых случаях служат причиной разрушения конструкции. Причинами, вызывающими колебания, могут быть: неуравновешенность деталей ротора, биение опор, неоднородность воздействия газового потока на лопатки, несоосности валов и соединительных муфт и т. д. При вращении роторов ГТД из-за неуравновешенности масс (дисбаланс), зазоров в опорах достичь математически точного совпадения центра тяжести ротора с геометрической осью вала практически нереально. Из-за эксцентричного положения центра масс относительно оси вала возникает неуравновешенная центробежная сила, возрастающая с дисбалансом и числом оборотов ротора, приводящая к прогибу вала. Изгибная податливость ротора в целом невелика, однако при некоторых угловых скоростях вращения ротора вал теряет устойчивость, прогибы и динамические напряжения интенсивно растут. При этом возможно задевание лопаток за корпус, разрушение подшипников и лабиринтных уплотнений, рост вибрации всей силовой установки и даже разрушение ротора. 3.1. РАСЧЕТ КРИТИЧЕСКОЙ СКОРОСТИ ВРАЩЕНИЯ НЕВЕСОМОГО ВАЛА С ДИСКОМ
Рассмотрим расчётную схему равномерно вращающегося с угловой скоростью
Рис.3.1. Расчетная схема ротора с одним диском
При вращении ротора из-за эксцентриситета возникает центробежная сила Центробежная сила определится:
При прогибе вала из-за его жёсткости возникает сила упругого противодействия
где с - коэффициент жесткости - сила, вызывающая единичный прогиб. Значение коэффициента жесткости зависит от расстояния между опорами, расположением дисков по валу их числа и массы, заделкой опор, конструкции материала и геометрических размеров вала. Пренебрегая силами демпфирования можно записать:
выразим из формулы (3.3)
С увеличением угловой скорости
вал, теряет устойчивость, при этом прогиб вала неограниченно возрастает ( Угловая скорость вращения ротора, при которой ротор теряет устойчивость, называется критической скоростью и определяется из равенства (3.5)
В реальном роторе из-за сил демпфирования, трения в опорах, внутренних сил и др. прогиб является конечной величиной и поломка вала происходит не сразу, поэтому возможно дальнейшее увеличение угловой скорости
правая часть уравнения (3.7) положительна при Графическая зависимость (3.7) представлена на рис.3.2.
Рис. 3.2. Изменение прогиба вала от скорости вращения С увеличением угловой скорости При повышении Таким образом, на больших скоростях вращения происходит снижение величины прогиба у, то естьсамоцентровка ротора, при этом центр тяжести диска располагается на оси вращения (точки Ротор, вращающийся с угловой скоростью меньше критической, называется жёстким, а ротор, вращающийся с угловыми скоростями Устойчиво работают как жёсткие, так и гибкие роторы. В процессе разгона гибкие ротора проходят через критические обороты, поэтому этот переход необходимо проходить быстрее, чтобы исключить большие прогибы ротора. В реальных конструкциях рабочие обороты рассчитывают на значительном удалении от критических Критическая скорость вращения ротора численно совпадает с частотой собственных колебаний. Рассмотрим полностью уравновешенный ротор (е =0). Если такой ротор привести в колебательное движение, отклонив импульсом силы на прогиб у, то он будет совершать колебательное движение по уравнению:
проведем преобразование
где
Интегрируя дважды уравнение (3.9), получим
где А и В - коэффициенты определяемые из начальных условий. Уравнение (3.10) соответствует гармоническим колебаниям с периодом Так как колебания ротора были свободными, то частота колебаний будет называться собственной частотой колебаний ротора. Таким образом, мы получили, что значение критической частоты вращения ротора Проведем исследование динамической устойчивости вращающегося вертикального вала с диском, размещенным в его середине с эксцентриситетом. Предположим, что центр прогиба вала (точка W), центр тяжести диска (точка S) и центр опор (точка О) не лежат на одной прямой рис. 3.3.
Рис.3.3. К исследованию динамической устойчивости Обозначим угол наклона прямой OW c осью Х через В соответствии с обозначениями рис.3.3. запишем
Проекции на оси х и r силы упругости со стороны вала
Запишем уравнения движения центра тяжести диска
Продифференцируем дважды выражения (3.11) по времени
Подставим две последние зависимости (3.13) в уравнения (3.12)
По теореме моментов количества движения - момент всех сил, действующих на диск равен вращающему моменту
где Момент количества движения относительно начала координат складывается из
где Подставим выражения (3.16) в уравнение (3.15)
используя соотношения (3.11) и (3.13) и, проведя преобразования, получим
Нелинейные дифференциальные уравнения (3.14) и (3.17) полностью определяют движение диска. Рассмотрим решение для диска, вращающегося с постоянной угловой скоростью
Уравнения (3.14) и (3.17) запишутся
Используя выражения (3.18) преобразуем уравнения (3.19)
Каждое из уравнений (3.18) является уравнением вынужденных колебаний системы с одной степенью свободы, так как проекции центробежных сил на оси При частотах вынужденных колебаний
Первые слагаемые в выражениях (3.21) описывают свободные колебания с частотой Свободные колебания из-за сопротивлений (трения диска о воздух, гистерезиса материала вала и т.д.) являются затухающими, поэтому в выражениях (3.21) первые слагаемые можно опустить, тогда
Подставляя выражения (3.22) в (3.20) получаем, что Величина прогиба вала определяется
Подставим в формулу (3.23) соотношения (3.22) получим
Данное выражение полностью идентично формуле (3.4) так как Подставляя в уравнения (3.22) значения координат Таким образом получено, что при вращении ротора с постоянной угловой скоростью точки О,W,S – располагаются на одной прямой. При критической скорости вращения При
Подставляя (3.25) в формулу (3.23), получим
Таким образом, получено, что на резонансных режимах прогиб растет со скоростью Устойчивость вращения ротора двигателя рассмотрим по графической зависимости рис. 3.4. Ось абсцисс – прогиб
Рис. 3.4. Графическая интерпретация устойчивости ротора
Зависимости При Таким образом ротора, вращающиеся с угловыми скоростями С увеличением угловой скорости вращения ротора При увеличении угловой скорости вращения ротора и сохранении центробежной силы при нулевом прогибе за счет снижения дисбаланса me увеличивается угол наклона прямой При дальнейшем увеличении скорости вращения ротора При сдвиге фаз собственных колебаний, характеризуемых прогибом у, и колебаний, возникающих от действия возмущающей силы, обусловленной действием центробежной силы от дисбаланса еm можно записать уравнение
При При резонансе При скоростях вращения ротора
Из (3.27) следует, что с увеличением угловой скорости вращения ротора при Угловые скорости вращения роторов на рабочих режимах не должны быть близки к критическим скоростям. Для жестких роторов рабочие скорости должны быть меньше, а для гибких больше критических скоростей. Диапазон скоростей, в котором не должны лежать рабочие скорости определяется допустимым прогибом вала. Значение прогиба определяет радиальные зазоры между роторными и статорными частями двигателя, вибрационные перегрузки при прохождении критических скоростей. Диапазон недопустимых скоростей вращения роторов на рабочих режимах определяется из зависимости относительного прогиба от соотношения скоростей, без учета знака прогиба рис.3.5
Рис.3.5. Определение границ допустимых перегрузок Если ограничить относительный прогиб пятикратным значением ( При изготовлении двигателей необходимо стремиться добиваться минимального значения дисбаланса Допустим, что эксцентриситета нет (
3.2 УСТОЙЧИВОСТЬ БЫСТРОВРАЩАЮЩИХСЯ ГЛАДКИХ ВАЛОВ
Расчетная схема вала (Рис. 3.6), представляет из себя идеально уравновешенный вал круглого сечения, расположенный на двух шарнирных опорах и вращающийся с угловой скоростью
Рис. 3.6. Расчетная схема вращающегося упругого вала
Поперечное сечение вала Задача об устойчивости вала сводится к определению угловой скорости вращения вала Оси координат ху связаны с валом и вращаются вместе с ним с угловой скоростью Рассмотрим изогнутый участок вращающегося вала длиной Составим уравнение равновесия сил и моментов
где
Исключим из уравнений (3.28)
Изгибающий момент в любом сечении вала пропорционален кривизне центральной оси вала и определяется по равенству
Для согласования знака кривизны и знака изгибающего момента (рис. 3.6) в формуле (3.31) знак минус. Подставим в уравнения (3.30) зависимости для
Решение уравнения (3.32) дает линию прогиба вала переменного сечения по длине при потере устойчивости. Для проведения анализа зависимости (3.32) рассмотрим вал постоянного поперечного сечения
где
Общее решение уравнения (3.33) имеет вид
Постоянные интегрирования в уравнении (3.35) определяются по условиям закрепления по концам вала. Для расчетной схемы (рис.3.6.) имеем
Согласно (3.31) при нулевом моменте вторая производная прогиба также равна нулю. Условия закрепления левого конца вала ( Условия закрепления правого конца вала (
Отсюда
Равенство (3.37) удовлетворяется решением
где При найденных значениях
Формула (3.39) показывает, что возможно круговое движения вала с прогибом в виде синусоид и произвольным значением амплитуд Найденные формы изгиба могут возникнуть только при определенных угловых скоростях вала, которые определятся из формулы (3.34) при подстановке полученных значений
Рис. 3.7. Формы колебаний двухопорного вала
Критические скорости вращения вала постоянного сечения определенные по формуле (3.40) называются критическими, на этих скоростях вал теряет несущую способность и может неограниченно прогибаться под действием неуравновешенной массы. Как показывают анализ формул (3.39) и (3.40), вал имеет бесчисленное множество критических скоростей и соответствующим им форм изгиба. Кратность критической скорости Обычно при анализе рассматривают первые формы колебаний. Аналогично, используя граничные условия закрепления валов в опорах, можно получить зависимости для расчета критических скоростей вращения валов с другой заделкой в опорах. Не выполняя вывода приведем формулы для расчета критических скоростей вращения для следующих схем закрепления валов: - вал, закреплён одним концом в подшипнике и свободно опирающийся на другой подшипник.
- консольный вал с жёсткой заделкой в подшипнике одним концом. Первая критическая угловая скорость
Критические скорости вращения валов зависят от способа заделки в опорах и определяются материалом вала, расстоянием между опорами и геометрическими размерами вала.
3.3. КРИТИЧЕСКИЕ СКОРОСТИ ВРАЩЕНИЯ РЕАЛЬНЫХ РОТОРОВ В реальном двигателе вал располагается горизонтально и под действием веса диска неподвижный вал получает статический прогиб При вращении вала относительно упругой линии Так как по определению жесткость
Рис.3.8. Влияние массы диска на прогиб вала
откуда
Таким образом, зная статический прогиб, обусловленный массой диска можно определить критические скорости вращения ротора и, наоборот, задаваясь критической скоростью, можно определить допустимый статический прогиб от массы диска а, следовательно, и жёсткость вала. Оценку критической скорости вращения двухопорного ротора, без учёта веса вала можно провести по зависимости:
где
Статические прогибы наиболее распространённых схем роторов можно рассчитать по известному весу диска
Рис. 3.9. Расчетные зависимости статических прогибов вала различных схем
Факторы, влияющие на критические скорости вращения Влияние на критические скорости вращения различных факторов можно провести, анализируя зависимости статических прогибов реальных валов (рис. 3.9). При увеличении статического прогиба снижается критическая скорость вращения. К увеличению статического прогиба приводит увеличение расстояния между опорами, уменьшение жесткости вала, жёсткое закрепления вала в опорах, увеличение массы дисков и т.д. Упругость опор также сказывается на критической скорости вращения ротора. Рассмотрим расчётную схему рис.3.10. Вал с одним диском установлен на опоры А и В. Опора А жёсткая, опора В - упругая. Под действием веса диска неподвижный вал прогибается на величину
а суммарный прогиб с учетом статического прогиба составит:
Рис. 3.10. Влияние упругости опоры на критическую скорость
Продольные растягивающие осевые силы уменьшают статический прогиб а, следовательно, увеличивает критическую скорость вращения ротора. Учёт действия осевой силы можно оценить по зависимости:
где
Крутящий момент, действующий на вал, снижает критическую скорость вращения вала. Влияние крутящего момента на критическую скорость можно оценить по зависимости
где М – приложенный крутящий момент;
где
3.4. ВЛИЯНИЕ ГИРОСКОПИЧЕСКОГО МОМЕНТА НА КРИТИЧЕСКИЕ СКОРОСТИ ВРАЩЕНЯ
Рассмотрим расчётную схему (рис.3.11). Вал шарнирно установлен в опорах А и В и на конце имеет консольный диск. Под действием веса диска вал изогнется и займет криволинейное положение.
Рис.3.11. Расчетная схема ротора с учетом гироскопического момента
При вращении ротора ось вращения может совпадать с криволинейной линией вала, при этом угловая скорость вращения вала равна абсолютной скорости вала. При действии внешних факторов упругая криволинейная ось вала может начать вращаться относительно горизонтальной оси ротора с переносной скоростью
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 3711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.01 с.) |

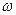 ротора. Ротор, состоящий из вала длиной l посередине которого с эксцентриситетом е насажен тонкий диск массой
ротора. Ротор, состоящий из вала длиной l посередине которого с эксцентриситетом е насажен тонкий диск массой 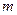 , установлен в опорах А и В. В опоре А жёсткое крепление, в опоре В свободное в продольном направлении крепление вала.Для исключения влияния на прогиб ротора веса вала расположим ротор вертикально (рис.3.1.).
, установлен в опорах А и В. В опоре А жёсткое крепление, в опоре В свободное в продольном направлении крепление вала.Для исключения влияния на прогиб ротора веса вала расположим ротор вертикально (рис.3.1.).
 , вызывающая прогиб вала
, вызывающая прогиб вала  в сторону эксцентриситета от вертикальной оси. При этом, геометрическая ось вала точка W, отклоняется от вертикальной оси также на величину у, а центр масс диска отклонится от вертикальной оси на величину (
в сторону эксцентриситета от вертикальной оси. При этом, геометрическая ось вала точка W, отклоняется от вертикальной оси также на величину у, а центр масс диска отклонится от вертикальной оси на величину (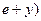 (рис.3.1, б).
(рис.3.1, б).
 . (3.1)
. (3.1)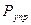
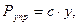 (3.2)
(3.2) (3.3)
(3.3)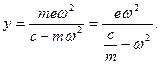 (3.4)
(3.4)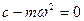 , (3.5)
, (3.5) ).
).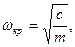 (3.6)
(3.6)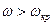 . Проанализируем зависимость (3.4). Для удобства анализа подставим (3.6) в (3.4) и разделим на
. Проанализируем зависимость (3.4). Для удобства анализа подставим (3.6) в (3.4) и разделим на 
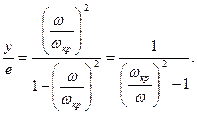 (3.7)
(3.7) и отрицательна при
и отрицательна при  (см. рис.3.1, в).
(см. рис.3.1, в).
 прогиб увеличивается. При
прогиб увеличивается. При 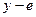 .
.
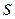 и
и  совмещены рис.3.1, г).
совмещены рис.3.1, г). .
.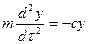 , (3.8)
, (3.8)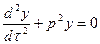 , (3.9)
, (3.9) .
.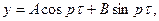 (3.10)
(3.10)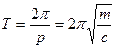 и частотой
и частотой  .
.
 , а угол наклона прямой WS с осью Х, как
, а угол наклона прямой WS с осью Х, как  .
.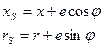 (3.11)
(3.11)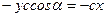 и
и  .
. (3.12)
(3.12)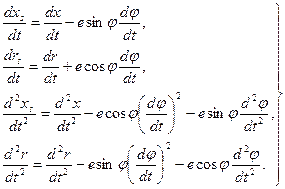 (3.13)
(3.13) (3.14)
(3.14) , (3.15)
, (3.15)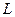 - момент количества движения диска относительно начала координат;
- момент количества движения диска относительно начала координат;  - момент всех сил, действующих на диск.
- момент всех сил, действующих на диск.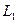 - момента количества движения диска относительно центра тяжести S и
- момента количества движения диска относительно центра тяжести S и 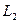 - момента количества движения относительно начала координат О массы
- момента количества движения относительно начала координат О массы  , (3.16)
, (3.16)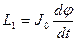 ;
; 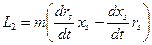 ;
; 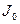 - полярный момент инерции диска.
- полярный момент инерции диска.
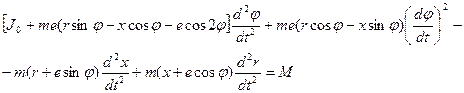 (3.17)
(3.17)
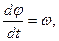
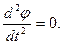
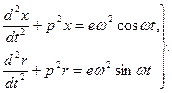 (3.18)
(3.18) (3.19)
(3.19)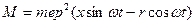 (3.20)
(3.20) и
и  изменяются во времени по периодическому закону с частотой
изменяются во времени по периодическому закону с частотой  Таким образом мы получили, что движение точки W в плоскостях
Таким образом мы получили, что движение точки W в плоскостях  и
и 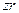 (
(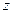 - ось вала) колебательное.
- ось вала) колебательное.
 , общие интегралы уравнений (3.18) запишутся
, общие интегралы уравнений (3.18) запишутся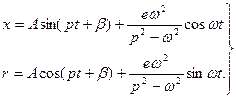 (3.21)
(3.21) (3.22)
(3.22) . Таким образом, после затухания свободных колебаний, при установившемся движении
. Таким образом, после затухания свободных колебаний, при установившемся движении 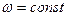 и отсутствии сопротивлений вращающий момент равен нулю, то есть вращение вала устойчиво при любых скоростях вращения, кроме
и отсутствии сопротивлений вращающий момент равен нулю, то есть вращение вала устойчиво при любых скоростях вращения, кроме  .
.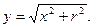 (3.23)
(3.23)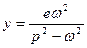 (3.24)
(3.24) Следовательно, сложение колебаний в плоскостях
Следовательно, сложение колебаний в плоскостях 
 и используя соотношение (3.24), получаем
и используя соотношение (3.24), получаем 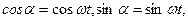 откуда следует, что
откуда следует, что 
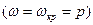 , возникает резонанс при котором прогибы резко возрастают.
, возникает резонанс при котором прогибы резко возрастают.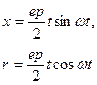 (3.25)
(3.25)
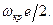
 - прямая выходящая из начала координат под углом
- прямая выходящая из начала координат под углом 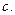

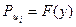 представляют собой прямые, выходящие из точек на оси ординат на расстоянии
представляют собой прямые, выходящие из точек на оси ординат на расстоянии 
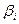 равен
равен 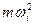 . Точки пересечения прямых -
. Точки пересечения прямых -  и
и  , так как в них
, так как в них 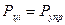 .
.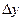 возникает восстанавливающая сила
возникает восстанавливающая сила 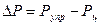 , которая возвращает ротор в равновесное положение (точка В). Также и при уменьшении прогиба на величину
, которая возвращает ротор в равновесное положение (точка В). Также и при уменьшении прогиба на величину 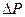 , вследствие
, вследствие 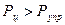 .
.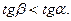
 прямые центробежных сил
прямые центробежных сил  углы наклона прямых
углы наклона прямых 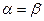 ), то есть прямые параллельны. Во всем диапазоне изменения
), то есть прямые параллельны. Во всем диапазоне изменения 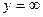 нет пересечения прямых
нет пересечения прямых 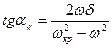 (3.26)
(3.26) . При
. При  и
и  угол сдвига фаз
угол сдвига фаз 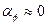 . При колебаниях без сопротивления,
. При колебаниях без сопротивления, 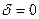 ,
, 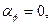 взаимное расположение центра тяжести и центра вращения соответствует рис.3.1, а.
взаимное расположение центра тяжести и центра вращения соответствует рис.3.1, а. (при любом значении коэффициента затухания колебаний
(при любом значении коэффициента затухания колебаний  угол сдвига фаз
угол сдвига фаз 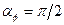 ).
). Если
Если  , то
, то  (рис.3.1, б). При этом, согласно уравнения (3.7), в котором при
(рис.3.1, б). При этом, согласно уравнения (3.7), в котором при 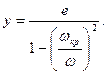 (3.27)
(3.27)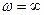 прогиб
прогиб  . То есть при вращении роторов с угловыми скоростями
. То есть при вращении роторов с угловыми скоростями 
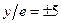 ), то угловая скорость вращения на рабочих режимах не должна находиться в пределах (0.92…1.12)
), то угловая скорость вращения на рабочих режимах не должна находиться в пределах (0.92…1.12)  для увеличения диапазона угловых скоростей с допустимыми перегрузками и меньшего значения прогибов при рабочих режимах.
для увеличения диапазона угловых скоростей с допустимыми перегрузками и меньшего значения прогибов при рабочих режимах. ), тогда прямые
), тогда прямые 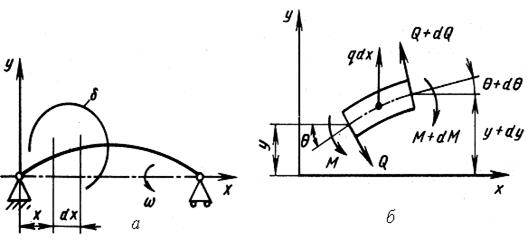
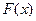 и моменты инерции на изгиб
и моменты инерции на изгиб 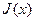 изменяются вдоль его длины. Центры масс сечений лежат на оси вала.
изменяются вдоль его длины. Центры масс сечений лежат на оси вала.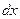 и действующие на него внутренние и внешние силы.
и действующие на него внутренние и внешние силы.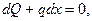
 (3.28)
(3.28)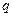 - интенсивность инерционной радиальной нагрузки вала
- интенсивность инерционной радиальной нагрузки вала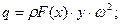 (3.29)
(3.29) - плотность материала.
- плотность материала. , получим связь изгибающего момента с интенсивностью инерционной радиальной нагрузкой
, получим связь изгибающего момента с интенсивностью инерционной радиальной нагрузкой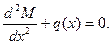 (3.30)
(3.30) (3.31)
(3.31)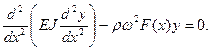 (3.32)
(3.32) и введем относительную координату
и введем относительную координату  . Уравнения (3.32) запишется:
. Уравнения (3.32) запишется: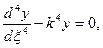 (3.33)
(3.33) (3.34)
(3.34)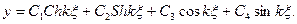 (3.35)
(3.35)
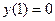
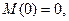
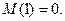
 ):
): 
 .
.
 (3.36)
(3.36)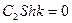 , т.е.
, т.е. 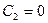 , так как
, так как 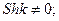
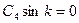 (3.37)
(3.37)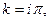 (3.38)
(3.38) - целые числа (1,2,3 и т.д.).
- целые числа (1,2,3 и т.д.).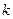 прогиб вала возможен. Форма упругой линии вала, согласно формулы (3.35), определится синусоидой
прогиб вала возможен. Форма упругой линии вала, согласно формулы (3.35), определится синусоидой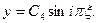 (3.39)
(3.39) . В пределах длины вала
. В пределах длины вала  укладывается целое число полуволн синусоид (рис. 3.7), определяемое числом
укладывается целое число полуволн синусоид (рис. 3.7), определяемое числом 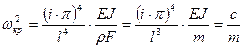 (3.40)
(3.40)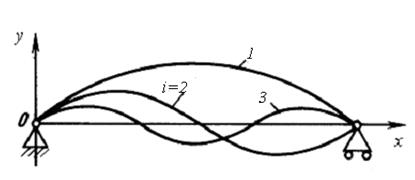
 (
( ).
). . (3.41)
. (3.41)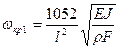 . (3.42)
. (3.42)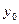 (рис.3.8).
(рис.3.8).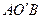 под действием центробежной силы
под действием центробежной силы  Ранее выведенные зависимости будут справедливы и для горизонтального ротора.
Ранее выведенные зависимости будут справедливы и для горизонтального ротора.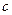 - сила вызывающая единичный прогиб, то можно записать:
- сила вызывающая единичный прогиб, то можно записать: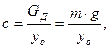 (3.43)
(3.43)
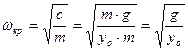 . (3.44)
. (3.44) (3.45)
(3.45)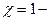 один диск по центру вала;
один диск по центру вала;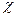 = 1,04 – несколько дисков расположенных симметрично по валу;
= 1,04 – несколько дисков расположенных симметрично по валу;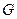 , расстоянию между опорами
, расстоянию между опорами  по зависимостям, приведённым на рис. 3.9.
по зависимостям, приведённым на рис. 3.9.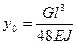 а
а б
б в
в г
г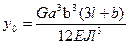 д
д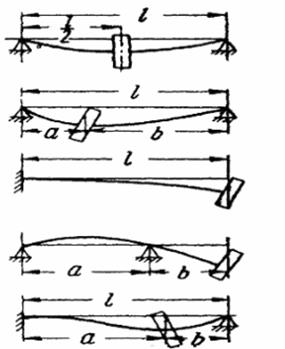
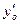 . В то же время, из-за веса диска и ротора, упругая опора В переместится на
. В то же время, из-за веса диска и ротора, упругая опора В переместится на 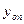 . Тогда дополнительный прогиб ротора в месте размещения диска определится
. Тогда дополнительный прогиб ротора в месте размещения диска определится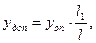 (3.46)
(3.46) (3.47)
(3.47)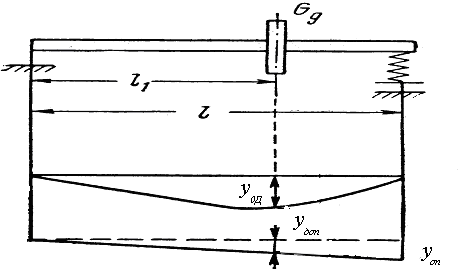
 (3.48)
(3.48)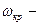 критическая угловая скорость вращения ротора, без учета осевой силы;
критическая угловая скорость вращения ротора, без учета осевой силы;  - осевая сила, действующая на ротор (знак + сила растягивающая, минус – сила сжимающая);
- осевая сила, действующая на ротор (знак + сила растягивающая, минус – сила сжимающая); 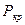 - критическая сила, определяется в зависимости от заделки вала в опорах. Для ротора с шарнирным закреплением в опорах:
- критическая сила, определяется в зависимости от заделки вала в опорах. Для ротора с шарнирным закреплением в опорах: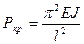 . (3.49)
. (3.49)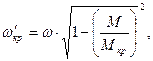 (3.50)
(3.50)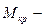 критический крутящий момент, определяемый по зависимости
критический крутящий момент, определяемый по зависимости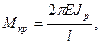 (3.51)
(3.51) - полярный момент инерции сечения вала.
- полярный момент инерции сечения вала.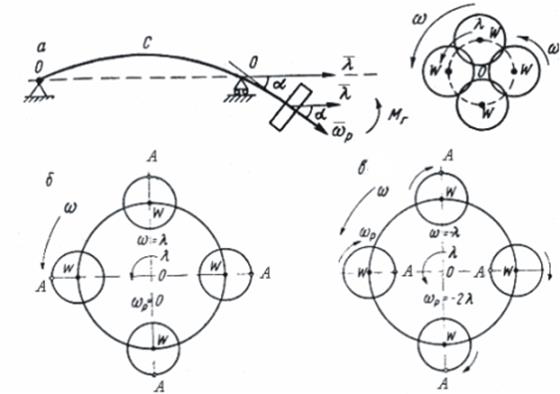
 . Такое движение упругой линии называется прецессионным. В этом случае абсолютная скорость вала будет складываться из относительной скорости
. Такое движение упругой линии называется прецессионным. В этом случае абсолютная скорость вала будет складываться из относительной скорости 


