
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о годографе и кажущейся скорости.Содержание книги
Поиск на нашем сайте
Одним из стержневых понятий в теории сейсморазведки является понятие годографа. Зная положение точек наблюдения, в которых определено время прихода волны, можно составить зависимость t = Рассмотрим такую зависимость для прямой волны вдоль линии наблюдения OS лежащей на плоскости. На этой же плоскости находится источник колебаний (рис45).
Выберем систему координат так, чтобы начало ее находилось в точке возбуждения колебаний О. Такая система наблюдений носит название ОТВ (общей точки возбуждения). Рассматриваемая волна бежит вдоль поверхности от точки O к точке S, координаты которой x и y. Отсюда
а уравнение времени записывают в виде
Из аналитической геометрии следует, что это уравнение конуса вращения. Ось вращения – ось t. Вращением системы координат можно совместить ось x с OS. Тогда y под корнем исчезнет и уравнение будет приведено к виду Поместим на линию наблюдений ОХ несколько сейсмоприемников и зарегистрируем с их помощью волну, годограф которой показан на рис.46. Допустим, что эта волна движется откуда-то из глубины и нам известно положение фронта волны, подошедшей к первому сейсмоприемнику, стоящему в точке Р1. Угол падения волны на линию наблюдения обозначим i. Пусть также известна скорость распространения рассматриваемой волны – V и эта скорость постоянна. Тогда нетрудно получить, воспользовавшись принципом Гюйгенса-Френеля положение фронта волны в точке P2 в момент времени t2 = t1 + Δt. За отрезок времени Δt волна пробежала путь ΔS по лучу К и можно записать, что Δt=

Рис.46. К выводу закона Бенндорфа.
Наблюдателю, находящемуся на поверхности, кажется, что волна, двигаясь от P1 к P2 преодолела расстояние Δх вдоль поверхности наблюдения со скоростью, равной V*= V*= Из сказанного видно, что V* представляет собой дифференциальный параметр или производную годографа. Памятуя о геометрическом смысле производной (тангенс угла наклона касательной к кривой в точке, где мы хотим установить наклон этой кривой) уясним как измерить кажущуюся скорость по любому годографу, если он криволинеен: надо к точке, где мы хотим найти V*, провести касательную и определить тангенс угла ее наклона Δх/Δt. Величина кажущейся скорости зависит от направления подхода волны к поверхности наблюдения (Рис.46,б) Если эта волна движется вдоль поверхности наблюдения, то есть фронт волны перпендикулярен этой поверхности (α = 90°), то из выражения V*= Сказанное означает, что можно по величинам кажущихся скоростей отделять полезные волны от помех, осуществлять их фильтрацию по кажущимся скоростям, или направлению их прихода. Проблема борьбы с помехами чрезвычайно актуальна и составляет главное содержание методики проведения полевых работ и обработки данных. Сами по себе возможности этой борьбы обусловлены тем, что каждая волна характеризуется своими кинематическими зависимостями, то есть формой годографа. Поэтому теория годографа - основной элемент теории сейсморазведки и исследователи заняты решением прямой и обратной кинематических задач сейсморазведки – получением уравнений годографов самых разных волн для самых разных моделей среды и исследованием этих уравнений. Уравнение годографа прямой волны мы уже рассмотрели выше. Остановимся теперь на годографах отраженных и преломленных волн. Для получения уравнения линейного продольного годографа в случае простейшей двухслойной модели среды обратимся к рис. 47.
Пусть произвольный луч падающей волны касается границы в точке R. Из этой точки отражения исходит колебание по лучу RS под углом, равным углу падения (рассматривается монотипная волна). Таким образом, уравнение времени по рассмотренному лучу может быть записано в виде (Рис. 47б)
Буквенную запись необходимо переписать так, чтобы это была зависимость t от х, и параметров модели среды: угла наклона границы, ее глубины и т.д.,. Для вывода уравнения воспользуемся методом зеркальных отображений и проведем ряд дополнительных построений. Рассматривается плоский (двумерный) случай, где все лучи принадлежат вертикальной плоскости, проходящей через профиль наблюдений. Так бывает, когда профиль разбит вкрест простирания пород и границы геологических напластований являются плоскими. Зависимость t(х) выводится в системе с общей точкой возбуждения (ОТВ) в центре расстановки сейсмоприемников (СП), когда колебания возбуждаются в одной точке О, а регистрация волн осуществляется сейсмоприемниками, расставленными по линии –х - +х, проходящей через точку О (продольный профиль). Опустим из точки О нормаль на границу раздела R и продолжим за эту границу до пересечения с продолжением луча RS. Они пересекутся в точке О*, которая является зеркальным отображением О (в зеркале границы R). Это можно доказать из рассмотрения треугольников ОRМ и О*RМ. Нетрудно показать, что они равны. Оба они прямоугольные, МR – общий катет, углы ОRМ и О*RМ равны, поскольку равны углу, дополняющему их до 90°. Следовательно равны катеты ОМ и О*М, представляющие глубину границы по нормали, и гипотенузы ОR и О*R. Таким образом, можно записать, что RS+ RO* = О*S, то есть можно представить лучи, исходящие из пункта возбуждения О через лучи, исходящие из О*. Точка О* называется поэтому мнимым пунктом возбуждения. Итак, уравнение времени можно переписать в таком виде
О*S является гипотенузой большого прямоугольного треугольника О*О'S, где О' – проекция точки О* на линию наблюдения. Следовательно О*S = О'S можно представить как разность х (абсцисса точки S) и х0=ОО'. ОО' – это противолежащий углу φ катет в узком вертикальном прямоугольном треугольнике О*О'O, откуда следует О'О=2h·sinφ. Угол О'О*О равен φ (углу наклона границы),так как это углы с взаимно-перпендикулярными сторонами. Координата точки О* по оси Z обозначена через Z. Тогда можно записать О*S =
и уравнение годографа запишется в виде
Это уравнение гиперболы с минимумом над мнимым пунктом возбуждения. Если положить х=0, то время t0 над точкой возбуждения колебаний (началом координат) окажется равным
При горизонтальном залегании границы R, то есть при равенстве угла φ нулю уравнение годографа отраженной волны примет вид
В этом случае точка минимума гиперболы окажется над пунктом возбуждения, тогда как при наклоне границы R она смещается в сторону восстания отражающей поверхности. Поверхностный (пространственный) годограф ОВ нетрудно получить вращением гиперболы относительно вертикальной оси симметрии (параллельной оси времени), проходящей через точку О1 (рис.47а). Полученная фигура называется гиперболоидом вращения.
Годограф преломленной волны в системе ОТВ также нетрудно вывести, однако мы дадим его запись в готовом виде, а тех, кто затрудняется сделать самостоятельный вывод, адресуем к учебникам в списке литературы.
где с осью времени t пересекутся в одной точке t0 (Рис 48). Если преломляющую границу считать горизонтальной, то есть положить φ=0, годограф преломленной волны примет вид
Геометрически это будут две симметричные ветви, исходящие из t0 с одинаковыми значениями x начальных точек выхода и с одинаковыми значениями времени В кинематической теории распространения волн рассматриваются и исследуются уравнения годографов всех перечисленных выше и иных волн, свидетельствующие об их существенных отличиях, что является основанием для выбора (селекции) этих волн, когда возникает такая необходимость. Определенные возможности такого выбора можно проиллюстрировать, рассмотрев вопрос о соотношении годографов основных типов волн, используемых в сейсморазведке: отраженных, преломленных и прямых все для той же простой двухслойной модели среды и для того же простого двумерного (плоского) случая. Для еще большей простоты положим, что отражающая (преломляющая) поверхность R горизонтальна (Рис.49).
Рис.49. Соотношение годографов основных типов волн.
Выпишем уравнения годографа всех трех, показанных на рис. 49 волн 1) 2) 3)
Чтобы уяснить соотношение годографов прямых и отраженных волн, устремим в выражении для tотр х → ∞. Тогда любым конечным числом в том числе h (и 4h2) в сравнении с ∞ можно будет пренебречь. Следовательно tотр → tпрям, откуда можно заключить, что на бесконечности эти годографы сходятся, неограниченно сближаются. То есть асимптотой годографа отраженной волны (гиперболы) является годограф прямой волны (прямая). Такое соотношение называется асимптотическим приближением. Чтобы уяснить соотношение годографов отраженной и преломленной волн, рассмотрим на рис.49 ситуацию вблизи падения волны под критическим углом. Очевидно, что последний докритический луч отраженной волны и самый первый луч головной практически совпадают (отличаются на бесконечно малую), значит и времена годографов отраженной и преломленной волны будут одинаковыми. Такой случай, когда кривая (гипербола – годограф ОВ) и прямая (годограф преломленной волны) имеют общую точку называется в геометрии касанием. Итак, годограф прямой волны в точке tнач касается годографа ОВ. Наконец, соотношение годографов прямой и преломленной волн – пересечение. Именно так классифицируется случай, когда две прямые на плоскости (плоскости годографа х,t) имеют общую точку. Нетрудно определить координаты этой точки, для чего необходимо приравнять правые части уравнения 1 и 3 положив х = х1.
1) Область, примыкающая к источнику (вплоть до места сближения годографов всех трех волн) – это область работ методом МОВ. Здесь регистрации отраженных волн не мешают головные (они регистрируются на б о' льших удалениях), а от прямых волн отраженные отделены достаточно большим промежутком времени Δt (если граница залегает на глубине более 200-300м) и прямые волны успевают уйти от регистрирующих приборов. При мелком залегании такого промежутка Δt не будет и отраженные волны не удастся проследить уверенно. 2) область больших удалений от источника (>2h)- это пространство, благоприятное для применения МПВ, поскольку преломленные волны регистрируются здесь в первых вступлениях, то есть приходят раньше всех других видов колебаний. Известно, что одной из главных задач, для решения которой применяется методика МПВ, является картирование рельефа поверхности кристаллического фундамента платформенных территорий. Глубина залегания фундамента на территории Восточно-Европейской платформы обычно не превышает 2,5-3 км. Это значит, что для регистрации первых вступлений преломленных волн от поверхности фундамента надо уходить на расстояние более 6-7 км от источника. В то же время, в Прикаспийской впадине, где глубины залегания фундамента оцениваются в 20-25 км, удаление должно составить более 50 км. 3) В области, где сближаются годографы всех волн и регистрируется очень сложная их интерференция (наложение), заниматься сейсмической разведкой вообще не рекомендуется. Таким образом, рассмотренный вопрос о соотношении годографов основных типов волн приобретает отчетливое методическое значение и практический смысл.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.12.181 (0.008 с.) |

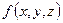 . Зависимость времени прихода волны от координат точек наблюдения называют годографом.
. Зависимость времени прихода волны от координат точек наблюдения называют годографом.
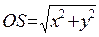 ,
,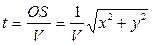 .
.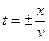 . Это уравнение прямой, исходящей из начала координат. У нее две симметричные относительно оси t ветви:
. Это уравнение прямой, исходящей из начала координат. У нее две симметричные относительно оси t ветви: 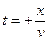 и
и 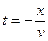 . Такое уравнение называется линейным продольным годографом прямой волны (Рис.45б). Геометрически это сечение конуса вращения (пространственного годографа прямой волны) вертикальной плоскостью, проходящей через начало координат. Непродольный линейный годограф получим, если линия наблюдения не проходит через О. Он будет представлять собой результат вертикального сечения конуса плоскостью, не проходящей через начало координат. Как известно, такое сечение представляет собой гиперболу (рис45а). Здесь точка О' – проекция О на линию профиля l в плоскости XOY. С понятием годографа тесно связано понятие кажущейся скорости V*
. Такое уравнение называется линейным продольным годографом прямой волны (Рис.45б). Геометрически это сечение конуса вращения (пространственного годографа прямой волны) вертикальной плоскостью, проходящей через начало координат. Непродольный линейный годограф получим, если линия наблюдения не проходит через О. Он будет представлять собой результат вертикального сечения конуса плоскостью, не проходящей через начало координат. Как известно, такое сечение представляет собой гиперболу (рис45а). Здесь точка О' – проекция О на линию профиля l в плоскости XOY. С понятием годографа тесно связано понятие кажущейся скорости V*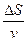
 . Из рисунка видно, что ΔS = ΔхSini, поскольку ΔS -противолежащий углу i катет в образовавшемся на рис.46 прямоугольном треугольнике.
. Из рисунка видно, что ΔS = ΔхSini, поскольку ΔS -противолежащий углу i катет в образовавшемся на рис.46 прямоугольном треугольнике.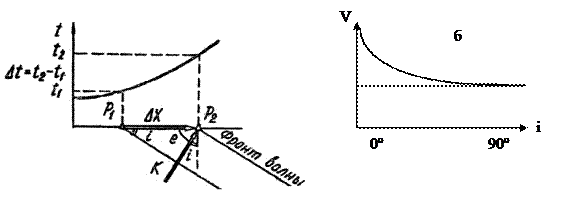
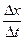 . Если устремить Δх к нулю, то есть перейти к бесконечно малым, то получим V* =
. Если устремить Δх к нулю, то есть перейти к бесконечно малым, то получим V* = 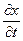 . Такая скорость называется кажущейся V*. Это не скорость перемещения фронта волны, а скорость движения его проекции (его следа) вдоль линии наблюдения. Из приведенной геометрии видно, что связаны эти скорости через Sin i, то есть
. Такая скорость называется кажущейся V*. Это не скорость перемещения фронта волны, а скорость движения его проекции (его следа) вдоль линии наблюдения. Из приведенной геометрии видно, что связаны эти скорости через Sin i, то есть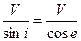 , где е – угол, дополняющий i до 90°. Такой угол называют углом выхода сейсмической радиации. Это выражение носит название закона кажущейся скорости, или закона Бенндорфа.
, где е – угол, дополняющий i до 90°. Такой угол называют углом выхода сейсмической радиации. Это выражение носит название закона кажущейся скорости, или закона Бенндорфа.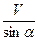 следует, что V*= V (так как sin90°= 1). Так двигаются поверхностные волны-помехи, и определенная по годографам этих волн V* будет как угодно близка к истинной, составляющей в приповерхностной части разреза 500-1000 м/сек. Если же волны приходят снизу, по направлению близкому к вертикали (фронт волны практически параллелен поверхности наблюдения), то V*→∞, поскольку α→0. Так двигаются полезные отраженные волны, откуда следует, что полезные волны те, которые имеют очень высокие кажущиеся скорости, превышающие, как правило, 5000 м/сек.
следует, что V*= V (так как sin90°= 1). Так двигаются поверхностные волны-помехи, и определенная по годографам этих волн V* будет как угодно близка к истинной, составляющей в приповерхностной части разреза 500-1000 м/сек. Если же волны приходят снизу, по направлению близкому к вертикали (фронт волны практически параллелен поверхности наблюдения), то V*→∞, поскольку α→0. Так двигаются полезные отраженные волны, откуда следует, что полезные волны те, которые имеют очень высокие кажущиеся скорости, превышающие, как правило, 5000 м/сек.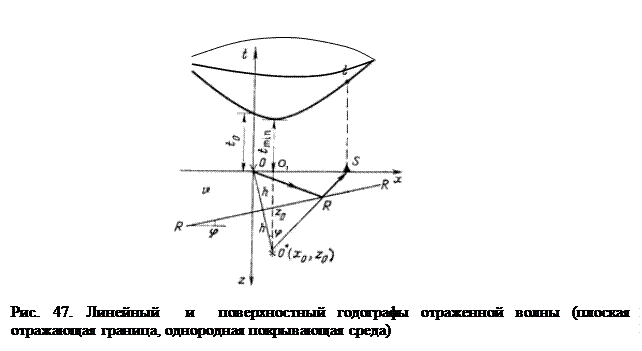
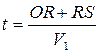 .
.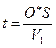
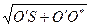 .
.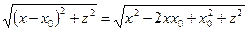 . Поскольку
. Поскольку 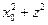 из треугольника О*О'О равно 4h2, выражение для АВ можно переписать так
из треугольника О*О'О равно 4h2, выражение для АВ можно переписать так
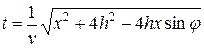
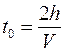
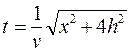
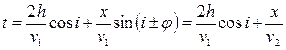 ,
,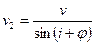 в сторону падения границы, и
в сторону падения границы, и  в сторону ее восстания. V2, то есть скорость скользящей вдоль границы преломленной волны будет равна кажущейся скорости, а кажущиеся скорости по восстанию и падению будут различаться. V2 соответствует граничной скорости Vг если толща 2 однородная и изотропная, в противном случае Vг - как скорость движения волны вдоль напластования (волна бежит в одном и том же слое, подстилающем границу R) не совпадает с V2, характеризующей осредненные свойства среды 2. Приведенное выше уравнение показывает, что линейный продольный годограф преломленной волны представляет собой две прямолинейные ветви, которые будучи продолженными до пересечния
в сторону ее восстания. V2, то есть скорость скользящей вдоль границы преломленной волны будет равна кажущейся скорости, а кажущиеся скорости по восстанию и падению будут различаться. V2 соответствует граничной скорости Vг если толща 2 однородная и изотропная, в противном случае Vг - как скорость движения волны вдоль напластования (волна бежит в одном и том же слое, подстилающем границу R) не совпадает с V2, характеризующей осредненные свойства среды 2. Приведенное выше уравнение показывает, что линейный продольный годограф преломленной волны представляет собой две прямолинейные ветви, которые будучи продолженными до пересечния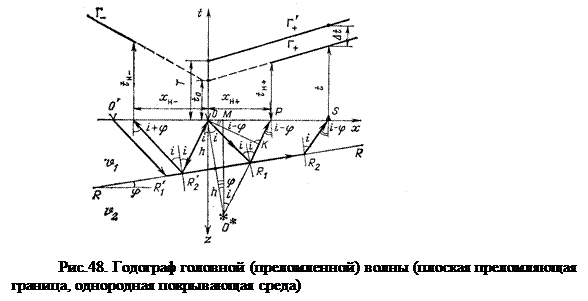

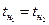 в этих начальных точках.
в этих начальных точках.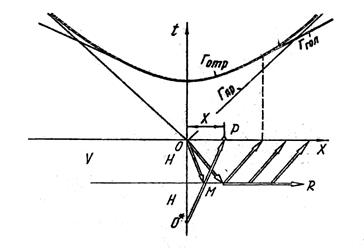
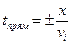
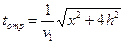
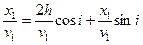 , отсюда
, отсюда 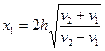 , то есть точка пересечения лежит на расстоянии от начала координат как минимум в два раза большем, чем глубина h исследуемой границы раздела R. Какие же практические выводы можно сделать из рассмотренного соотношения годографов? Их три.
, то есть точка пересечения лежит на расстоянии от начала координат как минимум в два раза большем, чем глубина h исследуемой границы раздела R. Какие же практические выводы можно сделать из рассмотренного соотношения годографов? Их три.


