
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила тяжести и гравитационный потенциал.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гравиразведка – это метод, изучающий аномалии Δgа в распределении естественного поля силы тяжести, обусловленные плотностной неоднородностью земной коры. Т.е. основной физический параметр гравиразведки – плотность, измеряемая в кг/м3 Δgа – это разность значений наблюденного поля gнабл и нормального gо : Δgа ═ gнабл– gо. Нормальное поле в гравиразведке – это такое поле, которое было бы зарегистрировано на поверхности Земли, если бы она представляла собой концентрически однородный сфероид. Такой сфероид принимается за модель Земли в гравиразведке или, иными словами, за теоретическую фигуру Земли. Сфероид близок к сфере, или шару, но отличается некоторой сплюснутостью у полюсов, то есть экваториальный радиус а у него больше полярного b. Это различие составляет примерно 21 км. Международная ассоциация геофизиков установила в 1975 г такие значения этих величин: а = 6378 км; в = 6357 км. Отношение Действие силы тяжести чувствует на себе каждое живое существо и каждое физическое тело на Земле. Оно проявляется в том, что Сила P представляет собой, в основном, равнодействующую двух сил: ньютонианской силы притяжения Землей Fпр, направленной к центру Земли и центробежной силы Fц, т.е.
Участвует в формировании Р и притяжение со стороны других космических тел Fк, но эта величина пренебрежимо мала в сравнении с двумя основными и далее не рассматривается. В гравиразведке действие Р относят к единице массы, то есть притягиваемую массу m в произвольной точке земной поверхности следует принять равной единице. Тогда
Сила, действующая на единицу массы (m = 1) называется напряженностью. Таким образом, величина напряженности численно равна величине ускорения (P=g), то есть по физическому смыслу ускорение можно рассматривать как напряженность. За единицу ускорения принимается, как уже говорилось, величина 1 см/с2 = 1м/с2·10-2, называемая Гал. Название это дано в честь Галилео Галилея, величайшего ученого всех времен и народов. Именно с Галилея, впервые измерившего ускорение свободного падения, а также предложившего и воплотившего в практику идею моделирования, как универсального инструмента исследования, наука стала одной из основополагающих сфер человеческой деятельности. Галилей создал действующую модель Солнечной системы, объяснив с ее помощью механизм движения планет солнечной системы вокруг Солнца и те небесные явления, включая восход, закат, затмения Солнца, которые всегда волновали человечество. Ему же принадлжеит выдающаяся роль в развитии теории гравитации. В гравиразведке в качестве рабочей единицы характеризации поля силы тяжести употребляется миллигал (мГал) 1мГал = 1·10-3Гал Введение в практику разведки этой малой единицы обусловлено тем, что аномалии в распределении поля силы тяжести, вызванные геологическими телами – неоднородностями земной коры – имеют сравнительно небольшую интенсивность, измеряемую единицами или даже десятыми и сотыми долями мГал. Поэтому миллиГал – это достаточно удобная мера их описания. Таким образом, аномалии в распределении силы тяжести измеряют единицами ускорения силы тяжести или свободного падения под действием этой силы. Ускорение – вектор. Поэтому, чтобы не фиксировать каждый раз его направление для характеризации поля употребляют составляющие
Составляющие силы тяжести Остановимся коротко на основных слагаемых силы тяжести
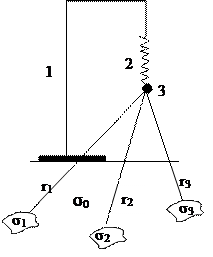
Это всем известное выражение, называемое законом всемирного тяготения Ньютона читается так: две материальные точки в вакууме притягиваются друг другом с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Как и всякий идеальный закон, он приложим только к идеальной практике, к закрытым системам (вакуум, материальные точки и пр.). Такое достижимо только в условиях лабораторного эксперимента, когда можно откачать воздух, свести действующую массу в точку и пр. Для адаптации закона к реальности, к открытым системам, необходимо сделать некоторые существенные допущения, например, считать размеры взаимодействующих масс пренебрежимо малыми в сравнении с расстояниями их взаимодействия, а сами массы концентрически однородными. Для характеризации взаимодействия планет этого будет вполне достаточно. Но при употреблении закона Ньютона для объяснения притяжения измерительного элемента прибора-гравиметра неоднородностями земной коры или Землей в целом, которую трудно принять за однородное тело, он не годится. Приходится дробить неоднородности на бесконечно малые кусочки, в пределах которых можно считать плотность постоянной (то есть использовать дифференциальный подход), затем оценивать по приведенной формуле притяжение измерительного элемента прибора каждым таким кусочком и, наконец, суммировать притяжение этих кусочков, интегрируя по всему замкнутому контуру, по всему объему, занимаемому данной массой – плотностной неоднородностью земной коры или Землей в целом. Идею прибора гравиметра можно представить себе следующим образом: штатив (1), пружинка (2) и грузик (3).
Рис.2.К измерению силы притяжения.
Если поместить такую простую установку на поверхность Земли, грузик будет испытывать притяжение со стороны всех масс-неоднородностей разреза m1,m2 и m3 применительно к ситуации, изображенной на рис.2. То есть все эти массы одновременно повлияют на растяжение пружины 2 грузиком 3 и прибор будет регистрировать суммарное их притяжение. Каждая масса даст в это суммарное притяжение вклад, пропорциональный своей массе, которая равна произведению занимаемого ею объема на эффективную плотность, и обратно пропорциональный квадрату удаления этой массы от измерительного элемента прибора (грузика), находящегося на поверхности Земли. Эффективная плотность σэф1 есть разность плотностей «возмущающего» тела σ1 и вмещающей среды σ0; σэф2 = σ2 - σ0 и σэф3 = σ3 - σ0. Таким образом, каждая неоднородность дает в регистрируемую суммарную величину Fпр вклад тем больший, чем больше ее объем и контрастность плотности σэф и чем меньше глубина ее залегания. В итоге регистрируемая при перемещении прибора вдоль линии наблюдений кривая Fпр может иметь достаточно сложный рельеф, который не всегда очевидно увязывается с картиной распределения источников Fпр . Так, на рис.3 в рельефе кривой виден только один суммарный максимум притяжения, в то время, как источником этого максимума являются не одна, а две неоднородности разреза.

Но вернемся к записи (1) закона тяготения. Здесь представляет интерес коэффициент G, называемый гравитационной постоянной. По своему физическому смыслу G – это сила, действующая между двумя единичными массами m1 и m2, удаленными друг от друга на расстоянии, равном единице длины. То есть, если поместить две сосредоточенные (точечные) массы, каждая из которых равна единице (1 кг) на расстоянии, равном 1 метру, то сила взаимодействия между ними будет равна не единице, а составит 66,7·10-12. Размерность G – Если в адаптированном законе Ньютона положить одну из масс m1 равной единице,а вторую m2 обозначить просто m, то можно записать этот закон в виде F =G и тогда F будет иметь смысл напряженности, то есть силы, отнесенной к единице массы. Если еще раз переписать закон с учетом j, получим запись F=mj, аналогичную таковой для второго закона Ньютона F=ma, где а – ускорение, испытываемое массой m под действием силы F. И, тем самым, убедимся, что напряженность поля притяжения имеет смысл ускорения. Заметим, что Fпр будет зависеть от широты φ точки местности, где находится притягиваемая масса m. Поскольку экваториальный радиус rэ больше rп - полюсного, Fпр достигает максимального значения на полюсе и постепенно уменьшается в направлении экватора. Ускорение, как уже говорилось, векторная величина. Скалярные составляющие j (Fпр) по координатным осям обозначены Fпрx , Fпрy и Fпрz соответственно. Чтобы оценить притяжение m земным сфероидом, его необходимо разбить на точечные массы, то есть массы бесконечно малых размеров dΩ. В результате притяжение сфероида будет определяться, как уже говорилось выше в отношении силы тяжести, интегральной суммой притяжений каждой из находящихся внутри него точечных масс. Однако суммировать их арифметически нельзя, поскольку направления действия этих элементарных сил притяжения разными точечными массами окажутся различными и такое суммирование можно выполнять только раздельно для указанных составляющих по осям x,y,z. Тогда полное значение силы притяжения массы m в точке, где эта масса находится, составит Fпр=
Второе слагаемое силы тяжести Р – центробежная сила Fц. Она определяется суточным вращением Земли вокруг своей оси. Это сила, с которой тело, находящееся под ее действием, стремится улететь от Земли и величина ее определяется угловой скоростью и радиусом вращения. Направлена эта сила по перпендикуляру ρ к оси вращения. Таким образом, Fц= ω2 ·ρ·m, где ρ – радиус вращения, ω – угловая скорость, равная v/ρ; v – линейная скорость. Из этого выражения видно, что на полюсе, где ρ=0, центробежная сила также равна нулю, а максимальное ее значение фиксируется там, где максимума достигает радиус вращения ρ, то есть на экваторе. Составляющих Fц по координатным осям будет только две - Fцx и Fцу, тогда как Fцz окажется равной 0, поскольку проекция Fц на ось Z падает в точку, так как Fц ┴ Z. Таким образом, получается, что Fц не зависит от распределения масс внутри Земли, то есть не участвует в создании аномалии Δg, измеряемой на поверхности Земли, но как мы увидим далее, она учитывается в нормальном поле. Гравитационный потенциал Теперь целесообразно ввести в рассмотрение функцию, называемую гравитационным потенциалом. Напомним, что под потенциалом понимается работа сил поля по перемещению единичной массы из бесконечности в данную точку пространства. Таким образом, потенциал представляет собой меру энергии и выражается в джоулях. Исходя из данного определения, максимальное значение гравитационного потенциала может быть зарегистрировано в центре Земли. Однако, нас интересует в рассматриваемом контексте не столько физический смысл потенциала, сколько его чисто математическая сущность. Дело в том, что от рассмотрения векторов F удобно для характеризации поля перейти к скалярному его описанию. В качестве скалярной функции, через которую определено поле силы тяжести принимается гравитационный потенциал W. Аналитически потенциал определяется как функция, частные производные которой по координатным осям X,Y и Z соответственно равны составляющим силы тяжести:
И в общем случае, то есть в произвольном направлении S: То - есть частные производные потенциала - это проекции силы тяжести на оси координат X, Y и Z или на линию (поверхность) S, по которой перемещается действующая масса m. Вполне понятно, что гравитационный потенциал W является суммой потенциалов притяжения V и центробежной силы U, поскольку сама сила тяжести Р есть векторная сумма силы ньютонианского притяжения Fпр и центробежной силы Fц
то есть W = V + U, где V = G Дифференцируя эти выражения по X,Y и Z нетрудно получить соответствующие выражения для gx, gy, и gz, а также для Fпрx, Fпрy и Fпрz, Fцx и Fцy и убедиться, что Fцz =0, поскольку приведенное выражение для потенциала центробежной силы U не содержит Z. Таким образом, каждой точке пространства соответствует непрерывная, имеющая непрерывные производные, скалярная функция W, производные которой по X, Y и Z являются проекциями силы на соответствующие оси координат. Важно заметить, что вертикальная составляющая gz, учитывая, что Fцz = 0 является частной производной по Z от потенциала притяжения, то есть
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.119.143 (0.011 с.) |

 называется относительным сжатием сфероида. Относительное сжатие как раз и характеризует упомянутую сплюснутость. Итак, если принять, что составляющие нашу планету основные геосферы – ядро и мантия характеризуются разными, но неизменяющимися, то есть постоянными плотностями, а ее фигура имеет сфероидальную форму с относительным сжатием
называется относительным сжатием сфероида. Относительное сжатие как раз и характеризует упомянутую сплюснутость. Итак, если принять, что составляющие нашу планету основные геосферы – ядро и мантия характеризуются разными, но неизменяющимися, то есть постоянными плотностями, а ее фигура имеет сфероидальную форму с относительным сжатием  , то вычисленные на поверхности такого концентрически однородного сфероида значения Δg можно определить как нормальные. Вспомним, что ранее мы условились понимать под нормальным поле над однородным разрезом. Таким образом, Δgо полностью соответствует этому условию. Вполне понятно, что значения нормального поля, вычисленные в разных местах земной поверхности, будут зависеть от широты φ местности. Вычисление gо выполняется по специальным формулам, речь о которых пойдет позднее. В итоге, Δgа = gнабл –gо должно характеризовать именно неоднородность земной коры, поскольку gнабл обусловлено гравитационным действием Земли в целом, а gо представляет долю, обусловленную всеми оболочками, кроме Земной коры.
, то вычисленные на поверхности такого концентрически однородного сфероида значения Δg можно определить как нормальные. Вспомним, что ранее мы условились понимать под нормальным поле над однородным разрезом. Таким образом, Δgо полностью соответствует этому условию. Вполне понятно, что значения нормального поля, вычисленные в разных местах земной поверхности, будут зависеть от широты φ местности. Вычисление gо выполняется по специальным формулам, речь о которых пойдет позднее. В итоге, Δgа = gнабл –gо должно характеризовать именно неоднородность земной коры, поскольку gнабл обусловлено гравитационным действием Земли в целом, а gо представляет долю, обусловленную всеми оболочками, кроме Земной коры.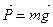 , то есть тело любой массы m притягивается Землей с силой P, зависящей от m и ускорения свободного падения g.
, то есть тело любой массы m притягивается Землей с силой P, зависящей от m и ускорения свободного падения g. =
=  +
+  , (Рис.1)
, (Рис.1)
 становится численно равным g
становится численно равным g
 по координатным осям, то есть скалярные величины gx, gy, gz, называя их соответственно горизонтальными (gx и gy) и вертикальной (gz) компонентами.
по координатным осям, то есть скалярные величины gx, gy, gz, называя их соответственно горизонтальными (gx и gy) и вертикальной (gz) компонентами.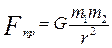 (1)
(1)
 . Откуда взялась эта константа, какова ее природа не совсем понятно. Известно только, исходя из концепции происхождения и становления Вселенной, именуемой концепцией Большого взрыва, что в процессе расширения Вселенной в период от 10-35 до 10-33 секунды происходит фазовый переход, в процессе которого вакуумное состояние посредством туннельного эффекта превращается в горячую плотную Вселенную [10]. Вселенная при этом распадается на отдельные области, одна из которых приобретает свойства четырехмерного пространства – времени. В таком переходе вследствие спонтанного нарушения симметрии единое взаимодействие расчленяется и гравитация отделяется от трех остальных взаимодействий. Тем самым силы гравитации определяют формирование Вселенной буквально с момента ее зарождения, а константа G становится одной из четырех основных мировых констант (остальные три – это постоянные Больцмана, Планка и скорость света), на пересечении которых стоит современный мир и существует человек (антропный принцип). Формулировка антропного принципа, связанного с происхождением Вселенной, как раз и состоит в том, что сложность наблюдаемой Вселенной определяется очень узким диапазоном сечений первичных элементарных процессов и значениями фундаментальных констант. «Если бы сечения элементарных процессов в эпоху Большого взрыва были бы, скажем, немного больше, то вся Вселенная «выгорела» бы за короткий промежуток времени» [10]. Все это дает основания некоторым мыслителям считать, что в этих физических константах и, в частности, в гравитационной, заключается доказательство присутствия Господа Бога на Земле и его замысла о человеке, о предназначении человечества.
. Откуда взялась эта константа, какова ее природа не совсем понятно. Известно только, исходя из концепции происхождения и становления Вселенной, именуемой концепцией Большого взрыва, что в процессе расширения Вселенной в период от 10-35 до 10-33 секунды происходит фазовый переход, в процессе которого вакуумное состояние посредством туннельного эффекта превращается в горячую плотную Вселенную [10]. Вселенная при этом распадается на отдельные области, одна из которых приобретает свойства четырехмерного пространства – времени. В таком переходе вследствие спонтанного нарушения симметрии единое взаимодействие расчленяется и гравитация отделяется от трех остальных взаимодействий. Тем самым силы гравитации определяют формирование Вселенной буквально с момента ее зарождения, а константа G становится одной из четырех основных мировых констант (остальные три – это постоянные Больцмана, Планка и скорость света), на пересечении которых стоит современный мир и существует человек (антропный принцип). Формулировка антропного принципа, связанного с происхождением Вселенной, как раз и состоит в том, что сложность наблюдаемой Вселенной определяется очень узким диапазоном сечений первичных элементарных процессов и значениями фундаментальных констант. «Если бы сечения элементарных процессов в эпоху Большого взрыва были бы, скажем, немного больше, то вся Вселенная «выгорела» бы за короткий промежуток времени» [10]. Все это дает основания некоторым мыслителям считать, что в этих физических константах и, в частности, в гравитационной, заключается доказательство присутствия Господа Бога на Земле и его замысла о человеке, о предназначении человечества.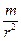 ·1= j
·1= j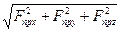
 = gx = g
= gx = g  ;
; 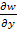 = gy = g
= gy = g  ;
;  = gz = g
= gz = g 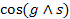
 = gs = g
= gs = g  ; U =
; U =  (x2ω2 + y2ω2)
(x2ω2 + y2ω2)



