
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 5. 1 гравитационное поле, его напряжённостьСодержание книги
Поиск на нашем сайте Гравитацией (или тяготением) называется универсальное взаимодействие (притяжение) между любыми видами материи. Гравитационные силы. Гравитационные силызависят только от взаимных расстояний между взаимодействующими материальными точками. В гравитационном поле, не изменяющемся с течением времени (стационарное гравитационное поле), работа гравитационной силы, действующей на данную перемещающуюся материальную точку, зависит лишь от начального и конечного положений точки и не зависит от формы её траектории. Поэтому гравитационные силы являются потенциальными силами. Гравитационные силы, направлены вдоль линии, соединяющей взаимодействующие точки, и поэтому называются центральными силами.
Гравитационная сила притяжения (сила тяжести) сообщает телу ускорение. Это ускорение называется ускорением свободного падения
Весом тела называется сила, с которой оно действует вследствие тяготения к Земле на опору или подвес, удерживающие его от свободного падения. При этом предполагается, что тело и опора (или подвес) неподвижны относительно системы отсчёта, в которой определяется вес тела. Если тело вместе с опорой свободно падает, то его вес будет равен нулю. Исчезновение веса при движении опоры с ускорением свободного падения называется невесомостью. Состояние невесомости наблюдается в самолёте или космическом корабле при движении с ускорением свободного падения независимо от направления и значения модуля скорости их движения.
При ускоренном движении тела и опоры с ускорением, направленным вертикально вверх, вес тела будет больше действующей на него силы тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты, как при взлёте космической ракеты, так и на участке торможения космического корабля при входе в плотные слои атмосферы. Вес любого тела – наибольший на полюсе и наименьший на экваторе. Кроме того, вес любого тела на некоторой высоте над Землёй меньше, чем на поверхности Земли. Разница в весе одного и того же тела в различных местах Земли или при подъёме на небольшую высоту невелика и практически неощутима. Величина гравитационной силы определяется законом всемирного тяготения, сформулированным И. Ньютоном. Закон всемирного тяготения: между двумя материальными точками действуют силы взаимного притяжения (силы тяготения, гравитационные силы), прямо пропорциональные массам этих точек и обратно пропорциональные квадрату расстояния между ними. Модуль силы тяготения определяется выражением:
где
Закон всемирного тяготения в указанной форме справедлив не только для двух материальных точек, но и для: а) тел произвольной формы, размеры которых во много раз меньше расстояний между центрами масс тел; б) тел со сферически-симметричным распределением масс. В этих случаях Закон всемирного тяготения был открыт И. Ньтоном на основании основных законов динамики и законов Кеплера. Основные законы динамики мы рассмотрели выше, а теперь сформулируем законы Кеплера. § Планеты движутся по эллиптическим траекториям, в одном из фокусов которых находится Солнце. § Радиус-вектор планеты за равные промежутки времени занимает одинаковые площади. § Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Каждое тело (например, Земля) создаёт вокруг себя силовое поле – поле тяготения. Напряжённость этого поля
Напряжённость Как мы видим, напряжённость гравитационного поля совпадает по величине, направлению и единицам измерения с ускорением свободного падения, но, несмотря на это, по своему физическому смыслу это совершенно разные физические величины. В то время как напряжённость поля характеризует состояние пространства в данной точке, сила и ускорение появляются только тогда, когда в данной точке находится пробное тело. Модуль напряжённости гравитационного поля тела (материальной точки) с массой
Эта формула справедлива и в тех случаях, когда источником гравитационного поля является однородное по плотности тело сферической формы. При этом расстояние отсчитывается от центра масс тела, а радиус поверхности тела должен быть меньше этого расстояния. Гравитационные поля удовлетворяют принципу суперпозиции полей: при наложении нескольких гравитационных полей их напряжённости в каждой точке пространства складываются геометрически, т.е. напряжённость результирующего поля
где
I.5.2 ПОТЕНЦИАЛ ПОЛЯ В силу потенциальности гравитационного поля можно ввести его энергетическую характеристику – потенциал. Потенциалом гравитационного поля называется скалярная величина
Потенциал не зависит от массы материальной точки, а является функцией координат точек гравитационного поля. Например, потенциал гравитационного поля, создаваемого неподвижной материальной точкой массы
где Из формулы (I.131) вытекает, что геометрическое место точек с одинаковым потенциалом образуют сферическую поверхность Если потенциал гравитационного поля, создаётся произвольной системой из
При пользовании формулой (I.132) необходимо, чтобы начала отсчётов потенциалов Существует взаимосвязь между потенциалом поля тяготения и его напряжённостью:
Величина Связь между потенциалом поля тяготения и его напряжённостью, можно представить и в другом виде:
где I.5.3 КОСМИЧЕСКИЕ СКОРОСТИ Мы знаем, что тело, брошенное горизонтально с некоторой высоты, движется по параболе и падает на Землю тем дальше, чем больше скорость бросания. При некоторой скорости
В этом уравнении
Скорость Для того чтобы, тело могло выйти из сферы земного притяжения и стало спутником Солнца (т.е. удалилось на такое расстояние, при котором притяжение к Земле становится пренебрежимо малым), ему при запуске с Земли необходимо сообщить скорость Формула для её нахождения имеет вид (она выводится из закона сохранения энергии):
или приняв во внимание формулу (I.136), получим, что И, наконец, для того, чтобы тело покинуло пределы Солнечной системы, ему при запуске с Земли, необходимо сообщить скорость Впервые космические скорости были достигнуты в СССР: первая – при запуске первого искусственного спутника Земли в 1957 г., вторая – при запуске ракеты к Луне в 1959 г. После исторического полёта 12 апреля 1961г. началось бурное развитие как советской, так и зарубежной космонавтики.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |

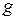 (подробнее о нём см.§I.1.6). Ускорение свободного падения связано с весом тела
(подробнее о нём см.§I.1.6). Ускорение свободного падения связано с весом тела  соотношением:
соотношением: . (I.125)
. (I.125) , (I.126)
, (I.126) и
и  - массы взаимодействующих точек;
- массы взаимодействующих точек; 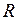 - расстояние между ними. Коэффициент пропорциональности
- расстояние между ними. Коэффициент пропорциональности  - называется гравитационной постоянной. Гравитационная постоянная определяется опытным путём и равна силе взаимодействия двух материальных точек, имеющих единичные массы и находящиеся на единичном расстоянии одна от другой. В системе СИ гравитационная постоянная имеет следующее значение:
- называется гравитационной постоянной. Гравитационная постоянная определяется опытным путём и равна силе взаимодействия двух материальных точек, имеющих единичные массы и находящиеся на единичном расстоянии одна от другой. В системе СИ гравитационная постоянная имеет следующее значение: (Н·м2/кг2).
(Н·м2/кг2). в любой его точке характеризует силу, которая действует на находящееся в этой точке другое тело и представляет собой векторную величину, направление которой определяется направлением гравитационной силы. Напряжённостью поля тяготения называется отношение силы, действующей на тело, помещённое в поле тяготения, к массе этого тела.
в любой его точке характеризует силу, которая действует на находящееся в этой точке другое тело и представляет собой векторную величину, направление которой определяется направлением гравитационной силы. Напряжённостью поля тяготения называется отношение силы, действующей на тело, помещённое в поле тяготения, к массе этого тела. . (I.127)
. (I.127) тела, находящегося в этом месте пространства:
тела, находящегося в этом месте пространства:  .
.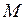 на расстоянии
на расстоянии 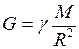 . (I.128)
. (I.128) , (I.129)
, (I.129) - напряжённость
- напряжённость 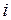 - го поля в рассматриваемой точке пространства.
- го поля в рассматриваемой точке пространства. , равная отношению потенциальной энергии
, равная отношению потенциальной энергии 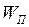 материальной точки, помещённой в рассматриваемую точку поля, к массе
материальной точки, помещённой в рассматриваемую точку поля, к массе 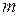 материальной точки:
материальной точки: . (I.130)
. (I.130) , (I.131)
, (I.131) . Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными.
. Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. неподвижных материальных точек, то при наложении гравитационных полей их потенциалы складываются алгебраически, т. е. потенциал
неподвижных материальных точек, то при наложении гравитационных полей их потенциалы складываются алгебраически, т. е. потенциал 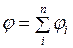 . (I.132)
. (I.132) всех накладывающихся полей были выбраны одинаково:
всех накладывающихся полей были выбраны одинаково:  .
. . (I.133)
. (I.133) характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения и носит название градиента потенциала.
характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения и носит название градиента потенциала. , (I.134)
, (I.134) - градиент скаляра
- градиент скаляра 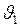 тело вообще может не упасть на Землю, а будет описывать круговые траектории, оставаясь на одной и той же высоте над Землёй. Это случится тогда, когда ускорение, сообщаемое телу силой тяжести, будет равно центростремительному ускорению, необходимому для удержания тела при данной его скорости на круговой орбите, или, иначе говоря, когда сила притяжения тела Землёй будет являться центростремительной силой. Положив радиус орбиты равным радиусу Земли
тело вообще может не упасть на Землю, а будет описывать круговые траектории, оставаясь на одной и той же высоте над Землёй. Это случится тогда, когда ускорение, сообщаемое телу силой тяжести, будет равно центростремительному ускорению, необходимому для удержания тела при данной его скорости на круговой орбите, или, иначе говоря, когда сила притяжения тела Землёй будет являться центростремительной силой. Положив радиус орбиты равным радиусу Земли  . (I.135)
. (I.135) - центростремительное ускорение тела,
- центростремительное ускорение тела,  - сила тяжести, действующая на тело. Из уравнения (I.135) следует, что
- сила тяжести, действующая на тело. Из уравнения (I.135) следует, что . (I.136)
. (I.136) м и
м и  м/с2, она будет равна
м/с2, она будет равна 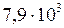 м/с. При запуске спутника непосредственно у поверхности Земли (если бы не было атмосферы, необходимая начальная скорость была бы равна
м/с. При запуске спутника непосредственно у поверхности Земли (если бы не было атмосферы, необходимая начальная скорость была бы равна  км/с).
км/с). , называемую второй космической скоростью.
, называемую второй космической скоростью.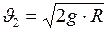 , (I.137)
, (I.137)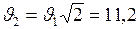 км/с. Значение
км/с. Значение  км/с которая носит название третьей космической скорости. Сообщение телам таких больших начальных скоростей является сложной технической задачей.
км/с которая носит название третьей космической скорости. Сообщение телам таких больших начальных скоростей является сложной технической задачей.


