
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. 3. 1 основные законы и формулыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Работа: а) постоянной силы
где б) переменной силы
где 2. Мощность: а) средняя за промежуток времени
б) мгновенная
где
или
3. Кинетическая энергия точки или тела, движущегося поступательно,
4. Потенциальная энергия тела, поднятого на высоту
5. Потенциальная энергия упругодеформированного тела
6. Закон сохранения механической энергии (для консервативной системы):
7. Работа, совершаемая внешними силами, действующими на тело, и изменение кинетической энергии тела связаны соотношением:
Формула (II.52) представляет собой теорему о кинетической энергии. 8. Закон сохранения импульса. Импульс замкнутой системы есть величина постоянная:
где Для двух взаимодействующих материальных точек, двигающихся по одной прямой, этот закон имеет вид
где
9. Применение законов сохранения энергии и импульса к прямому центральному удару шаров:
а) при центральном неупругом ударе двух тел с массами
б) при центральном упругом ударе тела будут двигаться с различными скоростями. Скорость первого тела после удара
Скорость второго тела после удара
II.3.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.41 Спортсмен, прыгая в высоту, отталкивается от поверхности Земли. Почему в результате такого взаимодействия не ощущается движение Земли? Ответ. Земля имеет очень большую массу, поэтому при взаимодействии её скорость изменяется незначительно.
ЗАДАЧА № II.42 Мог ли в действительности герой книги Э. Распе барон Мюнхгаузен согласно своему рассказу сам вытащить себя и своего коня из болота? Ответ. Нет, такого произойти не могло, так как по закону сохранения импульса внутренние силы системы не могут привести в движение её центр тяжести.
ЗАДАЧА № II.43 Прочитайте отрывок из стихотворения В. Высоцкого: ... Но стрелки я топлю — на этих скоростях песчинка обретает силу пули, — и я сжимаю руль до судорог в кистях: успеть, пока болты не затянули! Почему на больших скоростях даже «песчинка обретает силу пули»? Ответ. При больших скоростях резко увеличивается импульс песчинки.
ЗАДАЧА № II.44 До изобретения парохода существовал проект судна, основанный на следующем принципе: запас воды на судне предполагалось выбрасывать с помощью сильного нагнетательного насоса в кормовой части, вследствие чего судно должно было двигаться вперед. Проект не был осуществлен, однако он сыграл известную роль в изобретении парохода. Как называется этот принцип? Где он используется в современной технике? Ответ. Принцип реактивного движения.
ЗАДАЧА № II.45 Основания настольных вентиляторов всегда снабжают прокладкой из мягкой резины. С какой целью? Ответ. При работе вентилятора в результате взаимодействия его с потоком воздуха возникает сила, которая может сдвинуть вентилятор с места. Резиновая прокладка увеличивает силу трения.
ЗАДАЧА № II.46 Летящая пуля не разбивает оконное стекло, а образует в нем круглое отверстие. Почему? Ответ. Время столкновения пули и стекла очень мало, поэтому деформация стекла под давлением пули не успевает распространиться на стекло. Импульс тела получил небольшой участок стекла.
ЗАДАЧА № II.47 Что должен делать человек, чтобы не провалиться под тонкий лед: бежать по льду или стоять на нем? Ответ. Надо бежать. В этом случае время взаимодействия человека с участком льда, с которым он соприкасается в момент бега, очень мало. Поэтому импульс силы, действующей на лёд, также мал и лёд не успевает разрушиться под ногами человека. ЗАДАЧА № II.48 Почему, направив поток воздуха из воздушного шарика вертикально вниз, шарик можно привести в движение? Что произойдет, если весь воздух выйдет из шарика? Ответ. Воздух, выходящий из шарика, приобретает импульс. Такой же по модулю, но противоположный по направлению импульс получает шарик. Когда весь воздух из шарика выйдет, его импульс станет равным нулю. Нулю будет равен и импульс шарика. Поэтому, имея начальную скорость, шарик будет двигаться как тело, брошенное вертикально вверх.
ЗАДАЧА № II.49 В книге Э. Распе «Приключения барона Мюнхгаузена» читаем: «Обе пушки грянули в один и тот же миг. Случилось то, чего я ожидал: в намеченной мною точке два ядра — наше и неприятельское — столкнулись с ужасающей силой, и неприятельское полетело назад к испанцам... Наше ядро тоже не доставило им удовольствия...» Возможно ли описанное здесь явление? Ответ. Это возможно, если ядро, которым выстрелил барон, имело гораздо большую массу, чем неприятельское.
ЗАДАЧА № II.50 Какую работу нужно совершить, чтобы груз массой 1 кг поднять вначале равномерно на высоту 1м с очень малой скоростью, далее в течение 2 с поднимать равноускоренно с ускорением 0,5 м/с2, а затем – равнозамедленно с ускорением 0,5 м/с2 до полной остановки? Сопротивление воздуха не учитывать. Дано:
Найти: Решение
Полную работу против силы тяжести определим как сумму работ на каждом из участков:
где тогда
Учитывая, что
Подставим уравнения (2), (3) и (4) в формулу (1) и после ряда преобразований, получим:
ЗАДАЧА № II.51 Какова жёсткость буферных пружин вагона, если при скорости Дано: Найти: Решение Очевидно, кинетическая энергия вагона перешла в потенциальную энергию пружин. По закону сохранения энергии для системы вагон – пружина имеем:
Так как мы имеем две буферных пружины и, учитывая, что
где Подставим данные выражения в формулу (2), получим:
Выразим из формулы (3) коэффициент жёсткости пружины
ЗАДАЧА № II.52 Пуля, летящая со скоростью 400 м/с, попадает в вал и проходит до остановки 0,5 м (рис.64). Определить силу сопротивления вала движению пули, если его масса 24 г.
Дано:
Найти: Решение
Работа, совершаемая пулей, по преодолению силы сопротивления вала определяется по формуле:
Так как,
Работа, совершаемая внешними силами, действующими на тело, и изменение кинетической энергии тела связаны соотношением:
Так как пуля остановилась, то
Выразим из формулы (4) силу сопротивления вала движению пули:
ЗАДАЧА № II.53 Тело массой Дано: Найти: Решение
Высота, с которой падало тело, определяется по формуле:
После удара первоначальная механическая энергия уменьшилась на
Подставим формулу (1) в формулу (2), получим:
Тогда согласно закону сохранения энергии:
Подставим формулу (4) в формулу (3) и выразим из неё высоту
ЗАДАЧА № II.54 Определить работу силы тяги при подъёме груза по наклонной плоскости, среднюю мощность и КПД подъёмного устройства, если масса груза 100 кг, длина наклонной плоскости 2м, угол её наклона к горизонту 300, коэффициент трения 0,1, ускорение при подъёме 1 м/с2. У основания наклонной плоскости груз находился в покое. Дано:
Найти: Решение
Работа силы тяги при подъёме груза по наклонной плоскости может быть найдена по формуле:
где
Для определения силы тяги, воспользуемся вторым законом Ньютона. В векторной форме этот закон имеет вид:
где Проецируем обе части уравнения (3) на оси
Решим полученную систему уравнений (4) относительно неизвестного параметра (силы тяги), получим:
Подставим формулу (5) в формулу (2):
Средняя мощность подъёмного устройства, определяется по формуле:
где
Выразим время
Подставим найденные значения По определению КПД подъёмного устройства равен:
где
Подставим найденные значения
ЗАДАЧА № II.55 Насос, двигатель которого развивает мощность 10 кВт, поднимает 15 м3 воды на высоту 10 м за 5 мин. Найти КПД насоса. Дано:
Найти: Решение КПД насоса определим по формуле:
где
Массу воды выразим через плотность
где Подставим формулы (2), (3) и (4) в формулу (1), получим:
ЗАДАЧА № II.56 Шарик массой 100 г падает вертикально на пол с высоты 125 см и упруго отскакивает от него. Найти модуль изменения импульса шарика в момент отскока. Чему равен модуль изменения импульса при неупругом ударе? Дано:
Найти: Решение
Скорость шарика около пола, найдём по формуле:
Так как
Изменение импульса (рис 66), определяется формулой:
При упругом ударе:
Вектор При неупругом ударе:
ЗАДАЧА № II.57 Снаряд массой 100 кг, летящийгоризонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нём. Найти скорость вагона, если он двигался со скоростью 36 км/ч навстречу снаряду.
Дано:
Найти: Решение
а)
б)
Запишем для снаряда и вагона с песком закон сохранения импульса в векторной форме при неупругом ударе:
Возьмём проекцию всех векторных величин на ось
Выразим из формулы (2) скорость вагона после взаимодействия:
Следовательно, направление движения вагона не изменилось.
ЗАДАЧА № II.58 Два глиняных комка массами Дано: Найти:
Решение
б)
Запишем закон сохранения импульса для неупругого соударения:
Так как соударение неупругое, то закон сохранения энергии буде иметь вид:
Считая направление вдоль оси
Исключая скорость
ЗАДАЧА № II.59 Шар массой
Дано: Найти:
Решение
Доля энергии, переданной первым шаром второму, выразится соотношением:
где
Скорость второго шара после взаимодействия
Подставим формулы (2), (3) и (5) в формулу (1), после преобразований, получим:
Из соотношения (6) видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.013 с.) |

 , (II.43)
, (II.43)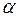 - угол между направлениями силы и перемещения;
- угол между направлениями силы и перемещения; , (II.44)
, (II.44) и
и  - координаты начальной и конечной точек пути.
- координаты начальной и конечной точек пути.
 ; (II.45)
; (II.45) , (II.46)
, (II.46) - работа, совершаемая телом за время
- работа, совершаемая телом за время  ,
, . (II.47)
. (II.47) , или
, или  . (II.48)
. (II.48) , много меньше радиуса
, много меньше радиуса 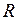 Земли (
Земли (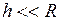 ):
): . (II.49)
. (II.49) . (II.50)
. (II.50) . (II.51)
. (II.51) . (II.52)
. (II.52) или
или  , (II.53)
, (II.53)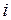 - число материальных точек, входящих в рассматриваемую замкнутую систему.
- число материальных точек, входящих в рассматриваемую замкнутую систему.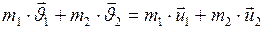 , (II.54)
, (II.54)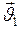 и
и  - скорости точек до их взаимодействия;
- скорости точек до их взаимодействия; и
и  - скорости точек после их взаимодействия.
- скорости точек после их взаимодействия. и
и  общая скорость движения этих тел после удара может быть найдена по формуле
общая скорость движения этих тел после удара может быть найдена по формуле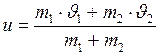 (II.55)
(II.55) . (II.56)
. (II.56) . (II.57)
. (II.57) кг;
кг; м;
м; ;
; с;
с; м/с2;
м/с2; м/с2.
м/с2.
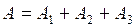 , (1)
, (1)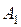 - работа против силы тяжести при равномерном подъёме груза:
- работа против силы тяжести при равномерном подъёме груза: 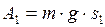 ,
,  ,
, . (2)
. (2)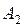 - работа против силы тяжести при равноускоренном подъёме груза:
- работа против силы тяжести при равноускоренном подъёме груза: ,
,  , так как
, так как  (по условию задачи), то
(по условию задачи), то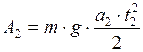 . (3)
. (3)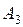 - работа против силы тяжести при равнозамедленном подъёме груза:
- работа против силы тяжести при равнозамедленном подъёме груза:  ,
,  ,
,  , так как
, так как  , то
, то  , следовательно
, следовательно  .
. и
и  , получим:
, получим: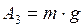
 . (4)
. (4) ;
; 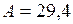 Дж.
Дж. он останавливается на пути
он останавливается на пути  при столкновении его с опорой? Масса вагона равна
при столкновении его с опорой? Масса вагона равна 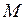 , буферных пружин две.
, буферных пружин две.
 . (1)
. (1) , то уравнение (1), перепишем в виде:
, то уравнение (1), перепишем в виде: , (2)
, (2)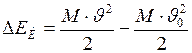 ;
; 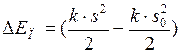 .
.
 . (3)
. (3) и учтём, что
и учтём, что  и
и  :
: .
. м/с;
м/с;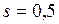 м;
м;
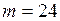 г =
г =  кг.
кг.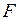 -?
-?
 , попадает в вал
, попадает в вал
 , то
, то  , то формула (1), примет вид:
, то формула (1), примет вид: . (2)
. (2) . (3)
. (3) . С учётом этого, и приравняв формулы (2) и (3), получим:
. С учётом этого, и приравняв формулы (2) и (3), получим: . (4)
. (4) ;
;  кН.
кН.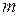 падает на землю за время
падает на землю за время  . При ударе о поверхность выделилась энергия
. При ударе о поверхность выделилась энергия  . Найти высоту, с которой падало тело, и высоту, на которую оно поднялось после удара.
. Найти высоту, с которой падало тело, и высоту, на которую оно поднялось после удара. . (1)
. (1)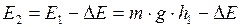 . (2)
. (2)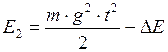 . (3)
. (3) . (4)
. (4) :
: .
. кг;
кг; м;
м; м/с2;
м/с2; рад;
рад; .
.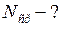

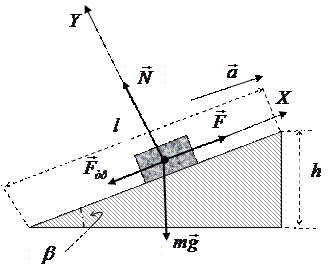
 - сила тяги;
- сила тяги;  (перемещение тела будет равно длине наклонной плоскости);
(перемещение тела будет равно длине наклонной плоскости);  , а
, а 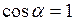 . С учётом этого формулу (1) перепишем в виде:
. С учётом этого формулу (1) перепишем в виде: . (2)
. (2) , (3)
, (3)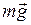 - сила тяжести;
- сила тяжести;  - сила трения;
- сила трения;  - сила нормальной реакции опоры (рис.65).
- сила нормальной реакции опоры (рис.65). и
и  :
: ; (4)
; (4) ;
; .
.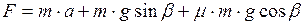 . (5)
. (5) . (6)
. (6) Дж
Дж  кДж.
кДж. , (7)
, (7) , т.к.
, т.к.  , то:
, то: . (8)
. (8) ;
;  с.
с. и
и  Вт.
Вт. . (9)
. (9)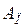 - полезная работа (полезным действием подъёмного механизма является перемещение груза на высоту
- полезная работа (полезным действием подъёмного механизма является перемещение груза на высоту 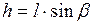 );
); - затраченная работа, она равна работе силы тяги при подъёме груза по наклонной плоскости, т.е.
- затраченная работа, она равна работе силы тяги при подъёме груза по наклонной плоскости, т.е.  кДж.
кДж. ;
;  Дж.
Дж. .
. кВт
кВт 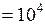 Вт;
Вт; м3;
м3;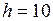 м;
м; мин;
мин; кг/м3.
кг/м3. (2)
(2)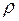 и объём воды:
и объём воды: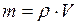 . (3)
. (3) , (4)
, (4) - мощность двигателя;
- мощность двигателя;  %;
%;  %.
%. кг;
кг; см =
см =  м.
м.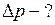

 , (1)
, (1) ;
;  м/с.
м/с. . (2)
. (2)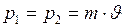 , в проекции на ось
, в проекции на ось 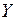 :
: ;
;  кг·м/с.
кг·м/с.
 - направлен вертикально вверх (как и сила упругости, действующая на шарик со стороны пола).
- направлен вертикально вверх (как и сила упругости, действующая на шарик со стороны пола).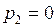 , тогда
, тогда  ;
; кг·м/с.
кг·м/с.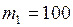 кг;
кг; т =
т =  кг;
кг; м/с;
м/с; км/ч = 10 м/с.
км/ч = 10 м/с.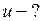

 . (1)
. (1)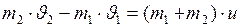 . (2)
. (2) ;
;  м/с.
м/с.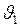 и
и  навстречу друг другу, неупруго соударяются. Найти количество выделившегося тепла
навстречу друг другу, неупруго соударяются. Найти количество выделившегося тепла  (рис. 68).
(рис. 68).
 а)
а) . (2)
. (2) (3)
(3) из системы (3) и выражая количество выделившегося тепла
из системы (3) и выражая количество выделившегося тепла  .
. своей кинетической энергии первый шар передал второму?
своей кинетической энергии первый шар передал второму? .
.
 , (1)
, (1) - кинетическая энергия первого шара до удара. Она равна:
- кинетическая энергия первого шара до удара. Она равна: . (2)
. (2) - кинетическая энергия второго шара после удара. Она равна:
- кинетическая энергия второго шара после удара. Она равна: . (3)
. (3) , найдём, решая совместно систему уравнений (4):
, найдём, решая совместно систему уравнений (4): (4)
(4) . (5)
. (5) . (6)
. (6)


