
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. 4 механика твёрдого телаСодержание книги
Поиск на нашем сайте
II.4.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ 1. Основное уравнение динамики вращательного движени я: а) в общем случае
где
б) в случае постоянных момента силы и момента инерции
в) в случае постоянного момента инерции
где 2. Момент импульса материальной точки
или
где 3. Момент силы относительно оси вращения
где
где
4. Момент инерции: а) материальной точки
б) твёрдого тела
где
Если тело однородно, т.е. его плотность
где интегрирование ведётся по всему объёму тела в) моменты инерции тел простейшей формы относительно некоторых осей рассмотрены в главе I.4, § I.4.1. 5. Теорема Штейнера. Момент инерции тела
где
6. Закон сохранения импульса: а) в общем виде
где 7. Работа постоянного момента силы, действующего на вращающееся тело:
где 8. Мгновенная мощность, развиваемая при вращении тела:
9. Кинетическая энергия вращающегося тела:
10. Кинетическая энергия тела, катящегося по плоскости без скольжения:
где
11. Связь между работой, совершаемой при вращении тела и изменением его кинетической энергии:
12. Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения.
Эта аналогия приведена в таблице 2 (глава I.4, § I.4.3.) II.4.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ЗАДАЧА № II.58 При наличии трения обруч скатывается с наклонной плоскости, а при отсутствии – скользит по ней. В каком случае и во сколько раз скорость, которую будет иметь обруч у основания наклонной плоскости, больше? Ответ. При скольжении без трения скорость больше в 1,4 раза.
ЗАДАЧА № II.59 Катушка находится на столе рисунок 69. В какую сторону она будет двигаться, если нить натягивается силой (продолжение линии действия силы
Ответ. Действие момента силы
ЗАДАЧА № II.60 Каким образом легче сдвинуть автомобиль с места: прикладывая силу к кузову автомобиля или к поверхности шины по касательной к ней? Ответ. Легче сдвинуть автомобиль, прикладывая силу к поверхности шины по касательной в верхней точке колеса. При этом плечо силы равно ЗАДАЧА № II.61 На поверхности воды плавает деревянная пластинка, к которой прилагается пара сил (две равные антипараллельные силы, не действующие по одной прямой) в горизонтальном направлении. Относительно какой точки, поворачивается пластинка? Ответ. Пара сил вызовет вращение пластинки вокруг её центра масс. Указание. Так как сумма действующих на пластинку сил равна нулю, то центр масс её будет покоиться. ЗАДАЧА № II.62 Планета движется вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце. Доказать, что момент количества движения планеты относительно Солнца есть величина постоянная. Ответ. Согласно основному закону динамики вращательного движения:
ЗАДАЧА № II.63 Известно, что для того чтобы отличить сырое яйцо от сваренного вкрутую, достаточно попытаться закрутить его на столе. Варёное яйцо крутится долго. Сырое же раскрутить не удаётся. Объяснить, на чём основан этот способ. Ответ. Яйцо, сваренное вкрутую, вращается как твёрдое тело, сырое – как сосуд, наполненный жидкостью; сообщая скорлупе вращение, мы ещё не сообщаем вращения всем частицам жидкости.
ЗАДАЧА № II.64 Какая из форм конца вала, изображённых на рисунке 70, а и б, выгоднее (при равных силах давления на опору и скоростях вращения) с точки зрения уменьшения потерь на трение при вращении вала в опорном подшипнике. (Трением о боковые стенки можно пренебречь).
а) б)
ЗАДАЧА № II.65 В какихслучаях момент импульса и угловая скорость вращающегося тела коллинеарные? Ответ. При вращении тела вокруг одной из его главных осей инерции.
ЗАДАЧА № II.66 В каких случаях кинетическая энергия вращающегося тела Ответ. При вращении тела вокруг одной из его главных осей инерции.
ЗАДАЧА № II.67 В каких случаях основное уравнение динамики вращательного движения может быть представлено в виде: Ответ. Если: а) тело является шаровым волчком, б) векторы
ЗАДАЧА № II.68 Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг (рис. 71). С каким ускорением будет опускаться гиря, если её предоставить самой себе?
Дано:
Найти: Решение
Линейное ускорение гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности, и связано с угловым ускорением вала соотношением:
где Угловое ускорение вала может быть выражено основным уравнением динамики вращающегося тела:
где
Рассматриваем вал как однородный цилиндр. Тогда его момент инерции относительно геометрической оси:
Вращающий момент, действующий на вал, равен произведению силы натяжения шнура на радиус вала:
где Силу натяжения шнура найдём из второго закона динамики. На гирю действуют две силы: сила тяжести ( Направление вектора ускорения ( Запишем второй закон Ньютона в векторной форме:
Проецируем обе части уравнения (5) на ось
Выразим из уравнения (6) силу натяжения нити и подставим в формулу (4), получим:
Подставим формулы (7) и (3) в формулу (2) и после небольшого преобразования, получим:
Найденное выражение (8) для углового ускорения, подставим в формулу (1) и после ряда преобразований, получим формулу для нахождения линейного ускорения гири:
ЗАДАЧА № II.69 К ободу диска массой 5 кг приложена касательная сила 19,6 Н. Какую кинетическую энергию будет иметь диск через 5 с после начала действия силы?
Дано:
Найти: Решение
Согласно второму закону Ньютона импульс силы равен
или
где
Выразим из (2) скорость вращения диска:
Кинетическая энергия вращения диска равна:
где
Угловая скорость находится по формуле:
Подставим в формулу (4) формулы (3), (5) и (6), получим:
ЗАДАЧА № II.70 Медный шар радиусом 10 см вращается с частотой 2 об/с вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вдвое?
Дано:
Найти: Решение
Работа по увеличению угловой скорости вращения шара будет равна приращению его кинетической энергии
Кинетическая энергия вращения шара в начальный момент времени равна:
где
Кинетическая энергия вращения шара в конечный момент времени равна:
По условию задачи
Подставим (5) в (4), получим
Подставим в формулу (1) формулы (2) и (6)
Угловая скорость связана с частотой формулой
Масса шара равна:
где Объем шара находится по формуле:
Подставим в (3) формулы (9) и (10), получим:
Подставим формулы (8) и (11) в формулу (7), после преобразований получим:
ЗАДАЧА № II.71 На скамье Жуковского сидит человек и держит в вытянутых руках гири по 10 кг каждая. Расстояние от каждой гири до оси вращения скамьи 50 см. Скамья вращается с частотой 1 с-1. Как изменится частота вращения скамьи и какую работу произведёт человек, если он сожмёт руки так, что расстояние от каждой гири до оси уменьшится до 20 см? Суммарный момент инерции человека и скамьи относительно оси вращения 2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи. Дано:
Найти: Решение
Частота вращения скамьи Жуковского изменяется в результате действий, производимых человеком при сближении гирь. (Предполагается, что человек не движется относительно скамьи). Однако и характер движения гирь, и характер взаимодействия гирь с человеком, и человека со скамьёй очень сложны. В системе тел скамья-человек-гири все эти силы являются внутренними и не изменяют ни импульса, ни момента импульса системы. Поскольку все тела системы совершают чисто вращательное движение вокруг одной и той же неподвижной оси, очевидно, следует рассматривать только момент импульса системы. При перемещении гирь относительно оси вращения на систему скамья-человек-гири действуют внешние силы: силы реакции оси (линия действия которых проходит через ось); сила тяжести и сила нормальной реакции, параллельные оси вращения. Моменты всех этих внешних сил относительно вертикальной оси вращения скамьи равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими). Следовательно, момент импульса этой системы остаётся постоянным:
где
Перепишем уравнение (1) в виде:
До сближения гирь момент инерции всей системы:
После сближения
Выразим угловые скорости
Подставим формулы (5), (3) и (4) в уравнение (2), получим:
Выразим из формулы (6) частоту вращения скамьи
Определим работу, которую совершит человек. Она будет равна изменению кинетической энергии системы:
Учтём, что
Подставим формулы (3),(4) и (5) в формулу (8), после ряда преобразований получим:
ЗАДАЧА № II.72 Выведите формулу для момента инерции полого шара относительно оси, проходящей через его центр. Масса шара равна
Дано: Найти: Решение
Момент инерции полого шара, определим по формуле:
где
Подставим формулу (2) в формулу (1), получим:
Обозначим через
ЗАДАЧА № II.73 Доска массой
Дано: Найти: Решение
Под действием силы
Часть силы, обеспечивающая поступательное движение доски:
Катки вращаются относительно осей, лежащих на земле и перпендикулярных силе
где Для определения момента инерции катка относительно оси
Произведём в формуле (2), соответствующие замены, получим:
Сила, обеспечивающая движение второго катка, будет такой же. Следовательно,
Ускорение движения доски, выразим из формулы (5):
ЗАДАЧА № II.74 Определите момент инерции
Дано:
Найти: 1) Решение
Для определения момента инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его конец используем теорему Штейнера:
где
Произведём, соответствующие замены в формуле (1), получим:
Для определения момента инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через точку
где
ЗАДАЧА № II.75 Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от неё. Скорость цилиндра до удара о стену 1,4 м/с, после удара – 1 м/с. Определить выделившееся при ударе количество теплоты.
Дано:
Найти: Решение
Количество теплоты, выделившееся при ударе, определим по формуле:
где Запишем формулу для нахождения кинетической энергии тела, катящегося по плоскости без скольжения в общем виде:
где
До удара:
После удара:
где Подставим формулы (3) и (4) в формулу (1), после преобразований, получим:
ЗАДАЧА № II.76 Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии согласно уравнению
Дано:
Найти: Решение Для нахождения момента сил, используем основной закон динамики вращательного движения:
где
Угловое ускорение шара определяется как
где
По условию задачи
Подставим формулу (5) в формулу (3), получим:
Формулы (6) и (2), подставим в формулу (1):
ЗАДАЧА № II.77 Горизонтальная платформа массой 25 кг и радиусом 0,8 м, вращается с частотой 18 мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определите частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5 кг∙м2 до 1 кг∙м2.
Дано:
Найти: Решение Момент импульса материальной точки, определяется по формуле:
где Для замкнутой системы
где Произведём в формуле (2) соответствующие замены, получим:
Выразим из формулы (3) частоту вращения платформы:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.009 с.) |

 , (II.58)
, (II.58)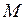 - момент силы, действующей на тело в течение времени
- момент силы, действующей на тело в течение времени  ;
; - момент инерции тела;
- момент инерции тела;  - угловая скорость;
- угловая скорость; - момент импульса.
- момент импульса. ; (II.59)
; (II.59) , (II.60)
, (II.60) - угловое ускорение.
- угловое ускорение. , (II.61)
, (II.61) , (II.62)
, (II.62)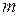 - масса точки;
- масса точки;  - линейная скорость точки;
- линейная скорость точки; 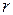 - расстояние точки от оси, относительно которой определяется момент импульса.
- расстояние точки от оси, относительно которой определяется момент импульса. , (II.63)
, (II.63) - плечо (кратчайшее расстояние от оси вращения до линии действия силы
- плечо (кратчайшее расстояние от оси вращения до линии действия силы 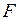 , или
, или (II.64)
(II.64)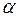 - угол между направлением действия силы и радиус – вектором
- угол между направлением действия силы и радиус – вектором  , проведённым от оси вращения к точке приложения силы.
, проведённым от оси вращения к точке приложения силы. ; (II.65)
; (II.65) , (II.66)
, (II.66) - расстояние элемента массы
- расстояние элемента массы  от оси вращения. То же в интегральной форме
от оси вращения. То же в интегральной форме . (II.67)
. (II.67)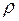 одинакова по всему объёму, то
одинакова по всему объёму, то  и
и , (II.68)
, (II.68)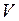 ;
; , (II.69)
, (II.69) - момент инерции тела относительно произвольной оси;
- момент инерции тела относительно произвольной оси; - момента инерции тела относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси;
- момента инерции тела относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси; - расстояние между осями.
- расстояние между осями. , (II.70)
, (II.70) - момент
- момент 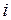 - того импульса тела, входящего в состав системы;
- того импульса тела, входящего в состав системы; , (II.71)
, (II.71) - угол поворота тела.
- угол поворота тела. . (II.72)
. (II.72) . (II.73)
. (II.73) , (II.74)
, (II.74) - кинетическая энергия поступательного движения тела;
- кинетическая энергия поступательного движения тела; - кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
- кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции. . (II.75)
. (II.75) проходит через точку, лежащую на линии соприкосновения катушки со столом)?
проходит через точку, лежащую на линии соприкосновения катушки со столом)?
 ,
, 
 по часовой стрелке, и она покатится направо. Момент силы
по часовой стрелке, и она покатится направо. Момент силы  . При приложении силы к кузову автомобиля плечо равно радиусу колеса, так как сила, приложенная к кузову, фактически действует на ось колеса.
. При приложении силы к кузову автомобиля плечо равно радиусу колеса, так как сила, приложенная к кузову, фактически действует на ось колеса. , где
, где  - вектор момента количества движения;
- вектор момента количества движения;  - момент силы, действующей на тело. В рассматриваемом случае момент силы, действующей на планету (рассчитанный относительно Солнца),
- момент силы, действующей на тело. В рассматриваемом случае момент силы, действующей на планету (рассчитанный относительно Солнца),  , где
, где  - сила тяготения, действующая со стороны Солнца на планету. Так как векторы
- сила тяготения, действующая со стороны Солнца на планету. Так как векторы  и, следовательно,
и, следовательно,  . Это утверждение справедливо для всех движений под действием центральных сил.
. Это утверждение справедливо для всех движений под действием центральных сил.
 определяется выражением:
определяется выражением:  ?
? и
и  кг;
кг; кг.
кг. -?
-?
 , (1)
, (1)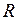 - радиус вала.
- радиус вала. , (2)
, (2) . (3)
. (3) , (4)
, (4)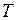 - сила натяжения шнура.
- сила натяжения шнура. ) и сила натяжения шнура (
) и сила натяжения шнура ( ).
).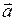 ) совпадает с направлением оси
) совпадает с направлением оси  .
. . (5)
. (5)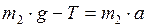 . (6)
. (6) . (7)
. (7) . (8)
. (8) ;
;  м/с2.
м/с2. 5 кг;
5 кг; 19,6 Н;
19,6 Н; 5 с.
5 с. -?
-? ,
, , (1)
, (1) и
и  - начальные значения времени и скорости. По условию задачи
- начальные значения времени и скорости. По условию задачи  и
и  , значит, из (1) следует, что
, значит, из (1) следует, что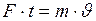 . (2)
. (2) . (3)
. (3) , (4)
, (4) . (5)
. (5) . (6)
. (6) ;
;  Дж.
Дж. см
см 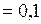 м;
м; об/с;
об/с;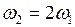 ;
; кг/м3.
кг/м3. -?
-? . (1)
. (1) , (2)
, (2) . (3)
. (3) . (4)
. (4) . (6)
. (6)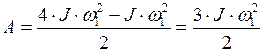 . (7)
. (7) . (8)
. (8) , (9)
, (9) - плотность меди.
- плотность меди. . (10)
. (10) . (11)
. (11) ;
;  Дж.
Дж. см =
см = 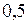 м;
м; см =
см =  м;
м; кг;
кг;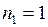 с-1;
с-1; кг·м2.
кг·м2. -?
-? 
 , (1)
, (1) - момент импульса системы до сближения гирь;
- момент импульса системы до сближения гирь; - момент импульса системы после сближения гирь.
- момент импульса системы после сближения гирь. . (2)
. (2) . (3)
. (3) . (4)
. (4) и
и  через частоту вращения
через частоту вращения  и
и  ;
;  . (5)
. (5)
 . (6)
. (6) ;
;  с-1.
с-1. . (7)
. (7) , получим:
, получим: . (8)
. (8) ;
;  Дж.
Дж.
 , (1)
, (1) ;
;  (2)
(2) . (3)
. (3) , получим:
, получим: .
.

 . (1)
. (1) , (2)
, (2) - момент той части силы, которая обеспечивает качение катков. Она равна:
- момент той части силы, которая обеспечивает качение катков. Она равна:  ;
;  - момент инерции катков;
- момент инерции катков;  - угловое ускорение.
- угловое ускорение. (3)
(3) . Выразим из полученного равенства силу
. Выразим из полученного равенства силу  . (4)
. (4) . (5)
. (5) .
.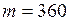 г
г  кг;
кг; см
см  м.
м.
 2)
2) 

 .
. - расстояние между осями.
- расстояние между осями. ;
;  кг · м2.
кг · м2. , теорема Штейнера будет иметь вид:
, теорема Штейнера будет иметь вид: , (2)
, (2) . Подставим его значение и значение
. Подставим его значение и значение  ;
;  кг · м2.
кг · м2.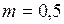 кг;
кг; м/с;
м/с; м/с.
м/с.
 , (1)
, (1) - кинетическая энергия тела, катящегося по плоскости без скольжения до удара;
- кинетическая энергия тела, катящегося по плоскости без скольжения до удара;  - кинетическая энергия тела, катящегося по плоскости без скольжения после удара;
- кинетическая энергия тела, катящегося по плоскости без скольжения после удара;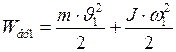 . (3)
. (3) , (4)
, (4) , а
, а  ;
;  .
. ;
;  Дж.
Дж. (
( рад/с2,
рад/с2,  рад/с3). Определите момент сил
рад/с3). Определите момент сил  кг;
кг;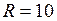 см;
см;
 , (3)
, (3) . (4)
. (4) . (5)
. (5) . (6)
. (6) ;
;  Н∙м.
Н∙м. кг;
кг; м;
м; мин-1
мин-1  с-1;
с-1; кг∙м2;
кг∙м2; кг∙м2.
кг∙м2.
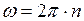 , где
, где  - частота вращения диска.
- частота вращения диска. . Тогда уравнение (1), можно будет переписать в виде:
. Тогда уравнение (1), можно будет переписать в виде: , (2)
, (2) и
и  - момент инерции человека.
- момент инерции человека. . (3)
. (3) ;
;  мин -1.
мин -1.


